What Is The Value Of X 70 35
faraar
Sep 07, 2025 · 6 min read
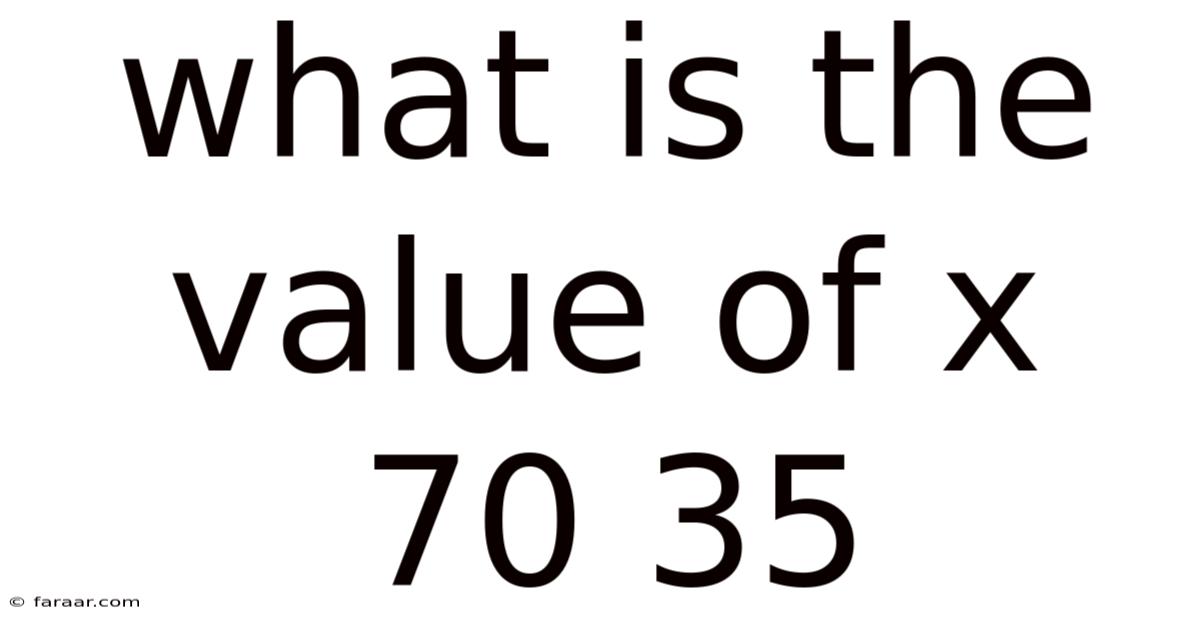
Table of Contents
Decoding the Equation: Finding the Value of x in "70 = 35x"
This article explores how to solve the simple algebraic equation 70 = 35x, explaining the process step-by-step and delving into the underlying mathematical concepts. Understanding this seemingly straightforward equation is fundamental to grasping more complex algebraic problems. We'll cover the basic principles of solving for 'x', provide practical examples, and even address some frequently asked questions. By the end, you'll not only know the value of x but also understand the logic behind finding it. This guide is designed for beginners, but even those with some algebraic experience might find it a helpful refresher.
Understanding the Equation: 70 = 35x
The equation 70 = 35x is a linear equation, meaning the highest power of the variable x is 1. It represents a simple relationship between two numbers: 70 and 35. The 'x' represents an unknown value that, when multiplied by 35, equals 70. Our goal is to isolate 'x' and find its numerical value. This involves applying basic algebraic principles.
Step-by-Step Solution: Isolating x
Solving for x involves manipulating the equation to get x by itself on one side of the equals sign. Here's how we do it:
-
Identify the Operation: Observe that 35 is being multiplied by x.
-
Perform the Inverse Operation: To isolate x, we need to perform the inverse operation of multiplication, which is division. We'll divide both sides of the equation by 35. This maintains the equality of the equation, a fundamental principle in algebra.
-
Applying the Division:
70 = 35x
70/35 = 35x/35
-
Simplifying:
2 = x
Therefore, the value of x is 2.
Verification: Checking Your Answer
It's always a good practice to verify your solution. Substitute the value of x (which we found to be 2) back into the original equation:
70 = 35 * 2
70 = 70
Since the equation holds true, our solution (x = 2) is correct.
Expanding the Concept: Different Forms of Linear Equations
While the equation 70 = 35x is straightforward, let's expand our understanding to include other forms of similar linear equations. These variations involve different arrangements of the numbers and the variable:
-
35x = 70: This is simply a reversed version of the original equation. The solution process remains the same; divide both sides by 35 to get x = 2.
-
70 - 35x = 0: This equation requires an extra step. First, add 35x to both sides: 70 = 35x. Then, proceed as before, dividing both sides by 35 to find x = 2.
-
70 = 35x + 0: This is essentially the same as the original equation, with an added term of zero which doesn't affect the outcome.
These examples highlight the flexibility of algebraic manipulation. Regardless of how the equation is initially presented, the fundamental principle of maintaining equality through inverse operations remains the core of the solution process.
The Importance of Understanding Variables
The concept of a variable, represented by x in our equation, is crucial in algebra. Variables allow us to represent unknown quantities and establish relationships between them. Without variables, expressing mathematical relationships and solving for unknowns would be impossible.
In our equation, x acts as a placeholder for a number. The beauty of algebra lies in its ability to find the value of this unknown number through methodical manipulation of the equation. This process of manipulating equations to isolate and solve for a variable is fundamental to all areas of mathematics, including calculus, statistics, and beyond.
Practical Applications: Where This Matters
Understanding how to solve simple linear equations like 70 = 35x isn't just an academic exercise. This type of problem solving has wide-ranging real-world applications. For example:
-
Ratio and Proportion Problems: If you know 35 items cost $70, you can use this equation to find the cost of one item.
-
Unit Conversion: Converting units like kilometers to miles or pounds to kilograms often involves solving similar equations.
-
Financial Calculations: Calculating interest, discounts, or profit margins often involves setting up and solving equations resembling this one.
-
Science and Engineering: In various fields of science and engineering, solving for an unknown variable is fundamental to numerous calculations and modeling.
These are just a few examples. The ability to solve simple algebraic equations is a foundational skill that opens doors to a deeper understanding of numerous subjects and allows for problem-solving in various aspects of life.
Further Exploration: More Complex Equations
While 70 = 35x is a basic equation, it lays the groundwork for solving more complex linear equations. Consider these examples:
-
2x + 5 = 11: This involves multiple steps: first, subtract 5 from both sides, then divide by 2 to solve for x.
-
3x - 7 = 14: Similar to the above, this requires adding 7 to both sides before dividing by 3.
-
ax + b = c: This introduces general constants a, b, and c. Solving involves subtracting b from both sides and then dividing by a. This emphasizes the generalizability of algebraic methods.
These more complex examples build upon the foundational principles demonstrated in solving 70 = 35x. The same core concepts – maintaining equality, using inverse operations – apply, but with additional steps to isolate the variable.
Frequently Asked Questions (FAQ)
Q: What if the equation was 35 = 70x?
A: This is simply the reciprocal of our original equation. You would still divide both sides by 70, resulting in x = 0.5 or 1/2.
Q: Why is dividing both sides by 35 a valid operation?
A: Dividing both sides of an equation by the same non-zero number maintains the equality. This is a fundamental property of equations. It's like balancing a scale; if you remove equal weight from both sides, the scale remains balanced.
Q: Can I multiply both sides by a number instead of dividing?
A: You could, but in this case, it wouldn't be as efficient. Multiplying both sides would introduce fractions, making the simplification more complicated. However, in other equations, multiplication might be a necessary step.
Q: What if I get a negative value for x?
A: That's perfectly acceptable. Negative numbers are valid solutions in algebra.
Conclusion: Mastering the Fundamentals
Solving the equation 70 = 35x, while seemingly simple, represents a crucial step in understanding algebra. This article has not only provided the solution (x = 2) but also explored the underlying mathematical principles, demonstrated practical applications, and touched upon more complex scenarios. By mastering these fundamental concepts, you build a solid foundation for tackling more challenging mathematical problems in the future. Remember that consistent practice is key to solidifying your understanding and building confidence in your algebraic abilities. So, keep practicing, and you'll be solving even more complex equations in no time!
Latest Posts
Latest Posts
-
What Are The Units Of Potential Energy
Sep 07, 2025
-
Learn How To Spell For Adults
Sep 07, 2025
-
What Is The Distance Between 6 8 And 3 9
Sep 07, 2025
-
How Many Valence Electrons Does Palladium Have
Sep 07, 2025
-
What Is An Example Of A Qualitative Observation
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of X 70 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.