If A Number Is An Integer Then It Is Rational
faraar
Sep 07, 2025 · 6 min read
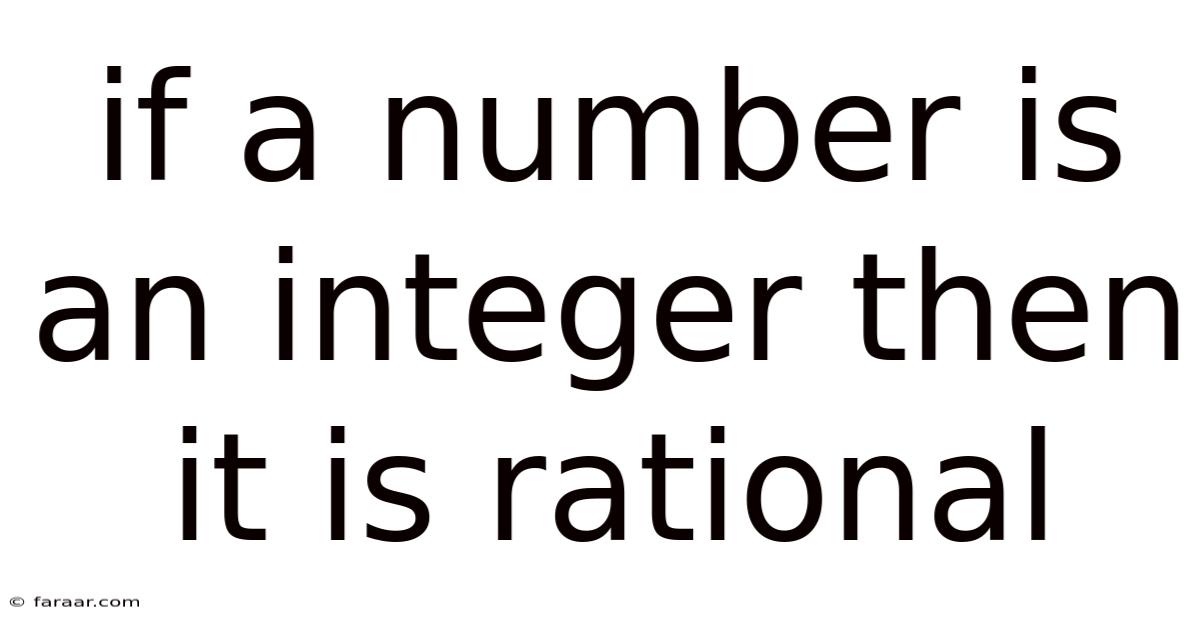
Table of Contents
If a Number is an Integer, Then it is Rational: A Deep Dive into Number Systems
This article explores the fundamental relationship between integers and rational numbers. We'll delve into the definitions of both, prove the statement "If a number is an integer, then it is rational," and address common misconceptions. Understanding this connection is crucial for building a solid foundation in mathematics, particularly in algebra, calculus, and number theory. This article is designed for students and anyone seeking a clearer understanding of number systems.
Understanding Integers
Integers are the set of whole numbers and their negative counterparts. This includes positive numbers like 1, 2, 3..., negative numbers like -1, -2, -3..., and zero (0). We represent the set of integers using the symbol ℤ. Therefore:
ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}
Integers are used extensively in everyday life for counting, representing quantities, and performing calculations. They form the basis for more complex number systems. It's important to remember that integers do not include fractions or decimals.
Understanding Rational Numbers
Rational numbers are numbers that can be expressed as the quotient or fraction p/q, where p and q are integers, and q is not equal to zero (q ≠ 0). This is because division by zero is undefined. The set of rational numbers is denoted by ℚ.
Examples of rational numbers include:
- 1/2 (one-half)
- 3/4 (three-quarters)
- -2/5 (negative two-fifths)
- 7 (which can be expressed as 7/1)
- 0 (which can be expressed as 0/1)
Notice that integers are also included in the set of rational numbers. Any integer can be expressed as a fraction with a denominator of 1. This is the key to understanding the relationship between integers and rational numbers.
Proving the Statement: If a Number is an Integer, Then it is Rational
The statement "If a number is an integer, then it is rational" is a direct consequence of the definitions of integers and rational numbers. We can prove this using a direct proof:
1. Assume: Let 'n' be an arbitrary integer. This means 'n' belongs to the set ℤ.
2. Express 'n' as a fraction: We can express any integer 'n' as a fraction by placing it over 1: n/1.
3. Check the definition of a rational number: The expression n/1 satisfies the definition of a rational number because:
- 'n' is an integer (our initial assumption).
- '1' is an integer.
- '1' is not equal to zero (1 ≠ 0).
4. Conclusion: Since 'n' can be expressed as a fraction n/1 that meets all criteria for a rational number, we conclude that 'n' is a rational number. Therefore, if a number is an integer, it is also a rational number.
Visual Representation
Imagine a Venn diagram. The circle representing the set of integers (ℤ) is completely contained within the larger circle representing the set of rational numbers (ℚ). This visually demonstrates that all integers are also rational numbers, but not all rational numbers are integers. The rational numbers include the integers and a vast array of fractions and decimals that can be expressed in the form p/q.
Common Misconceptions
Several misconceptions often arise when discussing integers and rational numbers:
-
Misconception 1: All rational numbers are integers. This is incorrect. Many rational numbers are fractions or decimals that cannot be expressed as whole numbers (e.g., 1/2, 0.75).
-
Misconception 2: Irrational numbers are a subset of rational numbers. This is false. Irrational numbers, such as π (pi) and √2 (the square root of 2), cannot be expressed as a fraction p/q, where p and q are integers and q ≠ 0. They lie outside the set of rational numbers.
-
Misconception 3: Zero is not a rational number. This is incorrect. Zero (0) can be expressed as 0/1, fulfilling the definition of a rational number.
-
Misconception 4: Repeating decimals are not rational. This is incorrect. Repeating decimals can always be expressed as fractions, making them rational numbers. For example, 0.333... (one-third) is equivalent to 1/3.
Illustrative Examples
Let's solidify our understanding with a few examples:
-
Example 1: The number 5 is an integer. It can be expressed as 5/1, which satisfies the definition of a rational number.
-
Example 2: The number -12 is an integer. It can be expressed as -12/1, which is a rational number.
-
Example 3: The number 0 is an integer. It can be expressed as 0/1, fulfilling the requirement for a rational number.
-
Example 4: The number 1/3 is a rational number but not an integer. It's a fraction that cannot be simplified to a whole number.
-
Example 5: The number √2 (approximately 1.414) is not a rational number; it's an irrational number. It cannot be expressed as a fraction of two integers.
The Importance of Understanding Number Systems
Understanding the distinctions and relationships between different number systems like integers and rational numbers is crucial for mathematical advancement. This understanding allows us to:
-
Perform accurate calculations: Knowing the properties of integers and rational numbers helps in performing mathematical operations correctly.
-
Solve equations and inequalities: The properties of number systems are fundamental to solving algebraic problems.
-
Work with more complex mathematical concepts: The foundation laid by understanding integers and rational numbers is essential for grasping more advanced concepts such as real numbers, complex numbers, and set theory.
Frequently Asked Questions (FAQ)
Q1: Are all rational numbers integers?
A1: No, all integers are rational numbers, but not all rational numbers are integers. Rational numbers encompass integers and fractions.
Q2: Can you provide an example of a number that is rational but not an integer?
A2: 1/2 (one-half) is a classic example. It's a rational number (it can be expressed as a fraction), but it's not a whole number, thus not an integer.
Q3: What is the difference between rational and irrational numbers?
A3: Rational numbers can be expressed as the fraction p/q where p and q are integers and q≠0. Irrational numbers cannot be expressed in this form; they have non-repeating, non-terminating decimal expansions (e.g., π, √2).
Q4: Is 0.5 a rational number?
A4: Yes, 0.5 is a rational number because it can be expressed as the fraction 1/2.
Q5: How can I determine if a decimal is a rational number?
A5: If the decimal terminates (ends) or repeats in a pattern, it is a rational number. If it neither terminates nor repeats, it's irrational.
Conclusion
The statement "If a number is an integer, then it is rational" is fundamentally true and forms a cornerstone in our understanding of number systems. This article has clarified the definitions of integers and rational numbers, provided a formal proof of the statement, addressed common misconceptions, and highlighted the importance of grasping these concepts in furthering your mathematical journey. Remember that integers are a subset of rational numbers – every integer can be represented as a rational number, but not every rational number is an integer. This understanding is essential for continued success in mathematics.
Latest Posts
Latest Posts
-
Singing Teachers For Adults Near Me
Sep 08, 2025
-
5 Is One Fourth Of A Number C
Sep 08, 2025
-
How Are An Atoms Chemical Properties Determined
Sep 08, 2025
-
Calculate The Energy Of A Photon Emitted When An Electron
Sep 08, 2025
-
Difference Between Es And Esta In Spanish
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about If A Number Is An Integer Then It Is Rational . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.