5 Is One-fourth Of A Number C .
faraar
Sep 08, 2025 · 4 min read
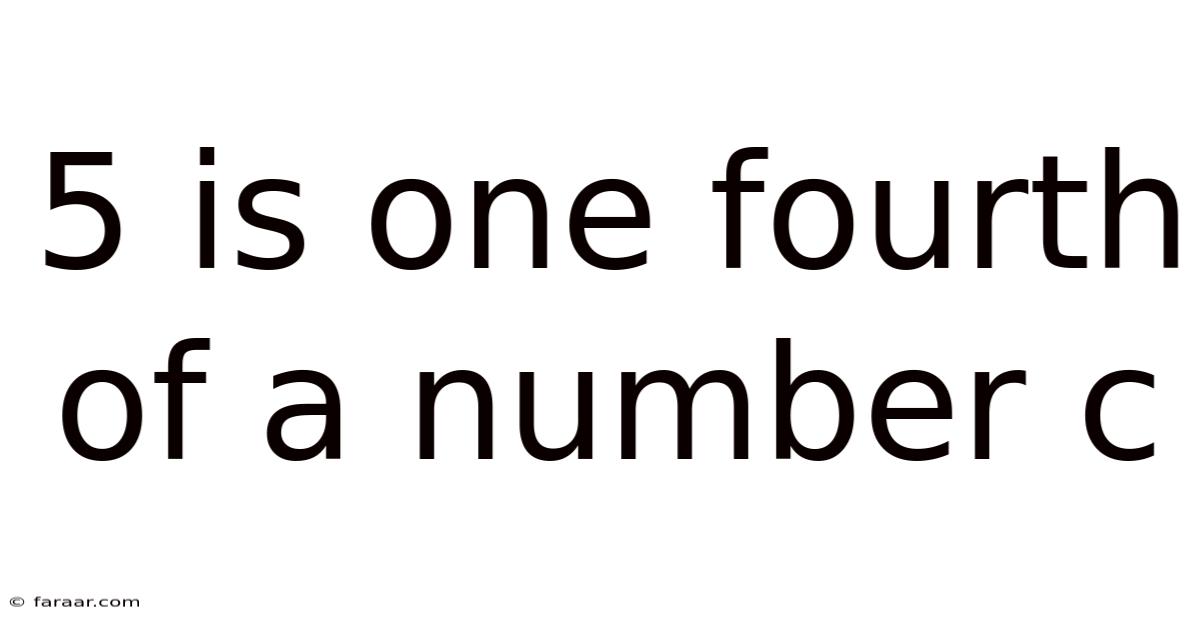
Table of Contents
5 is One-Fourth of a Number c: Unlocking the Power of Algebraic Equations
This article explores the seemingly simple equation: 5 is one-fourth of a number c. We'll dissect this problem, explaining how to solve it step-by-step, delving into the underlying mathematical principles, and providing a deeper understanding of algebraic equations. This will not only help you solve this specific problem but equip you with the skills to tackle similar algebraic challenges with confidence.
Understanding the Problem: Translating Words into Math
The phrase "5 is one-fourth of a number c" might seem intimidating at first glance, but it's essentially a concise way of expressing a mathematical relationship. Let's break it down:
- "5 is": This translates directly to the equals sign (=). We have 5 on one side of the equation.
- "one-fourth": This means 1/4 or 0.25. This is the fractional part of the number c.
- "of a number c ": This indicates multiplication. "Of" in mathematical language usually translates to multiplication. So, "one-fourth of a number c" means (1/4) * c or 0.25 * c.
Putting it all together, the sentence "5 is one-fourth of a number c" becomes the algebraic equation:
5 = (1/4) * c or equivalently 5 = 0.25 * c
Solving the Equation: Step-by-Step Guide
Now that we've translated the word problem into an algebraic equation, we can solve for the unknown variable c. The goal is to isolate c on one side of the equation. Here's how:
Step 1: Eliminate the fraction (or decimal). To make the equation simpler, we can eliminate the fraction (1/4) by multiplying both sides of the equation by its reciprocal, which is 4:
4 * 5 = 4 * (1/4) * c
This simplifies to:
20 = c
Alternatively, if you used the decimal form:
4 * 5 = 4 * 0.25 * c
This also simplifies to:
20 = c
Step 2: Verify the solution. Always check your answer by substituting it back into the original equation:
5 = (1/4) * 20
5 = 5
The equation holds true, confirming that our solution is correct. Therefore, the number c is 20.
Deeper Dive: Understanding Algebraic Principles
This seemingly simple problem showcases several fundamental algebraic principles:
- Variables: The letter c represents an unknown value, called a variable. Algebra allows us to solve for these unknowns.
- Equations: An equation shows the equality between two expressions. Solving an equation involves manipulating it to isolate the variable.
- Inverse Operations: To isolate the variable, we use inverse operations. Multiplication and division are inverse operations, as are addition and subtraction. In our example, we used multiplication (multiplying by 4) to undo the division (dividing by 4) that was implicitly present in the original equation.
- Properties of Equality: The process of solving equations relies on the properties of equality. These properties state that you can perform the same operation on both sides of an equation without changing the equality. For instance, we multiplied both sides of the equation by 4.
Expanding the Concept: Variations and Applications
The core concept of solving for an unknown value based on a fractional relationship has far-reaching applications:
- Percentage Problems: Many percentage problems can be modeled using similar equations. For example, "30% of a number is 15" can be written as 0.3 * x = 15, which can be solved similarly to our original problem.
- Ratio and Proportion Problems: Ratios and proportions often involve solving equations with fractions. For example, if the ratio of boys to girls in a class is 2:3 and there are 10 boys, how many girls are there? This can be set up as a proportion and solved algebraically.
- Real-world Applications: From calculating discounts and taxes to determining ingredient ratios in recipes or scaling architectural designs, the ability to solve equations like this is essential in numerous real-world scenarios.
Frequently Asked Questions (FAQ)
-
What if the fraction was different? The process remains the same. You would simply multiply both sides of the equation by the reciprocal of the fraction. For example, if the problem was "5 is two-thirds of a number c", you would multiply both sides by 3/2.
-
What if the equation was more complex? More complex equations might involve multiple steps and operations. Remember to follow the order of operations (PEMDAS/BODMAS) and use inverse operations to isolate the variable.
-
Can I use a calculator? Absolutely! Calculators can help with the arithmetic, especially with more complex equations. However, understanding the underlying principles is crucial.
-
Why is verifying the solution important? Verifying your answer ensures that you've solved the equation correctly. It's a good habit to develop in all areas of mathematics.
Conclusion: Mastering Algebraic Equations
Solving the equation "5 is one-fourth of a number c" might seem trivial at first. However, understanding the process reveals the fundamental building blocks of algebra. Through this step-by-step approach, we've not only found the solution (c = 20) but also explored the deeper mathematical concepts behind it. This knowledge empowers you to tackle more complex algebraic problems with confidence, opening doors to a wider range of mathematical applications and problem-solving abilities. Remember, practice is key. The more you work with these equations, the more comfortable and proficient you’ll become. So, grab a pen and paper, and start exploring the exciting world of algebra!
Latest Posts
Latest Posts
-
How To Solve Fraction Word Problems
Sep 08, 2025
-
How To Find Slope In Standard Form
Sep 08, 2025
-
How Many Inches Are In 7 Yards
Sep 08, 2025
-
Find The Perimeter Of The Polygon With The Given Vertices
Sep 08, 2025
-
What Must Citizens Do When Subjected To Despotism
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 5 Is One-fourth Of A Number C . . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.