How To Solve 2x 3y 12
faraar
Sep 22, 2025 · 6 min read
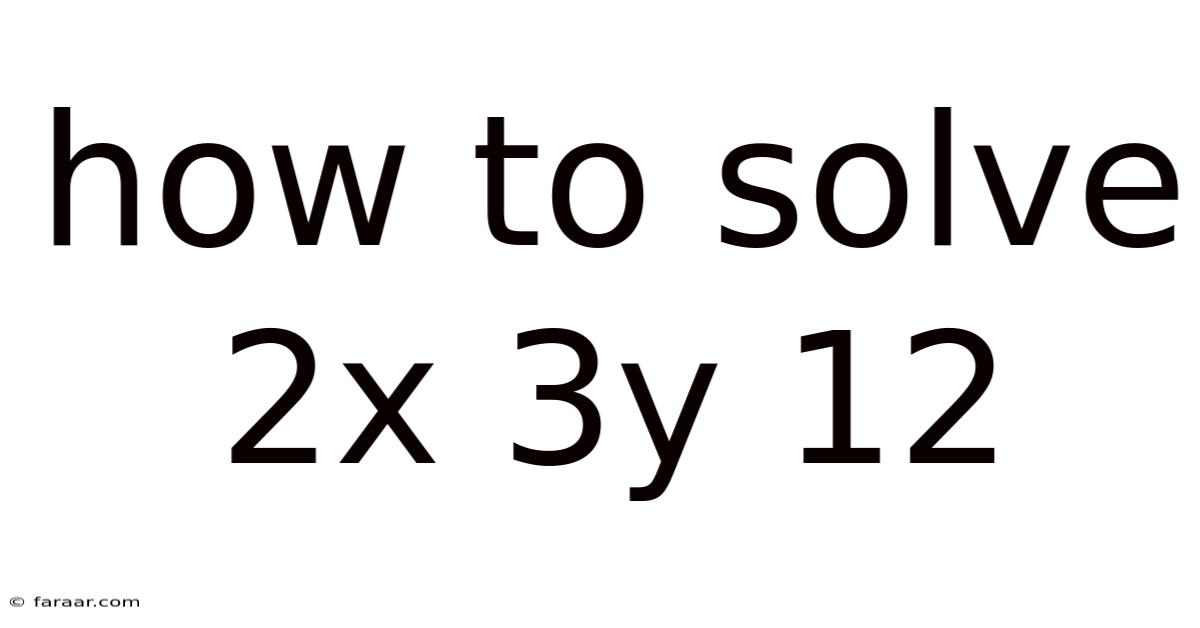
Table of Contents
Solving the Equation 2x + 3y = 12: A Comprehensive Guide
This article provides a thorough explanation of how to solve the linear equation 2x + 3y = 12. We'll explore various methods, including graphing, substitution, and elimination, demonstrating each technique step-by-step. Understanding how to solve this type of equation is fundamental to algebra and has wide-ranging applications in various fields. We will also delve into the underlying mathematical concepts and address frequently asked questions.
Introduction: Understanding Linear Equations
A linear equation is an algebraic equation of the form ax + by = c, where 'a', 'b', and 'c' are constants, and 'x' and 'y' are variables. The equation 2x + 3y = 12 is a linear equation in two variables. Solving this equation means finding the values of 'x' and 'y' that satisfy the equation, meaning when substituted, they make the equation true. Because we have two variables and only one equation, there are infinitely many solutions. We'll explore ways to represent this infinite solution set.
Method 1: Graphing the Equation
One way to visualize the solutions of 2x + 3y = 12 is by graphing it. To do this, we need to find at least two points that satisfy the equation. We can do this by setting one variable to zero and solving for the other.
-
Finding the x-intercept: Let y = 0. Then 2x + 3(0) = 12, which simplifies to 2x = 12. Dividing both sides by 2, we get x = 6. So one point is (6, 0).
-
Finding the y-intercept: Let x = 0. Then 2(0) + 3y = 12, which simplifies to 3y = 12. Dividing both sides by 3, we get y = 4. So another point is (0, 4).
Now, plot these two points (6,0) and (0,4) on a coordinate plane. Draw a straight line through these points. Every point on this line represents a solution to the equation 2x + 3y = 12. This graphical representation showcases the infinite number of solutions.
Method 2: Solving Using the Substitution Method
The substitution method involves solving for one variable in terms of the other and then substituting that expression into the equation. Let's solve for 'x':
-
Solve for x: Start with the equation 2x + 3y = 12. Subtract 3y from both sides: 2x = 12 - 3y. Then divide both sides by 2: x = 6 - (3/2)y.
-
Substitute: This expression for 'x' can now be substituted into any equation (in this case, we only have one). However, the result will remain the same. Since we only have one equation, we cannot find specific values for x and y. What we have achieved is expressing x in terms of y.
-
Solution Set: The solution set is represented by the ordered pairs (6 - (3/2)y, y), where 'y' can be any real number. This confirms that there are infinitely many solutions. For instance, if y = 2, then x = 6 - (3/2)(2) = 3. Thus, (3, 2) is a solution. If y = 0, then x = 6, giving us the point (6, 0), as we found earlier through graphing.
Method 3: Solving Using the Elimination Method
The elimination method, also known as the addition method, aims to eliminate one variable by adding or subtracting the equations. Since we only have one equation, this method isn't directly applicable. The elimination method is most useful when dealing with a system of two or more linear equations. For example, if we had a second equation like x + y = 5, we could use elimination to solve for x and y.
Understanding the Solution Set: Infinite Solutions
The equation 2x + 3y = 12 represents a straight line on a coordinate plane. Every point on this line is a solution to the equation. Because there are infinitely many points on a line, there are infinitely many solutions to this equation. This is different from a system of two linear equations, which can have one unique solution, no solution (parallel lines), or infinitely many solutions (coincident lines).
Applications of Linear Equations
Linear equations like 2x + 3y = 12 are fundamental in many areas:
- Economics: Modeling supply and demand, calculating costs and profits.
- Physics: Representing relationships between physical quantities like velocity, distance, and time.
- Engineering: Solving problems in structural analysis, circuit design, and fluid mechanics.
- Computer Science: Used in algorithm design and optimization.
Extending the Concept: Systems of Linear Equations
As mentioned earlier, the elimination method is particularly useful when dealing with a system of linear equations. Let's consider the following system:
2x + 3y = 12 x + y = 5
To solve this system using elimination:
-
Multiply equations: Multiply the second equation by -2 to get -2x - 2y = -10.
-
Add equations: Add this modified equation to the first equation: (2x + 3y) + (-2x - 2y) = 12 + (-10). This simplifies to y = 2.
-
Substitute: Substitute y = 2 into either of the original equations (let's use x + y = 5). This gives x + 2 = 5, so x = 3.
The solution to this system is (3, 2). This demonstrates how a system of equations can lead to a unique solution unlike our single equation.
Frequently Asked Questions (FAQ)
-
Q: Can I solve for x and y separately in 2x + 3y = 12? A: No, you cannot find unique values for x and y with only one equation. You can express one variable in terms of the other, as shown in the substitution method, but you’ll have infinitely many solution pairs.
-
Q: What does it mean when an equation has infinitely many solutions? A: It means that there are countless pairs of x and y values that satisfy the equation. Graphically, this represents all points on a line.
-
Q: How can I check if a solution is correct? A: Substitute the values of x and y into the original equation (2x + 3y = 12). If the equation holds true (both sides are equal), the solution is correct. For example, using the point (3,2) gives 2(3) + 3(2) = 6 + 6 = 12.
Conclusion: Mastering Linear Equations
Solving the equation 2x + 3y = 12 might seem simple, but understanding its solution set and the different methods for representing it is crucial for a solid foundation in algebra. The concept extends to more complex systems of equations and has far-reaching implications in various fields. Mastering these techniques empowers you to tackle more advanced mathematical problems and opens doors to a deeper understanding of the world around us. Remember, practice is key to mastering these concepts. Continue to work through examples and explore different approaches to solidify your understanding. The ability to solve linear equations is a cornerstone of mathematical literacy, providing a valuable skill applicable to numerous aspects of life and future studies.
Latest Posts
Latest Posts
-
1 2 Divided By 3 4 In A Fraction
Sep 22, 2025
-
How Many Oranges In A Gallon Of Juice
Sep 22, 2025
-
How Many Bottles Of Water Equal 2 Liters
Sep 22, 2025
-
What Does Audentes Fortuna Iuvat Mean
Sep 22, 2025
-
The Oxygen Produced In Photosynthesis Comes From What Molecule
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about How To Solve 2x 3y 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.