How Many 2/3 Are In 1
faraar
Sep 17, 2025 · 6 min read
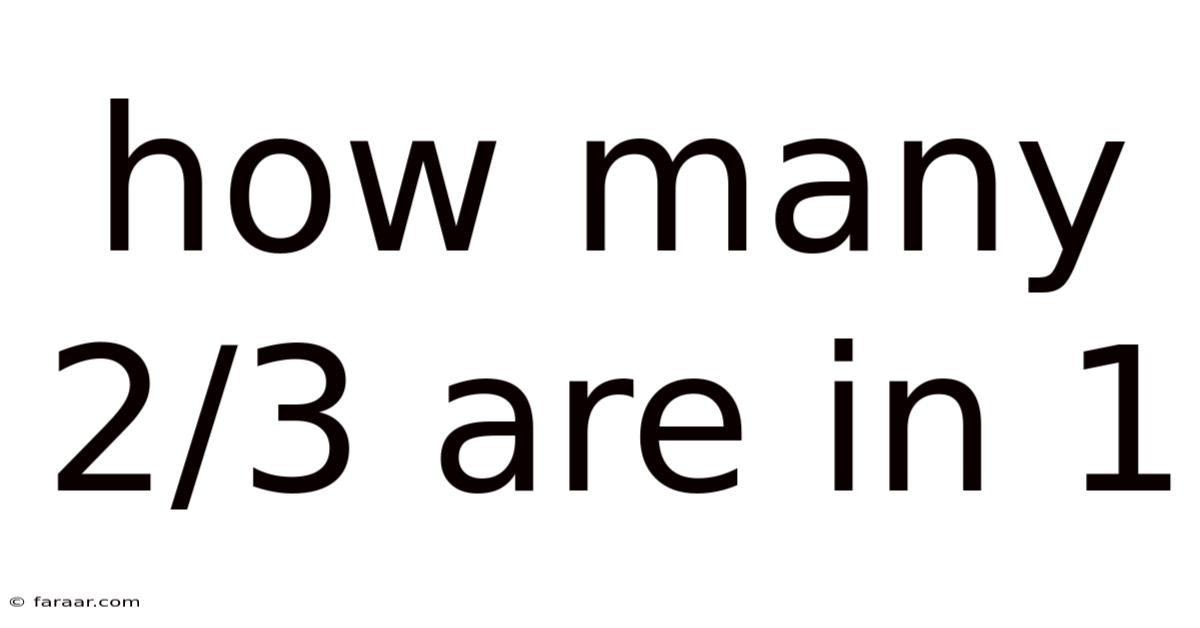
Table of Contents
How Many 2/3 Are in 1? Unpacking Fractions and Division
This seemingly simple question, "How many 2/3 are in 1?", opens a door to a deeper understanding of fractions, division, and the reciprocal relationship between them. It's a fundamental concept in mathematics that underpins more advanced topics, and mastering it provides a strong foundation for future learning. This article will explore this question in detail, providing multiple approaches to solving it, explaining the underlying principles, and addressing frequently asked questions. We'll move beyond simply stating the answer and delve into the why behind the solution, ensuring a comprehensive understanding.
Introduction: Understanding Fractions and Division
Before diving into the specific problem, let's refresh our understanding of fractions and division. A fraction, like 2/3, represents a part of a whole. The numerator (2) indicates the number of parts we have, and the denominator (3) indicates the total number of equal parts the whole is divided into. Division, on the other hand, is the process of splitting a quantity into equal groups. The question "How many 2/3 are in 1?" essentially asks how many times the fraction 2/3 fits into the whole number 1.
Method 1: Visual Representation
One of the easiest ways to understand this is through a visual representation. Imagine a single whole object, like a pizza. To find out how many 2/3 are in 1, we need to divide this pizza into thirds. Each third represents 1/3 of the whole pizza. Now, how many of these 1/3 slices would we need to make up 2/3? The answer is two, naturally. Since we're trying to determine how many sets of 2/3 fit into a whole, we see that a whole (1) is composed of one and a half sets of 2/3.
Therefore, we have 1 and a half sets of 2/3 in 1 whole pizza. This visual representation makes it intuitive to see that the answer is not a whole number. Let's formalize this with mathematical methods.
Method 2: Inverting and Multiplying
This method utilizes the concept of reciprocals. The reciprocal of a fraction is obtained by switching the numerator and denominator. The reciprocal of 2/3 is 3/2. To find how many 2/3 are in 1, we can multiply 1 by the reciprocal of 2/3:
1 × (3/2) = 3/2
This result, 3/2, is an improper fraction (where the numerator is larger than the denominator). Converting it to a mixed number, we get 1 ½. This confirms our visual representation: there are 1 ½ sets of 2/3 in 1.
This method showcases the fundamental relationship between division and multiplication with fractions. Dividing by a fraction is equivalent to multiplying by its reciprocal.
Method 3: Using Division Directly
We can also approach this problem directly using division. We want to find how many 2/3 are in 1, which can be expressed as the division problem:
1 ÷ (2/3)
Remember that dividing by a fraction is the same as multiplying by its reciprocal. So:
1 ÷ (2/3) = 1 × (3/2) = 3/2 = 1 ½
Again, the answer is 1 ½. This approach emphasizes the direct application of division rules for fractions.
Method 4: Understanding the Concept of "How Many" in Fraction Division
The question "How many 2/3 are in 1?" asks for the number of times 2/3 fits into 1. We can think of this as a division problem:
- Dividend: 1 (the whole we're dividing)
- Divisor: 2/3 (the fraction we're dividing by)
- Quotient: The result, representing the number of times the divisor goes into the dividend.
When dividing fractions, we always multiply the dividend by the reciprocal of the divisor. This leads us back to the same solution:
1 * (3/2) = 3/2 = 1 ½
This method highlights the conceptual interpretation of the division problem within the context of fractions.
The Significance of 1 ½: Beyond a Simple Answer
The answer 1 ½ might seem counterintuitive at first. We're used to whole numbers when dealing with "how many," but fractions allow for more nuanced answers. The 1 ½ signifies that one full set of 2/3 is contained within 1, and there's an additional half of another 2/3 remaining. It emphasizes the idea that fractions represent parts of a whole and that the number of times a fraction fits into another number doesn't always result in a whole number.
Extending the Concept: How Many 2/3 Are in Other Numbers?
Let's extend this concept to other whole numbers. How many 2/3 are in 2? We can use the same principles:
2 ÷ (2/3) = 2 × (3/2) = 6/2 = 3
There are 3 sets of 2/3 in 2. Notice how multiplying by the reciprocal simplifies the calculation.
Let's try another example: How many 2/3 are in 5?
5 ÷ (2/3) = 5 × (3/2) = 15/2 = 7 ½
This demonstrates the consistent application of the method across different whole numbers.
Addressing Frequently Asked Questions (FAQs)
Q: Why do we invert and multiply when dividing fractions?
A: Inverting and multiplying is a shortcut derived from the rules of division. When dividing by a fraction, we're essentially asking how many times the divisor fits into the dividend. Multiplying by the reciprocal effectively performs this operation efficiently.
Q: Can this concept be applied to decimals?
A: Absolutely! The fraction 2/3 is equivalent to the repeating decimal 0.666... You can apply the same division principles using decimals, but working with fractions often leads to cleaner and more precise results.
Q: What if the question was "How many 1/3 are in 1?"
A: In this case, we'd have:
1 ÷ (1/3) = 1 × 3/1 = 3
There are 3 sets of 1/3 in 1. This is a more straightforward case where the whole number is directly divisible by the fraction.
Q: What if the whole number was a fraction itself?
A: The same principles apply. For example, to find how many 2/3 are in ½:
(1/2) ÷ (2/3) = (1/2) × (3/2) = 3/4
There are 3/4 of a set of 2/3 in ½. The method remains consistent.
Conclusion: Mastering Fractions and Division
Understanding how many 2/3 are in 1 is more than just solving a single problem. It's about grasping the fundamental relationship between fractions and division. By mastering this concept, you build a stronger foundation for more advanced mathematical concepts. Remember the key takeaway: dividing by a fraction is equivalent to multiplying by its reciprocal. This simple yet powerful rule unlocks a wealth of problem-solving possibilities in the world of fractions and beyond. Through various methods—visual representation, inverting and multiplying, direct division, and conceptual understanding—we’ve explored this seemingly simple question in depth, showcasing its importance in building a solid mathematical foundation. This understanding will serve as a strong base for tackling more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
4x 2y 8 In Slope Intercept Form
Sep 17, 2025
-
3 Less Than Twice A Number
Sep 17, 2025
-
Are Diagonals Of A Parallelogram Perpendicular
Sep 17, 2025
-
When Fissionable Mass Tips Into Chain Reaction Crossword
Sep 17, 2025
-
How To Find X Intercept Y Mx B
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about How Many 2/3 Are In 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.