3 Less Than Twice A Number
faraar
Sep 17, 2025 · 6 min read
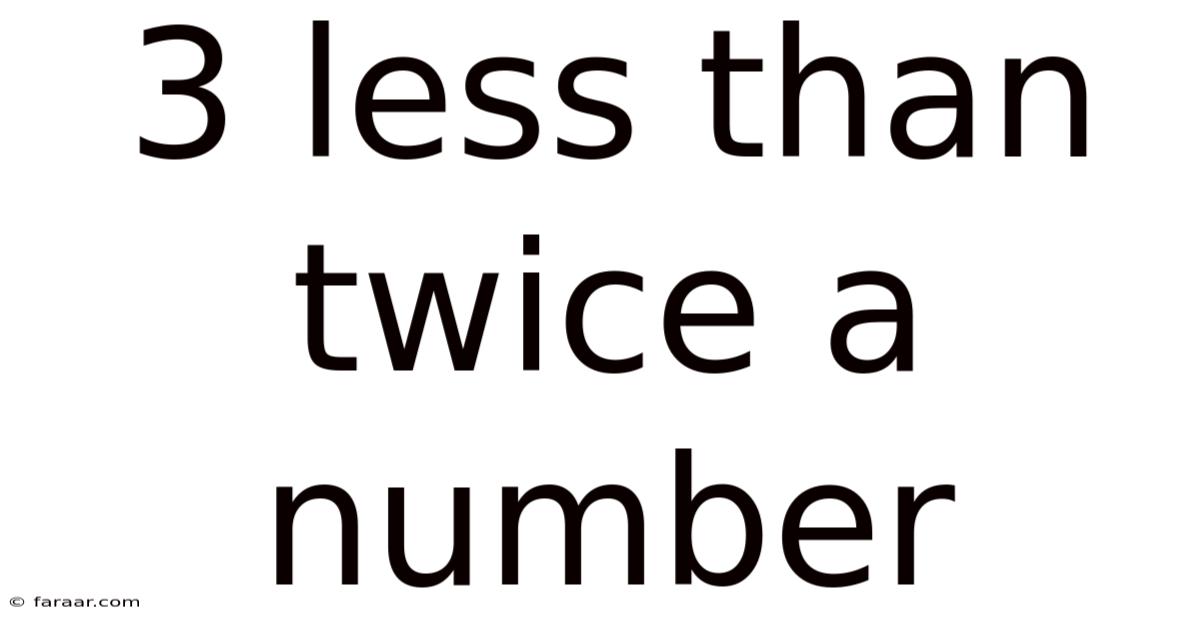
Table of Contents
Decoding "3 Less Than Twice a Number": A Comprehensive Guide to Algebraic Expressions
Understanding algebraic expressions is a fundamental skill in mathematics. This seemingly simple phrase, "3 less than twice a number," introduces crucial concepts like variables, coefficients, and the order of operations. This article will delve deep into the meaning, applications, and nuances of this expression, providing a comprehensive guide suitable for learners of all levels. We will explore how to translate the phrase into an algebraic expression, solve related equations, and explore real-world applications, ultimately equipping you with a strong understanding of this core mathematical concept.
Understanding the Components: Numbers, Variables, and Operations
Before we tackle "3 less than twice a number," let's break down the individual components. The phrase involves several key mathematical elements:
-
A Number: This represents an unknown quantity, which we typically represent with a variable, usually x or n. This is the foundation of the expression, the subject of our algebraic manipulation.
-
Twice a Number: This means multiplying the number (our variable) by 2. Mathematically, this is represented as 2x or 2n. The '2' is the coefficient, a numerical multiplier of the variable.
-
3 Less Than: This indicates subtraction. We are taking 3 away from the result of "twice a number." The '3' is a constant, a fixed numerical value.
-
Order of Operations: The order in which we perform these operations is crucial. Multiplication (twice a number) comes before subtraction (3 less than). This is governed by the standard order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction).
Translating the Phrase into an Algebraic Expression
Now, let's combine these components to translate "3 less than twice a number" into a concise algebraic expression:
2x - 3 (or 2n - 3 if you prefer using 'n' as the variable)
This expression accurately captures the meaning of the phrase. It states that we first multiply the unknown number (x) by 2 and then subtract 3 from the result.
Solving Equations Involving "3 Less Than Twice a Number"
The expression "2x - 3" is just a starting point. We often encounter this expression within equations where we need to solve for the unknown number (x). Let's explore some examples:
Example 1: Finding the Number
If "3 less than twice a number is 7," we can write this as an equation:
2x - 3 = 7
To solve for x, we follow these steps:
-
Add 3 to both sides: This isolates the term with x. The equation becomes: 2x = 10
-
Divide both sides by 2: This solves for x. The solution is: x = 5
Therefore, the number is 5.
Example 2: A More Complex Equation
Let's consider a more complex scenario: "Twice a number, decreased by 3, is equal to the number increased by 5." We can translate this into an equation:
2x - 3 = x + 5
Solving this equation involves:
-
Subtract x from both sides: This simplifies the equation to: x - 3 = 5
-
Add 3 to both sides: This isolates x: x = 8
Thus, the number is 8.
Example 3: Involving Inequalities
The expression can also appear in inequalities. For example, "3 less than twice a number is greater than 11" translates to:
2x - 3 > 11
Solving this inequality follows a similar process:
-
Add 3 to both sides: 2x > 14
-
Divide both sides by 2: x > 7
This means the number is greater than 7.
Real-World Applications
The seemingly simple expression "3 less than twice a number" has surprisingly diverse real-world applications. Here are a few examples:
-
Geometry: Consider the relationship between the length and width of a rectangle. If the length is "3 less than twice the width," we can represent this using the expression 2w - 3, where w is the width. This allows us to solve problems involving the area or perimeter of the rectangle.
-
Finance: Imagine a scenario where you earn twice your previous hourly wage minus a $3 deduction for taxes. The expression 2h - 3, where h is your previous hourly wage, models your current earnings.
-
Physics: In physics, many formulas involve linear relationships, which can be expressed using similar algebraic expressions. For instance, the distance traveled at a constant speed after a certain time, subtracting a delay of 3 units, could be modeled by such an equation.
-
Everyday Problems: Imagine you have a number of apples, and your friend takes twice that number minus three apples. You can use the expression to calculate how many apples your friend took.
A Deeper Dive into the Mathematical Concepts
The expression "3 less than twice a number" highlights several important mathematical concepts:
-
Variables and Constants: The expression clearly distinguishes between variables (the unknown number) and constants (the numbers 2 and 3). This distinction is crucial in algebra and beyond.
-
Coefficients: The '2' in '2x' is a coefficient, indicating the scale factor applied to the variable. Understanding coefficients is critical in understanding the behavior and relationships in equations.
-
Order of Operations: The order in which operations are performed (multiplication before subtraction) emphasizes the importance of adhering to the standard rules of mathematical order.
-
Linear Equations: The resulting equations often fall into the category of linear equations, characterized by a straight line when graphed. This opens the door to further exploration of linear algebra and its applications.
-
Solving Equations and Inequalities: The process of solving equations and inequalities associated with this expression demonstrates fundamental algebraic techniques, including manipulating equations to isolate the unknown variable.
Frequently Asked Questions (FAQs)
Q1: What if the phrase was "Twice a number less than 3"?
This would change the order of operations significantly. The expression becomes 3 - 2x. This is a fundamentally different expression that will result in different answers when used in equations.
Q2: Can I use different variables instead of x or n?
Absolutely! You can use any letter or symbol to represent the unknown number as long as you define it clearly. For example, you could use 'a', 'y', or even a descriptive variable like 'apples'.
Q3: What if the number '3' is negative?
If the phrase was "3 more than twice a number", the expression would be 2x + 3. If it was "Negative 3 less than twice a number," the expression would be 2x - (-3) which simplifies to 2x + 3. Careful attention to the signs is crucial.
Conclusion
"3 less than twice a number" may seem like a simple phrase, but it encapsulates many fundamental algebraic concepts. Understanding how to translate this phrase into an algebraic expression, solve related equations, and interpret its real-world applications is crucial for mastering algebra. This seemingly straightforward expression serves as a foundational building block for more complex mathematical concepts and problems. By grasping the nuances of this expression, you build a strong foundation for future mathematical endeavors. Remember to always pay attention to the order of operations and the meaning of the words to ensure accurate translation and problem-solving. With practice, you'll become proficient in manipulating and applying this type of algebraic expression with confidence.
Latest Posts
Latest Posts
-
Value Of Notes In 6 8 Time Signature
Sep 17, 2025
-
What Layer Of The Earth Is Most Dense
Sep 17, 2025
-
How To Find The Slope Of A Demand Curve
Sep 17, 2025
-
How To Write 10 Page Paper
Sep 17, 2025
-
How To Find A Reference Number
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 Less Than Twice A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.