How Many 1/4 Make 1/3 Cup Of Water
faraar
Sep 12, 2025 · 6 min read
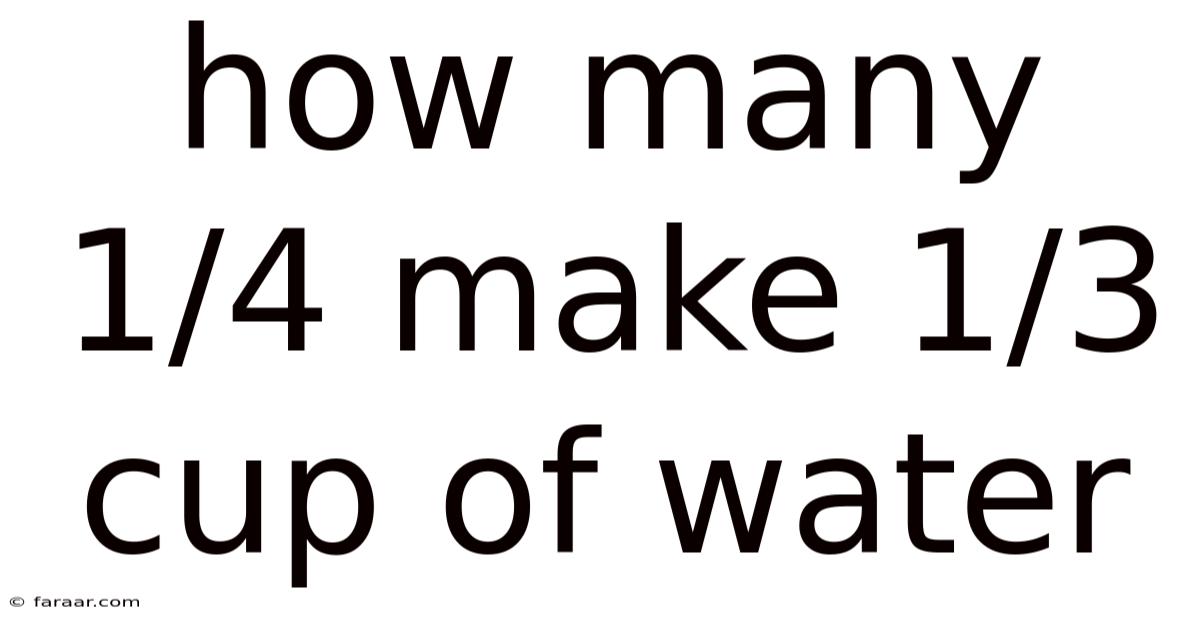
Table of Contents
How Many 1/4 Cups Make 1/3 Cup of Water? A Deep Dive into Fractions and Measurement
This seemingly simple question – how many 1/4 cups make 1/3 cup of water – actually opens a door to a deeper understanding of fractions, measurement conversion, and practical application in everyday cooking and baking. While a quick calculation might suffice, exploring the underlying principles helps solidify mathematical concepts and improves our ability to tackle more complex problems involving ratios and proportions. This article will guide you through the solution, exploring the different approaches, and delve into the related concepts to provide a comprehensive understanding.
Understanding the Problem: Fractions and Measurement
The core of the problem lies in understanding the relationship between fractions. We're dealing with two different fractional units: 1/4 cup and 1/3 cup. The question asks us to determine how many times 1/4 cup fits into 1/3 cup. This translates into a division problem: (1/3) ÷ (1/4). Let's approach this problem using several methods.
Method 1: Direct Division of Fractions
The most straightforward method involves directly dividing the two fractions. Remember that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 1/4 is 4/1 or simply 4.
Therefore:
(1/3) ÷ (1/4) = (1/3) x (4/1) = 4/3
This means that 4/3 of a 1/4 cup is needed to make 1/3 cup of water. As a mixed number, 4/3 equals 1 and 1/3. So, you need one full 1/4 cup and 1/3 of another 1/4 cup to make 1/3 cup.
Method 2: Finding a Common Denominator
Another approach involves finding a common denominator for the two fractions. The least common multiple of 3 and 4 is 12. We can rewrite the fractions with a denominator of 12:
1/3 = 4/12 1/4 = 3/12
Now, the problem becomes: (4/12) ÷ (3/12). Notice that the denominators are the same, so we can simply divide the numerators:
4 ÷ 3 = 4/3
This again gives us the same answer: 4/3 or 1 and 1/3. This method highlights the importance of equivalent fractions in simplifying calculations.
Method 3: Visual Representation
Visualizing the problem can provide a more intuitive understanding. Imagine a pie chart divided into 12 equal slices. 1/3 of the pie represents 4 slices (4/12), and 1/4 of the pie represents 3 slices (3/12). The question becomes: how many sets of 3 slices are there in 4 slices? Again, the answer is 4/3, or 1 and 1/3 sets.
Method 4: Using Decimal Equivalents
Converting the fractions to decimals can also help.
1/3 ≈ 0.333 1/4 = 0.25
Dividing the decimal equivalents:
0.333 ÷ 0.25 ≈ 1.333
This approximation confirms our previous result of 1 and 1/3. However, it's important to note that using decimal approximations can sometimes introduce slight inaccuracies, especially when dealing with repeating decimals.
Practical Applications and Measurement Considerations
In a real-world kitchen scenario, obtaining precisely 1/3 of a 1/4 cup might be challenging. You would likely need to estimate. Measuring cups often come with markings for 1/4 cup, 1/3 cup, and 1/2 cup, but rarely for more granular divisions.
The fact that we get a result of 1 and 1/3 highlights the limitations of directly translating fractions into practical measurements. It's a reminder that while mathematical calculations provide exact answers, real-world application might necessitate approximations and adjustments.
Understanding the Significance of the Result: 4/3 Cups
The answer 4/3, or 1 and 1/3, emphasizes the importance of understanding fractional relationships. It demonstrates that sometimes, the result of a fraction operation isn't a whole number. This is a common occurrence in mathematics and is crucial to grasp when working with ratios, proportions, and various measurements. It also helps in understanding the concept of 'more than one but less than two', which is a crucial skill for understanding quantities in many contexts.
Expanding on the Concept: Working with Different Unit Fractions
This problem can be extended to work with different unit fractions. For example, let's say we want to determine how many 1/8 cups make 1/3 cup. We would use the same approach:
(1/3) ÷ (1/8) = (1/3) x (8/1) = 8/3 = 2 and 2/3
This illustrates that the method remains consistent even when the unit fractions change. The core concept of dividing fractions using reciprocals remains the same.
Frequently Asked Questions (FAQ)
- Q: Can I use a different measuring unit, like milliliters?
A: Yes, you can certainly convert the cup measurements to milliliters. However, the underlying principle of dividing fractions will remain the same. You would need to determine the equivalent of 1/4 cup and 1/3 cup in milliliters first and then perform the division.
- Q: Is there a simpler way to solve this problem without using fractions?
A: While the use of fractions is inherent to the problem, simplifying it without resorting to fractions directly is difficult. Decimal conversions offer a way to approach the problem without explicitly writing fractions but it may introduce some degree of approximation and error.
- Q: What if I need to determine how many 1/3 cups make 1/4 cup?
A: In that case, you'd reverse the division: (1/4) ÷ (1/3) = (1/4) x (3/1) = 3/4. This shows the importance of identifying which fraction is the dividend and which is the divisor.
- Q: Why is it important to understand this concept?
A: Understanding fractional relationships and measurement conversions is crucial in many aspects of life, from cooking and baking to engineering and construction. It is a fundamental skill needed for problem-solving in various mathematical and real-world scenarios.
Conclusion: Mastering Fractions for Everyday Life
This exploration of "How many 1/4 cups make 1/3 cup of water?" goes beyond a simple arithmetic problem. It reinforces the fundamental principles of fraction operations, measurement conversions, and the application of mathematical concepts in everyday scenarios. Mastering these skills not only enhances our ability to tackle similar problems but also cultivates a deeper understanding of fundamental mathematical principles and their real-world implications. The ability to accurately handle fractions and proportions is a valuable asset in many fields, and understanding how to approach this seemingly simple problem offers a strong foundation for tackling more complex mathematical challenges. Remember to always consider the context and choose the most appropriate method for solving the problem at hand.
Latest Posts
Latest Posts
-
Circle Inscribed In An Isosceles Triangle
Sep 12, 2025
-
Dilation Of 3 2 About The Origin
Sep 12, 2025
-
Rewrite Expression Without Absolute Value Bars
Sep 12, 2025
-
What Is The Fraction Of 4 5
Sep 12, 2025
-
What Is Objective Theory Of Contracts
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/4 Make 1/3 Cup Of Water . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.