What Is The Fraction Of 4/5
faraar
Sep 12, 2025 · 6 min read
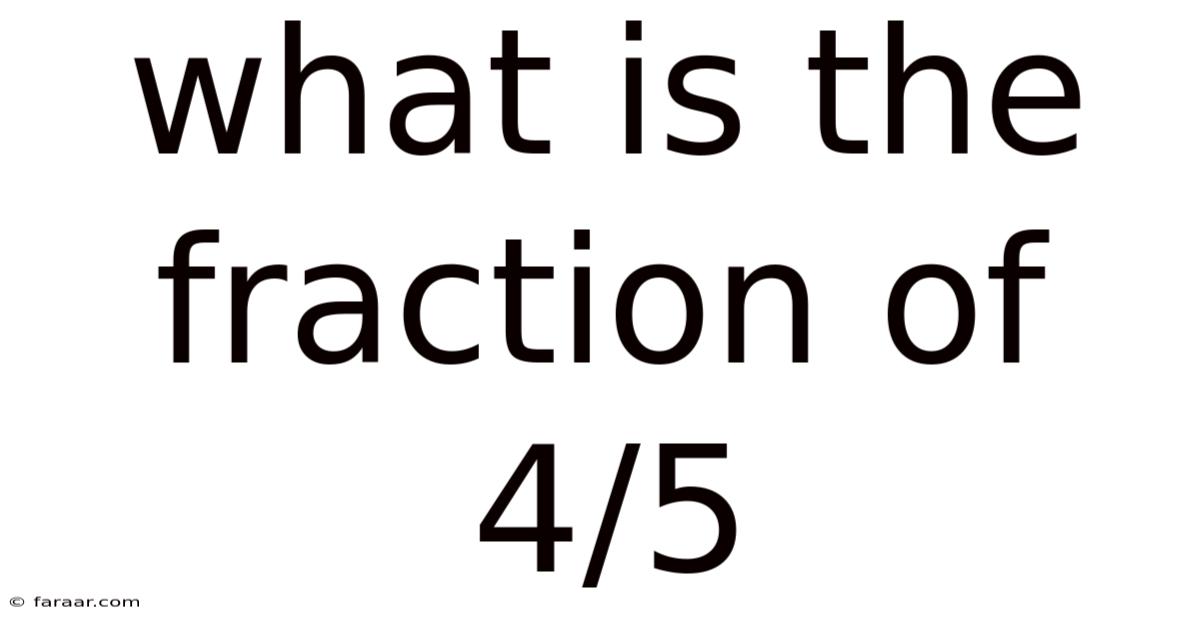
Table of Contents
What is the Fraction 4/5? A Deep Dive into Fractions and Their Applications
Understanding fractions is fundamental to grasping mathematical concepts, from basic arithmetic to advanced calculus. This article will delve into the fraction 4/5, exploring its meaning, representation, equivalent fractions, operations involving it, and its real-world applications. By the end, you'll not only know what 4/5 represents but also possess a much deeper understanding of fractions themselves.
Introduction: Deconstructing the Fraction 4/5
The fraction 4/5 is a way of expressing a part of a whole. It's a representation of a ratio, where 4 represents the numerator (the part we're interested in) and 5 represents the denominator (the total number of equal parts the whole is divided into). In simpler terms, imagine a pizza cut into 5 equal slices. 4/5 means you have 4 out of those 5 slices. This seemingly simple fraction has far-reaching implications across various fields.
Visualizing 4/5: Different Representations
Fractions can be visualized in several ways, making them more intuitive and easier to understand.
-
Using Shapes: Imagine a circle divided into 5 equal parts. Shading 4 of those parts visually represents the fraction 4/5. This is effective for beginners. The same principle applies to squares, rectangles, or any shape divided into equal parts.
-
Using Number Lines: A number line can be divided into fifths. Locate the point that corresponds to 4/5, which will lie between 0 and 1, closer to 1. This method helps in comparing fractions.
-
Using Decimal Representation: The fraction 4/5 can be easily converted to a decimal by dividing the numerator (4) by the denominator (5). This results in 0.8. This decimal equivalent provides an alternative representation and is frequently used in practical applications.
-
Using Percentages: To express 4/5 as a percentage, multiply the decimal equivalent (0.8) by 100%. This gives us 80%. This representation is particularly useful for expressing proportions in everyday contexts.
Equivalent Fractions: Exploring Different Forms of 4/5
An important concept in understanding fractions is the idea of equivalent fractions. These are fractions that represent the same value even though they look different. You can obtain equivalent fractions by multiplying or dividing both the numerator and the denominator by the same number (excluding zero).
For example, multiplying both the numerator and denominator of 4/5 by 2 gives us 8/10. Similarly, multiplying by 3 gives 12/15, and multiplying by 4 gives 16/20. All these fractions (4/5, 8/10, 12/15, 16/20, etc.) are equivalent to each other. This concept is vital for simplifying fractions and performing operations with them.
Simplifying Fractions: Reducing 4/5 to its Lowest Terms
Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. In the case of 4/5, this is already in its simplest form because 4 and 5 have no common factors other than 1. However, understanding the process is crucial. To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it.
Operations with 4/5: Addition, Subtraction, Multiplication, and Division
Let's explore how to perform basic arithmetic operations using 4/5:
-
Addition: To add 4/5 to another fraction, you need a common denominator. For example, adding 4/5 + 1/5 = 5/5 = 1. Adding 4/5 + 1/2 requires finding a common denominator (10): 8/10 + 5/10 = 13/10 = 1 3/10
-
Subtraction: Similar to addition, subtraction requires a common denominator. For example, 4/5 - 1/5 = 3/5. Subtracting 4/5 - 1/2 requires finding a common denominator (10): 8/10 - 5/10 = 3/10.
-
Multiplication: Multiplying fractions is relatively straightforward: multiply the numerators together and multiply the denominators together. For example, 4/5 * 2/3 = (4 * 2) / (5 * 3) = 8/15.
-
Division: To divide fractions, invert the second fraction (reciprocal) and multiply. For example, 4/5 ÷ 2/3 = 4/5 * 3/2 = 12/10 = 6/5 = 1 1/5.
Real-World Applications of 4/5: Everyday Examples
The fraction 4/5 appears in many real-world situations:
-
Shopping: If a store offers a 20% discount, that's equivalent to 1/5 off. So, if an item costs $5, the discount is $1 (1/5 of $5). The price after the discount would be $4 (4/5 of the original price).
-
Cooking: A recipe might call for 4/5 of a cup of flour. This requires understanding and accurate measurement.
-
Measurement: Many projects involve measurements where fractions are used. For instance, 4/5 of a meter or 4/5 of an inch are common measurements encountered in various tasks.
-
Probability: The probability of a certain event might be expressed as 4/5, meaning the event is likely to occur.
-
Data Analysis: In statistics, data analysis frequently uses fractions to represent proportions and relative frequencies. 4/5 might represent 80% of a survey population responding positively to a particular question.
Comparing Fractions: Is 4/5 Bigger or Smaller Than Other Fractions?
Comparing fractions involves understanding their relative sizes. To compare 4/5 with another fraction, you can:
-
Convert to Decimals: Converting both fractions to decimals makes comparison easier. For instance, comparing 4/5 (0.8) with 3/4 (0.75) shows that 4/5 is larger.
-
Find a Common Denominator: If you're comparing 4/5 with 7/10, find a common denominator (10). 4/5 becomes 8/10, making the comparison simple: 8/10 > 7/10.
-
Visual Representation: Visualizing the fractions using shapes or a number line can aid in comparison.
Improper Fractions and Mixed Numbers: Expanding the Understanding
While 4/5 is a proper fraction (numerator < denominator), it's important to understand improper fractions (numerator ≥ denominator) and mixed numbers (a whole number and a proper fraction). An improper fraction can be converted to a mixed number and vice versa. For example, 6/5 is an improper fraction, which is equivalent to the mixed number 1 1/5.
Frequently Asked Questions (FAQ)
Q: What is 4/5 as a decimal?
A: 4/5 as a decimal is 0.8.
Q: What is 4/5 as a percentage?
A: 4/5 as a percentage is 80%.
Q: How do I simplify 4/5?
A: 4/5 is already in its simplest form.
Q: What is the reciprocal of 4/5?
A: The reciprocal of 4/5 is 5/4.
Q: Can 4/5 be expressed as a mixed number?
A: No, 4/5 is a proper fraction and cannot be expressed as a mixed number.
Conclusion: Mastering Fractions for a Brighter Future
Understanding fractions is crucial for success in mathematics and many other fields. This detailed exploration of the fraction 4/5 has not only explained its meaning but also provided a solid foundation in fraction concepts. Mastering these concepts empowers you to tackle more complex mathematical problems and confidently apply these skills to real-world scenarios. From understanding discounts in shopping to accurately following recipes, the practical applications of fractions are vast and significant. By continuing to practice and explore the world of fractions, you’ll unlock a deeper understanding of mathematics and its immense power.
Latest Posts
Latest Posts
-
What Is 60 Kilometers In Miles Per Hour
Sep 12, 2025
-
Can You Draw A Square That Is Not A Rhombus
Sep 12, 2025
-
The Smiths Took Out A 30 Year Mortgage
Sep 12, 2025
-
How To Find Tangent Line With Derivative
Sep 12, 2025
-
Check All Of The Solutions To The Original Equation
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Fraction Of 4/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.