How Do You Factor 2x 2 5x 3
faraar
Sep 04, 2025 · 6 min read
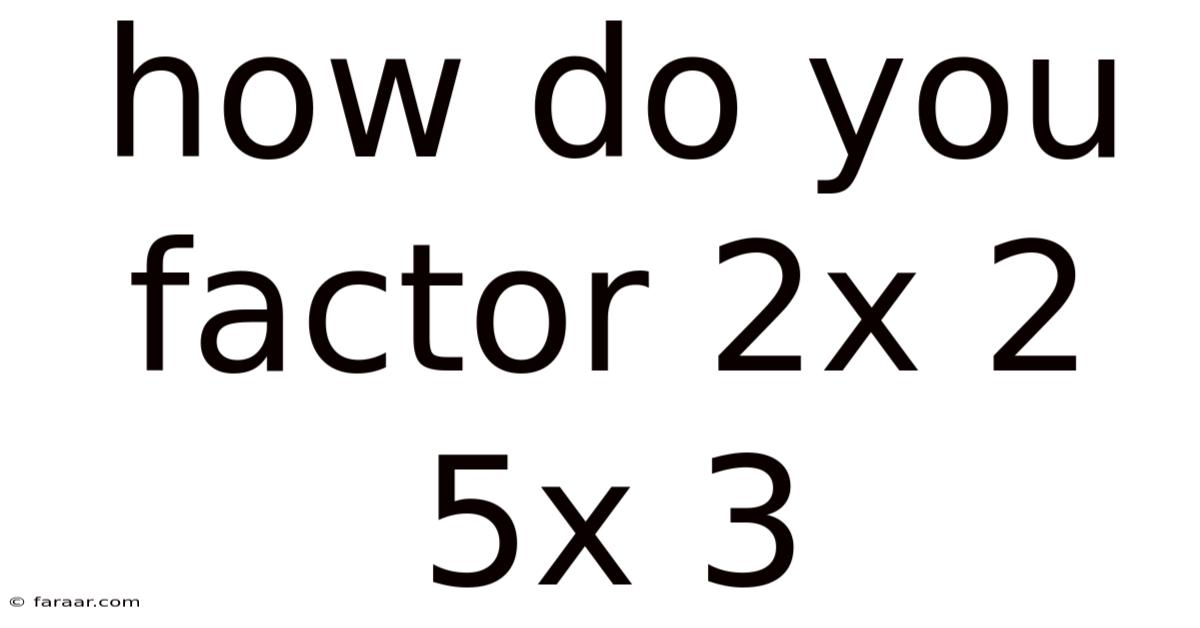
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into 2x² + 5x + 3
Factoring quadratic expressions is a fundamental skill in algebra. Understanding how to factor allows you to solve quadratic equations, simplify complex expressions, and gain a deeper understanding of mathematical relationships. This comprehensive guide will walk you through the process of factoring the quadratic expression 2x² + 5x + 3, explaining the steps, the underlying principles, and addressing common questions. We'll explore different methods and provide ample examples to solidify your understanding.
Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants. Our target expression, 2x² + 5x + 3, fits this form perfectly, with a = 2, b = 5, and c = 3. Factoring this expression means rewriting it as a product of two simpler expressions, usually two binomials.
Method 1: AC Method (for factoring quadratic expressions)
This method is particularly helpful when the coefficient of x² (the 'a' value) is not 1. Here's how to factor 2x² + 5x + 3 using the AC method:
-
Find the product AC: Multiply the coefficient of x² (a = 2) and the constant term (c = 3). This gives us AC = 2 * 3 = 6.
-
Find two numbers that add up to B and multiply to AC: We need two numbers that add up to the coefficient of x (b = 5) and multiply to 6. These numbers are 2 and 3 (2 + 3 = 5 and 2 * 3 = 6).
-
Rewrite the middle term: Rewrite the middle term (5x) using the two numbers we found: 2x and 3x. The expression becomes 2x² + 2x + 3x + 3.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
- (2x² + 2x) + (3x + 3)
- 2x(x + 1) + 3(x + 1)
-
Factor out the common binomial: Notice that both terms now share the binomial (x + 1). Factor this out:
- (x + 1)(2x + 3)
Therefore, the factored form of 2x² + 5x + 3 is (x + 1)(2x + 3).
Method 2: Trial and Error (for factoring quadratic expressions)
This method involves systematically trying different combinations of binomial factors until you find the one that works. It's often faster for simpler quadratics but can become more time-consuming for more complex expressions.
-
Set up the binomial factors: Since the leading coefficient is 2, we know the factors will be of the form (ax + c)(dx + e), where 'ad' equals 2 and 'ce' equals 3.
-
Consider the factors of the leading coefficient and the constant term: The factors of 2 are 1 and 2, and the factors of 3 are 1 and 3.
-
Test combinations: Let's try different combinations:
- (x + 1)(2x + 3): Expanding this gives 2x² + 3x + 2x + 3 = 2x² + 5x + 3. This is correct!
- (x + 3)(2x + 1): Expanding this gives 2x² + x + 6x + 3 = 2x² + 7x + 3. This is incorrect.
- (2x + 1)(x + 3): Expanding this gives 2x² + 6x + x + 3 = 2x² + 7x + 3. This is also incorrect.
- (2x + 3)(x + 1): Expanding this also gives 2x² + 5x + 3.
This illustrates that while multiple binomial pairs can exist, only certain combinations yield the correct expansion. The trial and error method reinforces the uniqueness of the correct factorization.
Method 3: Using the Quadratic Formula (to find the roots, then factor)
While not a direct factoring method, the quadratic formula can indirectly help us find the factors. The quadratic formula solves for the roots (or zeros) of a quadratic equation: x = [-b ± √(b² - 4ac)] / 2a.
-
Find the roots: Using the quadratic formula with a = 2, b = 5, and c = 3, we get:
- x = [-5 ± √(5² - 4 * 2 * 3)] / (2 * 2)
- x = [-5 ± √(25 - 24)] / 4
- x = [-5 ± 1] / 4
- x₁ = (-5 + 1) / 4 = -1
- x₂ = (-5 - 1) / 4 = -3/2
-
Use the roots to find the factors: If x₁ is a root, then (x - x₁) is a factor. Similarly, if x₂ is a root, then (x - x₂) is a factor. Therefore, the factors are (x - (-1)) = (x + 1) and (x - (-3/2)) = (x + 3/2).
-
Adjust for integer coefficients: To get integer coefficients, we can multiply the second factor by 2: 2(x + 3/2) = 2x + 3. This gives us the factors (x + 1)(2x + 3), which is consistent with our previous methods.
This method is particularly useful when the quadratic expression is difficult to factor directly using other methods. It provides a guaranteed way to find the roots and subsequently derive the factors.
Explanation of the Underlying Principles
The success of these methods relies on the distributive property of multiplication (often called FOIL - First, Outer, Inner, Last). When we expand (x + 1)(2x + 3), we get:
- First: x * 2x = 2x²
- Outer: x * 3 = 3x
- Inner: 1 * 2x = 2x
- Last: 1 * 3 = 3
Adding these together, we obtain 2x² + 5x + 3, confirming that (x + 1)(2x + 3) is the correct factorization. The AC method cleverly manipulates this process in reverse to find the factors.
Solving Quadratic Equations using Factoring
Once you've factored a quadratic expression, you can use it to solve the corresponding quadratic equation. For example, to solve 2x² + 5x + 3 = 0, we use the factored form (x + 1)(2x + 3) = 0. This equation is true if either (x + 1) = 0 or (2x + 3) = 0. Solving these gives us x = -1 and x = -3/2, which are the roots we found using the quadratic formula.
Frequently Asked Questions (FAQ)
- Q: What if the quadratic expression can't be factored easily?
A: If you can't find simple integer factors, the quadratic formula or completing the square are reliable alternatives. Some quadratic expressions are prime, meaning they cannot be factored into simpler expressions with integer coefficients.
- Q: Can I use any method I prefer?
A: Yes! Choose the method you find most comfortable and efficient. The AC method is generally reliable, while trial and error can be quicker for simpler expressions. The quadratic formula always works but may be more computationally intensive.
- Q: What if the coefficient of x² is negative?
A: Factor out a -1 first, then proceed with your chosen factoring method. For example, -2x² - 5x -3 would become -1(2x² + 5x + 3), making the factoring simpler.
- Q: Is there a way to check my answer?
A: Always expand your factored expression to verify that it equals the original quadratic expression. This is a crucial step to ensure the correctness of your solution.
Conclusion
Factoring quadratic expressions is a fundamental algebraic skill with wide-ranging applications. Mastering this technique will significantly enhance your ability to solve quadratic equations, simplify expressions, and tackle more advanced algebraic problems. While multiple methods exist, understanding the underlying principles and choosing the most suitable approach based on the complexity of the expression are key to success. Remember to always check your work by expanding the factored form to ensure it matches the original quadratic. Practice regularly, and you'll quickly gain proficiency in this important algebraic skill. The example of factoring 2x² + 5x + 3 provides a solid foundation for tackling more complex quadratic expressions in the future.
Latest Posts
Latest Posts
-
What Is Between 1 2 And 1 4
Sep 07, 2025
-
1 3 4 Cup Divided By 3
Sep 07, 2025
-
Which Quadratic Equation Models The Situation Correctly
Sep 07, 2025
-
Which Quarter Has The Smallest Spread Of Data
Sep 07, 2025
-
According To The Theory Of Evolution By Natural Selection
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about How Do You Factor 2x 2 5x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.