What Is Between 1/2 And 1/4
faraar
Sep 07, 2025 · 6 min read
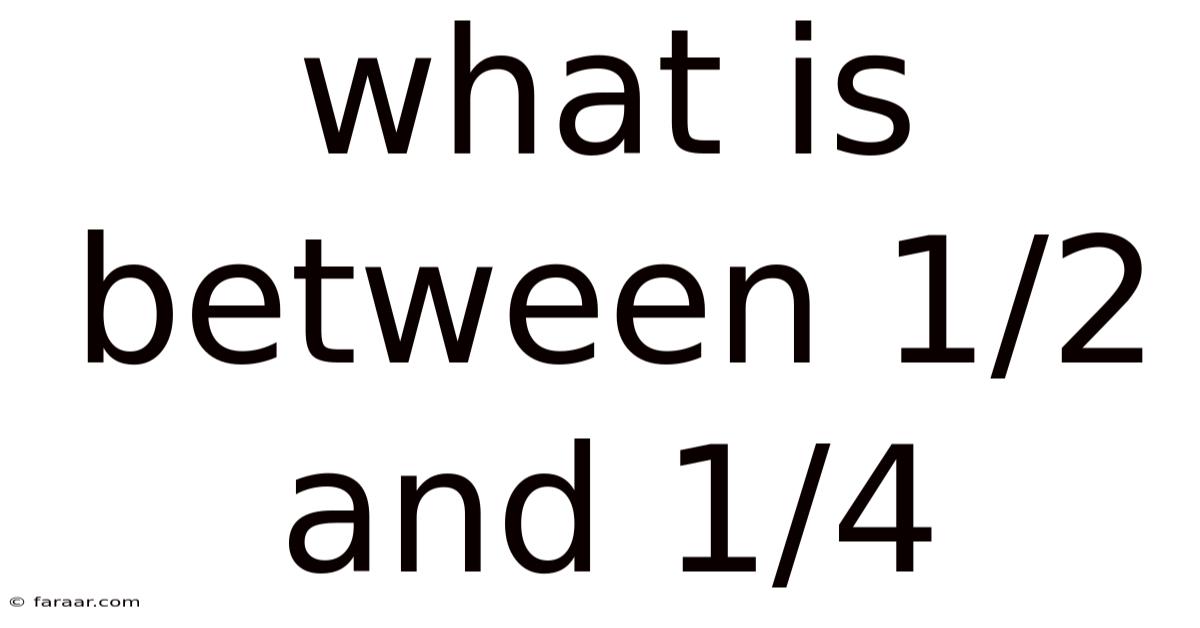
Table of Contents
Decoding the Numbers Between 1/2 and 1/4: A Deep Dive into Fractions and Number Lines
What lies between 1/2 and 1/4? This seemingly simple question opens the door to a fascinating exploration of fractions, rational numbers, and the infinite nature of numbers. Understanding the space between these two fractions requires a grasp of fundamental mathematical concepts and an appreciation for the elegance of mathematical systems. This article will not only answer the initial question but delve deeper into the underlying principles, equipping you with a solid understanding of fractional arithmetic and number representation.
Understanding Fractions: A Foundational Review
Before we tackle the numbers between 1/2 and 1/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 1/2, the denominator 2 tells us the whole is divided into two equal parts, and the numerator 1 indicates we are considering one of those parts. Similarly, 1/4 represents one part out of four equal parts.
Visualizing Fractions on a Number Line
A number line provides a powerful visual tool for understanding the relationship between fractions. Imagine a number line stretching from 0 to 1. The point 0 represents nothing, and the point 1 represents the whole. The midpoint of this line is 1/2, perfectly bisecting the space between 0 and 1. If we divide the space between 0 and 1/2 into two equal parts, we find 1/4 at the first division mark.
Now, the question becomes clear: what lies between the marks representing 1/4 and 1/2 on our number line? The immediate answer is that there are infinitely many numbers!
Finding Fractions Between 1/2 and 1/4: A Systematic Approach
To systematically find fractions between 1/2 and 1/4, we can employ a few different methods. These methods help us understand not only the existence of these fractions but also how to generate them.
Method 1: Finding a Common Denominator
The simplest approach involves finding a common denominator for 1/2 and 1/4. Since 4 is a multiple of 2, we can easily rewrite 1/2 with a denominator of 4:
1/2 = 2/4
Now, we can clearly see that the fraction 3/4 is greater than 1/2. To determine the value between 1/4 and 1/2, let's consider values with a denominator larger than 4. A simple approach is to double the denominator:
1/2 = 4/8 1/4 = 2/8
Now we can see that 3/8 lies precisely between 1/4 and 1/2.
We can continue this process by using progressively larger common denominators. For instance, if we use a denominator of 16:
1/2 = 8/16 1/4 = 4/16
This reveals several fractions between 1/4 and 1/2, including 5/16, 6/16 (which simplifies to 3/8), and 7/16.
Method 2: Averaging the Fractions
Another effective method involves averaging the two fractions. To find the midpoint between 1/2 and 1/4, we add them together and divide by 2:
(1/2 + 1/4) / 2 = (2/4 + 1/4) / 2 = 3/4 / 2 = 3/8
This confirms our earlier finding that 3/8 lies precisely halfway between 1/4 and 1/2. We can repeat this process with 1/4 and 3/8, or 3/8 and 1/2, to find more fractions.
Method 3: Using Decimal Representations
Converting the fractions to decimals can also provide a visual understanding:
1/2 = 0.5 1/4 = 0.25
Now, it's easier to identify decimals between 0.25 and 0.5, such as 0.3, 0.375, 0.4, and so on. These decimals can then be converted back into fractions. For instance:
0.3 = 3/10 0.375 = 3/8 0.4 = 2/5
This method emphasizes that there are countless numbers between 0.25 and 0.5, all representable as fractions.
The Infinitude of Rational Numbers Between 1/2 and 1/4
The key takeaway is that there are infinitely many rational numbers (fractions) between 1/2 and 1/4. No matter how many fractions we find, we can always find more by using larger denominators or repeatedly averaging existing fractions. This illustrates the density of rational numbers on the number line: between any two distinct rational numbers, there always exists another rational number.
Extending the Concept: Irrational Numbers
While we've focused on rational numbers, it's important to remember that there are also irrational numbers between 1/2 and 1/4. Irrational numbers are numbers that cannot be expressed as a ratio of two integers. Examples include π (pi) and √2 (the square root of 2). While we cannot express these precisely as fractions, they exist on the number line and fall within the interval between 1/4 and 1/2.
Real Numbers and the Continuum
The set of all rational and irrational numbers together constitutes the real numbers. The real numbers form a continuum, meaning there are no gaps in the number line. Every point on the number line corresponds to a real number, and between any two distinct real numbers, there are infinitely many other real numbers.
Practical Applications and Real-World Examples
Understanding the concept of fractions and their density is crucial in various real-world scenarios:
- Measurement: Imagine measuring ingredients for a recipe. You might need 3/8 of a cup of sugar, a fraction lying precisely between 1/4 and 1/2 cups.
- Data Analysis: In statistics, fractions are frequently used to represent proportions and probabilities. Understanding the relationships between fractions allows for more precise analysis.
- Engineering and Design: In fields like architecture and engineering, precise measurements and proportions are essential. Fractions help in achieving that level of precision.
Frequently Asked Questions (FAQs)
Q: Is there a largest fraction between 1/4 and 1/2?
A: No. As we've seen, we can always find a larger fraction by increasing the denominator.
Q: Can all numbers between 1/4 and 1/2 be expressed as fractions?
A: No. While many can, irrational numbers exist within this range and cannot be expressed as fractions.
Q: How can I easily find more fractions between 1/4 and 1/2?
A: Use the methods described above: finding a common denominator, averaging fractions, or converting to decimals and back to fractions. The key is to continuously increase the denominator.
Q: What is the significance of the infinite number of fractions between 1/4 and 1/2?
A: This illustrates the density of rational numbers on the number line and hints at the richness and complexity of the real number system.
Conclusion
The seemingly simple question of "What is between 1/2 and 1/4?" leads us down a fascinating path of mathematical exploration. We've learned that there are infinitely many rational numbers and even irrational numbers within this range. Understanding fractions, rational numbers, and their density on the number line is crucial not only for mathematical proficiency but also for navigating various aspects of the real world. This exploration highlights the depth and elegance inherent in even seemingly simple mathematical concepts. The journey from a simple question about fractions to a deeper understanding of the real number system demonstrates the power of mathematical inquiry and the interconnectedness of mathematical ideas. This exploration showcases how a single question can unlock a wealth of knowledge and enhance our appreciation for the beauty and complexity of mathematics.
Latest Posts
Latest Posts
-
A Negative Divided By A Positive
Sep 08, 2025
-
6 Is 3 Of What Number
Sep 08, 2025
-
Has Membrane Bound Organelles Prokaryotic Or Eukaryotic
Sep 08, 2025
-
What Is 1 12 In A Decimal
Sep 08, 2025
-
Complete This Table Relating The Values Of Ecell
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Is Between 1/2 And 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.