Graph Of X 2 Y 2 9
faraar
Sep 16, 2025 · 6 min read
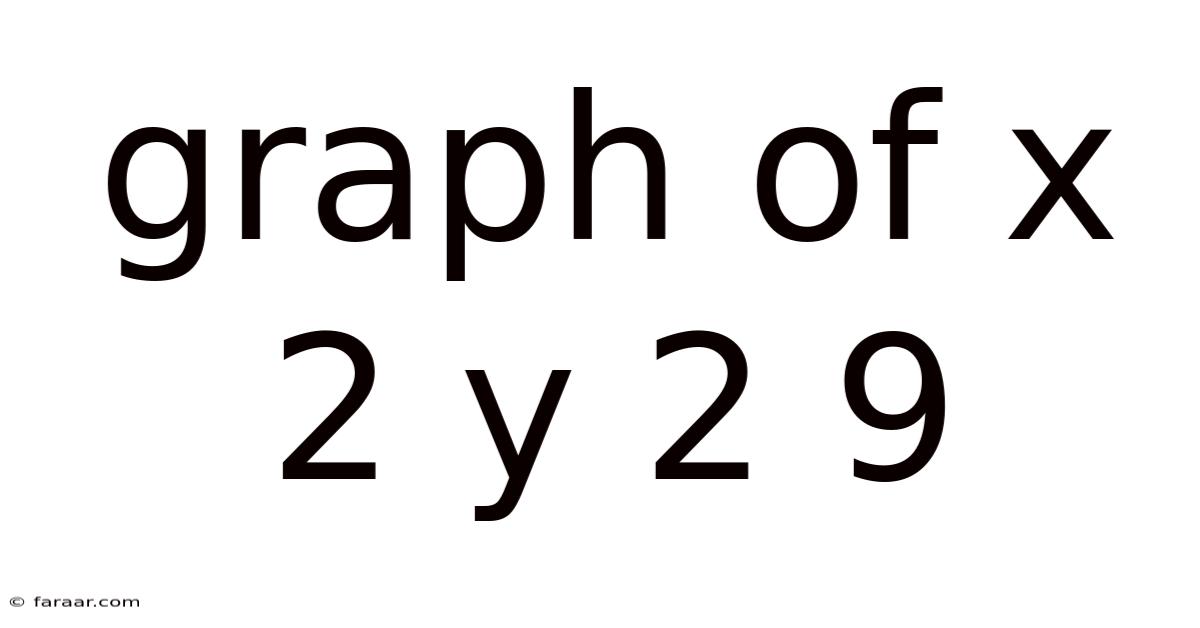
Table of Contents
Unveiling the Secrets of x² + y² = 9: A Comprehensive Exploration of a Circle's Equation
The equation x² + y² = 9 might seem simple at first glance, but it holds the key to understanding a fundamental geometric shape: the circle. This article will delve deep into this equation, exploring its graphical representation, its derivation from the distance formula, and its applications in various fields. We'll also tackle common misconceptions and answer frequently asked questions. By the end, you'll have a comprehensive grasp of this seemingly simple, yet powerful, mathematical concept.
Understanding the Equation: x² + y² = 9
At its core, x² + y² = 9 represents the equation of a circle. Let's break down what each part means:
- x² and y²: These terms represent the squares of the x and y coordinates of any point on the circle.
- = 9: This indicates that the sum of the squares of the x and y coordinates is always equal to 9 for every point lying on the circle.
This equation is a specific case of the general equation of a circle: (x - h)² + (y - k)² = r², where (h, k) represents the center of the circle and r represents its radius. In our case, x² + y² = 9, we can see that h = 0, k = 0, and r² = 9. Therefore, the equation represents a circle centered at the origin (0, 0) with a radius of √9 = 3.
Graphical Representation: Visualizing the Circle
The graphical representation of x² + y² = 9 is simply a circle with a radius of 3 units, centered at the origin (0, 0) on the Cartesian coordinate plane. This means that every point (x, y) that satisfies the equation is located exactly 3 units away from the origin.
To visualize this:
- Locate the center: The center of the circle is at (0, 0).
- Determine the radius: The radius is 3 units.
- Plot points: Start by plotting points 3 units away from the origin along the x and y axes: (3, 0), (-3, 0), (0, 3), and (0, -3). You can also plot additional points to get a clearer picture of the circle.
- Draw the circle: Connect the plotted points to form a smooth circle.
You can use graphing software or even graph paper to accurately plot this circle. The beauty of this equation lies in its simplicity – a concise mathematical representation of a visually elegant shape.
Deriving the Equation from the Distance Formula
The equation x² + y² = 9 can be derived directly from the distance formula. The distance formula, which calculates the distance between two points (x₁, y₁) and (x₂, y₂), is given by:
d = √[(x₂ - x₁)² + (y₂ - y₁)²]
In the case of our circle, we are interested in the distance between any point (x, y) on the circle and the origin (0, 0). We know that this distance is always equal to the radius, which is 3. Substituting these values into the distance formula, we get:
3 = √[(x - 0)² + (y - 0)²]
Squaring both sides to eliminate the square root, we obtain:
9 = (x - 0)² + (y - 0)²
Simplifying, we arrive at the familiar equation:
x² + y² = 9
Applications of the Circle Equation in Various Fields
The seemingly simple equation x² + y² = 9 has far-reaching applications across various fields:
-
Physics: Circular motion is a fundamental concept in physics, and this equation helps describe the path of objects moving in a circle with a constant radius. Think of a satellite orbiting the Earth – its path can be modeled using a similar equation.
-
Engineering: Circles are used extensively in engineering designs, from gears and wheels to pipelines and structural components. Understanding the equation of a circle is crucial for accurate calculations and precise designs.
-
Computer Graphics: In computer graphics, the equation is used to generate and manipulate circular shapes on screens. This forms the basis of many visual elements in games, animations, and user interfaces.
-
Mathematics: This equation serves as a foundation for more advanced mathematical concepts, such as conic sections (ellipses, parabolas, and hyperbolas). Understanding circles is essential for grasping these more complex shapes.
-
Mapping and Geography: Circular regions are often used in geographical mapping to represent areas of influence, zones of coverage or proximity analyses. The equation helps define these regions accurately.
Common Misconceptions and Clarifications
Here are some common misconceptions surrounding the equation x² + y² = 9:
-
Misconception 1: The equation only represents points on the circle's circumference. Clarification: While the equation defines the circle's perimeter, it also implicitly defines the interior region. Any point (x, y) where x² + y² < 9 lies inside the circle, while points where x² + y² > 9 lie outside it.
-
Misconception 2: The equation only works for circles centered at the origin. Clarification: This is a specific case. The general equation of a circle, (x - h)² + (y - k)² = r², accommodates circles centered at any point (h, k).
-
Misconception 3: Understanding the equation is only for mathematicians. Clarification: The concept is used across various disciplines and understanding its implications can enhance problem-solving skills and applications in real world scenarios.
Frequently Asked Questions (FAQ)
Q1: What if the equation was x² + y² = r², where r is any positive number?
A1: This represents a circle centered at the origin (0, 0) with a radius of 'r'. The value of r determines the size of the circle.
Q2: How can I find the area of the circle represented by x² + y² = 9?
A2: The area of a circle is given by the formula A = πr². Since r = 3, the area is A = π(3)² = 9π square units.
Q3: How can I find the circumference of the circle represented by x² + y² = 9?
A3: The circumference of a circle is given by the formula C = 2πr. With r = 3, the circumference is C = 2π(3) = 6π units.
Q4: Can this equation be used to represent a circle in three dimensions?
A4: No, this equation only represents a circle in two dimensions (the xy-plane). In three dimensions, it would represent a cylinder. The equation of a sphere, however, is an extension to three dimensions: (x - a)² + (y - b)² + (z - c)² = r², where (a, b, c) is the center and r is the radius.
Q5: What happens if the equation is x² + y² = -9?
A5: There are no real solutions to this equation. The sum of two squares cannot be negative, therefore, this equation doesn't represent any geometrical shape in the real number system.
Conclusion: The Enduring Significance of x² + y² = 9
The equation x² + y² = 9, while seemingly simple, holds immense mathematical significance and practical applications. Understanding its derivation, graphical representation, and applications across various fields is crucial for anyone interested in mathematics, physics, engineering, or computer science. This exploration has hopefully illuminated the rich depth hidden within this fundamental equation, showcasing its power and enduring relevance in the world around us. Remember that even seemingly simple concepts can unlock profound understanding when examined in detail. Keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
What Is 1 4 Of 3 4 As A Fraction
Sep 16, 2025
-
How To Find A Leg On A Right Triangle
Sep 16, 2025
-
2x 2 7x 9 0 Quadratic Formula
Sep 16, 2025
-
Find The Average Value Of A Function
Sep 16, 2025
-
4 9 Rounded To The Nearest Tenth
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Graph Of X 2 Y 2 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.