Graph Of X 2 2x 2
faraar
Sep 23, 2025 · 6 min read
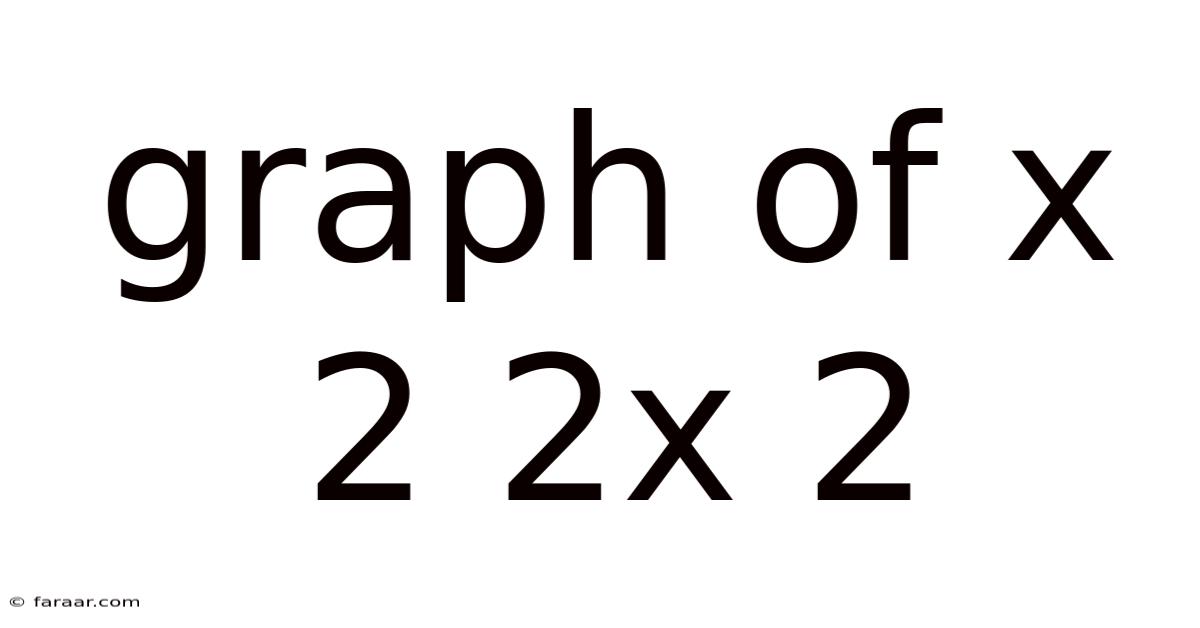
Table of Contents
Exploring the Graph of x² + 2x - 2: A Comprehensive Guide
Understanding the graph of a quadratic function like x² + 2x - 2 is fundamental to grasping core concepts in algebra and calculus. This comprehensive guide will delve into the various aspects of this specific quadratic, exploring its properties, how to graph it accurately, and the underlying mathematical principles involved. We'll cover everything from finding the vertex and intercepts to discussing its behavior and applications. By the end, you'll not only be able to graph this function but also understand the methods used to analyze any quadratic equation.
I. Understanding Quadratic Functions
Before we dive into the specifics of x² + 2x - 2, let's establish a foundational understanding of quadratic functions. A quadratic function is a polynomial function of degree two, meaning the highest power of the variable (x, in this case) is 2. The general form of a quadratic function is:
f(x) = ax² + bx + c
where a, b, and c are constants, and a ≠ 0 (otherwise, it wouldn't be a quadratic). The graph of a quadratic function is always a parabola—a symmetrical U-shaped curve. The value of a determines whether the parabola opens upwards (a > 0) or downwards (a < 0).
In our specific case, x² + 2x - 2, we have a = 1, b = 2, and c = -2. Since a = 1 > 0, the parabola opens upwards.
II. Finding Key Features of the Graph
To accurately graph x² + 2x - 2, we need to identify several key features:
- Vertex: The vertex is the lowest (or highest, if the parabola opens downwards) point on the parabola. The x-coordinate of the vertex is given by:
x = -b / 2a
In our case, x = -2 / (2 * 1) = -1. To find the y-coordinate, substitute this x-value back into the function:
f(-1) = (-1)² + 2(-1) - 2 = -3
Therefore, the vertex is (-1, -3).
- x-intercepts (Roots): The x-intercepts are the points where the graph intersects the x-axis (where y = 0). To find them, we solve the quadratic equation:
x² + 2x - 2 = 0
This quadratic equation doesn't factor easily, so we'll use the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values, we get:
x = [-2 ± √(2² - 4 * 1 * -2)] / 2 * 1 = [-2 ± √12] / 2 = -1 ± √3
Therefore, the x-intercepts are approximately (-2.732, 0) and (0.732, 0).
- y-intercept: The y-intercept is the point where the graph intersects the y-axis (where x = 0). This is simply the value of c:
f(0) = -2
So the y-intercept is (0, -2).
III. Completing the Square and Vertex Form
Another useful approach to understanding the parabola is to rewrite the quadratic equation in vertex form:
f(x) = a(x - h)² + k
where (h, k) is the vertex. This is achieved by completing the square:
x² + 2x - 2 = (x² + 2x + 1) - 1 - 2 = (x + 1)² - 3
This confirms our previously calculated vertex of (-1, -3). The vertex form clearly shows the parabola's vertex and how it shifts from the basic parabola y = x².
IV. Axis of Symmetry
The axis of symmetry is a vertical line that divides the parabola into two mirror-image halves. Its equation is given by:
x = h
where (h, k) is the vertex. In our case, the axis of symmetry is x = -1.
V. Graphing the Parabola
Now that we have all the key features, we can accurately graph the parabola:
- Plot the vertex: (-1, -3)
- Plot the intercepts: (0, -2), approximately (-2.732, 0), and (0.732, 0).
- Draw the axis of symmetry: x = -1.
- Sketch the parabola: Remember it opens upwards since a = 1 > 0. Use the symmetry to guide your drawing. The parabola should be symmetrical around the axis of symmetry (x = -1). You can plot additional points if needed for greater accuracy.
VI. Analyzing the Graph
The graph provides valuable information about the function's behavior:
- Domain: The domain of a quadratic function is all real numbers, (-∞, ∞).
- Range: Since the parabola opens upwards and the vertex is at (-1, -3), the range is [-3, ∞).
- Increasing/Decreasing: The function is decreasing for x < -1 and increasing for x > -1.
- Minimum Value: The minimum value of the function is -3, which occurs at the vertex.
VII. Applications of Quadratic Functions
Quadratic functions have numerous real-world applications, including:
- Projectile Motion: The trajectory of a projectile (like a ball thrown in the air) follows a parabolic path.
- Area Optimization: Finding the maximum area of a rectangle given a fixed perimeter involves solving a quadratic equation.
- Engineering and Physics: Many physical phenomena can be modeled using quadratic equations, such as the relationship between distance and time for accelerating objects.
VIII. Further Exploration: Transformations of the Parabola
Understanding the basic parabola y = x² allows us to easily visualize transformations. Our function, x² + 2x - 2, can be seen as a transformation of the basic parabola:
- Horizontal Shift: The (x + 1)² term indicates a horizontal shift of 1 unit to the left.
- Vertical Shift: The -3 term indicates a vertical shift of 3 units down.
These transformations help us understand how the graph relates to the simpler parent function y = x².
IX. Frequently Asked Questions (FAQ)
-
Q: What is the discriminant of the quadratic equation?
A: The discriminant is the part under the square root in the quadratic formula (b² - 4ac). In our case, it's 2² - 4(1)(-2) = 12. A positive discriminant indicates two distinct real roots (x-intercepts), which we confirmed earlier.
-
Q: How can I find additional points to improve the accuracy of my graph?
A: You can choose any x-values and substitute them into the function to find the corresponding y-values. For example, if you choose x = 1, f(1) = 1² + 2(1) - 2 = 1. So, the point (1, 1) is on the graph.
-
Q: What if 'a' was negative?
A: If a were negative, the parabola would open downwards, and the vertex would represent a maximum value instead of a minimum value. The other features (intercepts, axis of symmetry) would still be calculated using the same methods.
-
Q: Are there other methods to solve quadratic equations besides the quadratic formula?
A: Yes, other methods include factoring, completing the square, and graphical methods. The best method depends on the specific quadratic equation.
X. Conclusion
The graph of x² + 2x - 2, a parabola opening upwards, is fully defined by its vertex (-1, -3), x-intercepts (-1 ± √3), y-intercept (0, -2), and axis of symmetry (x = -1). Understanding how to find these key features, along with the broader principles of quadratic functions and their applications, is essential for success in algebra and related fields. By mastering these techniques, you can confidently analyze and graph any quadratic function you encounter. Remember that practice is key—the more you work with quadratic equations, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
What Holds An Ionic Bond Together
Sep 23, 2025
-
Which Element Has The Following Ground State Electron Configuration
Sep 23, 2025
-
Boiling Point Of Benzene In Celsius
Sep 23, 2025
-
Is The Surface Area The Same As Area
Sep 23, 2025
-
Sin X Tan X Cos X
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Graph Of X 2 2x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.