Sin X Tan X + Cos X
faraar
Sep 23, 2025 · 5 min read
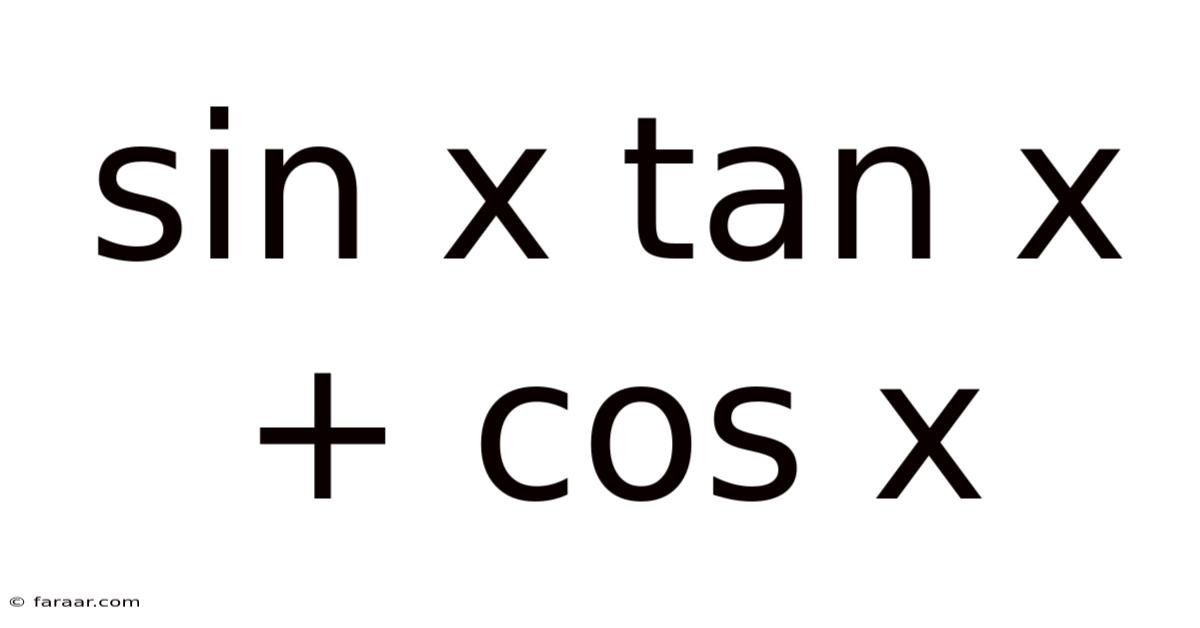
Table of Contents
Exploring the Trigonometric Expression: sin x tan x + cos x
Understanding trigonometric identities and expressions is fundamental to mastering trigonometry. This article delves deep into the expression sin x tan x + cos x, exploring its simplification, graphical representation, and practical applications. We will unravel its intricacies, providing a comprehensive understanding suitable for students and anyone interested in deepening their knowledge of trigonometry. This exploration will cover simplification techniques, examining its behavior across different quadrants, and addressing frequently asked questions.
Understanding the Components: sin x, tan x, and cos x
Before embarking on the analysis of the entire expression, let's refresh our understanding of its individual components: sin x, tan x, and cos x. These are fundamental trigonometric functions defined in relation to a right-angled triangle.
- sin x (sine of x): The ratio of the length of the side opposite the angle x to the length of the hypotenuse.
- tan x (tangent of x): The ratio of the length of the side opposite the angle x to the length of the side adjacent to the angle x. It can also be expressed as sin x / cos x.
- cos x (cosine of x): The ratio of the length of the side adjacent to the angle x to the length of the hypotenuse.
These functions are cyclical, repeating their values over intervals of 2π (or 360 degrees). Understanding their individual properties is crucial for analyzing their combined behavior in the given expression.
Simplifying sin x tan x + cos x
The expression sin x tan x + cos x can be simplified using trigonometric identities. Recall that tan x = sin x / cos x. Substituting this into our expression, we get:
sin x (sin x / cos x) + cos x
This simplifies to:
(sin²x) / cos x + cos x
To further simplify, we find a common denominator:
(sin²x + cos²x) / cos x
Now, we use the fundamental Pythagorean identity: sin²x + cos²x = 1. Substituting this, we obtain:
1 / cos x
Finally, we recognize that 1 / cos x is equal to sec x (secant of x). Therefore, the simplified expression is:
sec x
Graphical Representation and Analysis
Visualizing the expression is key to grasping its behavior. The graph of y = sec x exhibits asymptotes where cos x = 0 (i.e., at x = π/2 + nπ, where n is an integer). This is because the function is undefined when the denominator is zero. The graph displays a periodic pattern, repeating every 2π radians (or 360 degrees), reflecting the cyclical nature of trigonometric functions. The graph's peaks and valleys represent the maximum and minimum values of the secant function, highlighting its unbounded nature. Observing the graph helps illustrate the relationship between the original complex expression and its simplified form, demonstrating their equivalence.
Behavior Across Different Quadrants
The behavior of sec x varies across the four quadrants of the unit circle:
- Quadrant I (0° to 90°): Both sin x and cos x are positive, resulting in a positive sec x.
- Quadrant II (90° to 180°): cos x is negative, so sec x is negative.
- Quadrant III (180° to 270°): cos x is negative, so sec x is negative.
- Quadrant IV (270° to 360°): cos x is positive, so sec x is positive.
Understanding this quadrantal behavior provides a complete picture of the function's range and how it responds to changes in the input angle x.
Practical Applications
The expression, and its simplified form sec x, has various applications in different fields:
- Physics: In wave phenomena, the secant function can model certain oscillatory behaviors. It appears in equations related to wave propagation and other periodic processes.
- Engineering: Secant and other trigonometric functions are essential tools for solving problems involving angles, forces, and displacements in structural analysis and mechanics. For instance, calculating stresses in inclined beams or analyzing forces in inclined planes frequently involves trigonometric functions.
- Navigation: Trigonometry, including the secant function, plays a crucial role in navigation, particularly in determining distances and bearings. It’s integral to GPS systems and other navigational technologies.
- Computer Graphics: Trigonometric functions are fundamental in computer graphics for transformations, rotations, and projections, which ultimately contribute to the rendering of 3D images.
Frequently Asked Questions (FAQ)
Q1: Can the expression be simplified in other ways?
A1: While the simplification to sec x is the most concise and generally preferred method, other equivalent expressions could be derived using different trigonometric identities. However, sec x offers the most compact and readily interpretable representation.
Q2: What are the domain and range of the expression?
A2: The domain of sec x (and thus the original expression) is all real numbers except for values of x where cos x = 0 (x = π/2 + nπ, where n is an integer). The range of sec x is (-∞, -1] ∪ [1, ∞).
Q3: How does the expression behave as x approaches the asymptotes?
A3: As x approaches values where cos x = 0, the value of sec x approaches positive or negative infinity, depending on the direction of approach. This is reflected in the vertical asymptotes seen in the graph of sec x.
Q4: Are there any special cases where the expression simplifies further?
A4: While sec x is the most simplified general form, specific values of x might lead to simpler numerical results. For instance, if x = 0, sec x = 1. However, the general simplified form remains sec x.
Q5: Can this expression be used to solve trigonometric equations?
A5: Yes, the simplified form sec x can be helpful in solving trigonometric equations. By substituting sec x, we can potentially simplify the equation and make it easier to solve for x.
Conclusion
The trigonometric expression sin x tan x + cos x, ultimately simplified to sec x, offers a rich exploration into the world of trigonometric identities and their applications. By understanding its simplification, graphical representation, quadrantal behavior, and diverse applications, we gain a profound appreciation for its significance in mathematics and various scientific and engineering fields. This comprehensive analysis provides a solid foundation for further exploration of more complex trigonometric expressions and their practical implications. Remember that consistent practice and a deep understanding of fundamental trigonometric identities are key to mastering such expressions.
Latest Posts
Latest Posts
-
Do You Multiply Or Add Exponents In Parentheses
Sep 23, 2025
-
Five To The Power Of Three
Sep 23, 2025
-
Can You Close A Dead Persons Eyes
Sep 23, 2025
-
Tricky Math Problems For 8th Graders
Sep 23, 2025
-
Difference Between Hydrochloric Acid And Muriatic Acid
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Sin X Tan X + Cos X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.