Given That Abc Def Solve For X And Y
faraar
Aug 28, 2025 · 7 min read
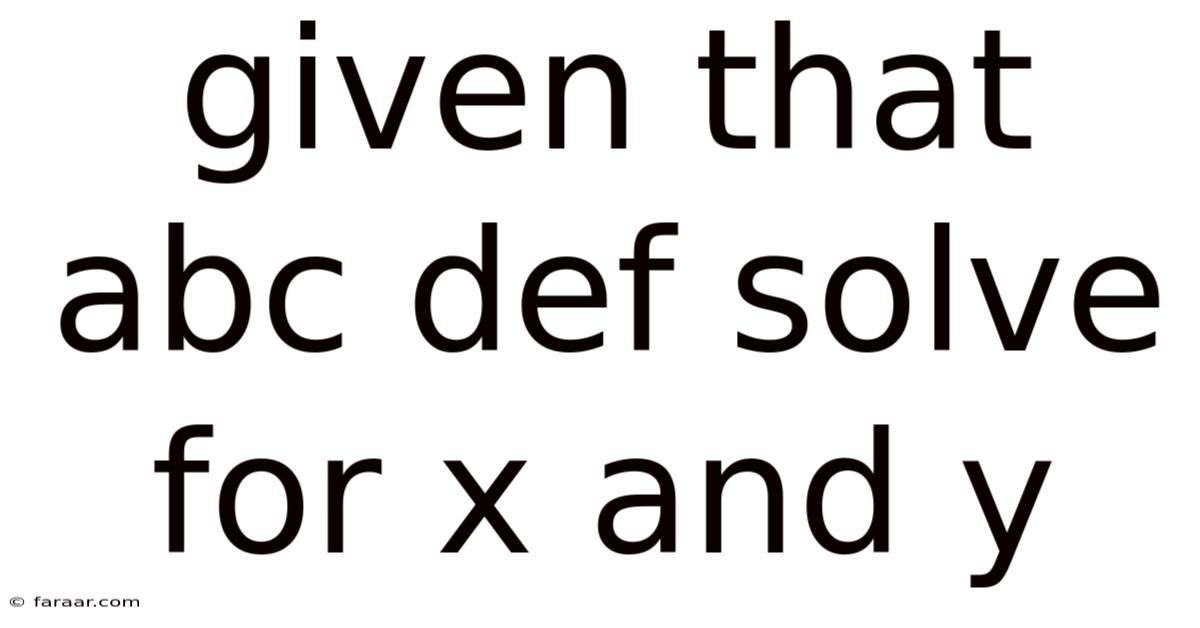
Table of Contents
Solving for X and Y: A Comprehensive Guide to Simultaneous Equations
This article provides a comprehensive guide on how to solve for x and y in simultaneous equations, a fundamental concept in algebra. We'll explore various methods, delve into the underlying mathematical principles, and offer practical examples to solidify your understanding. Understanding simultaneous equations is crucial for various fields, from physics and engineering to economics and computer science. This guide is designed for students of all levels, from beginners grappling with the basics to those seeking a deeper understanding of the subject. We'll tackle the problem systematically, ensuring you can confidently solve for x and y given any pair of linear equations.
Introduction to Simultaneous Equations
Simultaneous equations, also known as systems of equations, involve two or more equations with two or more variables. The goal is to find the values of the variables that satisfy all the equations simultaneously. In the context of "given abc def solve for x and y," we assume 'abc' and 'def' represent two equations containing variables x and y. These equations could be linear (straight lines when graphed), quadratic (parabolas), or even more complex forms. This guide focuses primarily on solving systems of linear equations, which are the most common type encountered in introductory algebra.
Types of Simultaneous Equations
Before we delve into solving methods, let's clarify the types of simultaneous equations we'll be dealing with:
-
Linear Simultaneous Equations: These are equations where the highest power of each variable is 1. They represent straight lines when graphed. Examples include:
- 2x + 3y = 7
- x - y = 1
-
Non-linear Simultaneous Equations: These equations involve variables raised to powers greater than 1, such as quadratic, cubic, or other higher-order equations. These are more complex to solve and often require advanced techniques. We will not cover these in detail in this introductory guide.
Methods for Solving Linear Simultaneous Equations
There are several methods for solving linear simultaneous equations. The most common are:
-
Elimination Method: This method involves manipulating the equations to eliminate one variable, allowing you to solve for the other.
-
Substitution Method: This method involves solving one equation for one variable and substituting the expression into the other equation.
-
Graphical Method: This method involves graphing both equations and finding the point of intersection, which represents the solution.
Let's explore each method in detail, using examples to illustrate the process.
1. The Elimination Method
The elimination method aims to eliminate one variable by adding or subtracting the equations. This requires manipulating the equations so that the coefficients of one variable are opposites. Here's a step-by-step guide:
Steps:
- Choose a variable to eliminate: Decide which variable is easier to eliminate based on the coefficients.
- Multiply equations (if necessary): Multiply one or both equations by a constant to make the coefficients of the chosen variable opposites.
- Add or subtract the equations: Add the equations if the coefficients are opposites; subtract if they are the same. This will eliminate the chosen variable.
- Solve for the remaining variable: Solve the resulting equation for the remaining variable.
- Substitute back: Substitute the value you found back into either of the original equations to solve for the other variable.
- Check your solution: Substitute both values back into both original equations to verify that they satisfy both equations.
Example:
Solve the following system of equations using the elimination method:
- 2x + y = 7
- x - y = 2
Solution:
-
Notice that the coefficients of 'y' are opposites (+1 and -1). We can eliminate 'y' by adding the two equations.
-
Adding the equations: (2x + y) + (x - y) = 7 + 2 which simplifies to 3x = 9.
-
Solving for x: x = 9/3 = 3
-
Substituting x = 3 into the first equation (2x + y = 7): 2(3) + y = 7, which simplifies to 6 + y = 7.
-
Solving for y: y = 7 - 6 = 1
-
Therefore, the solution is x = 3 and y = 1. Let's check:
- 2(3) + 1 = 7 (Correct)
- 3 - 1 = 2 (Correct)
2. The Substitution Method
The substitution method involves solving one equation for one variable and then substituting that expression into the other equation. This will reduce the system to a single equation with one variable.
Steps:
- Solve for one variable: Solve one of the equations for one variable in terms of the other variable.
- Substitute: Substitute the expression from step 1 into the other equation.
- Solve for the remaining variable: Solve the resulting equation for the remaining variable.
- Substitute back: Substitute the value you found back into either of the original equations or the expression from step 1 to solve for the other variable.
- Check your solution: Substitute both values back into both original equations to verify the solution.
Example:
Solve the same system of equations using the substitution method:
- 2x + y = 7
- x - y = 2
Solution:
-
Solve the second equation for x: x = y + 2
-
Substitute this expression for x into the first equation: 2(y + 2) + y = 7
-
Simplify and solve for y: 2y + 4 + y = 7 => 3y = 3 => y = 1
-
Substitute y = 1 back into x = y + 2: x = 1 + 2 = 3
-
The solution is x = 3 and y = 1 (same as the elimination method). Check the solution as before.
3. The Graphical Method
The graphical method involves plotting both equations on a graph. The point where the two lines intersect represents the solution (x, y).
Steps:
- Rewrite equations in slope-intercept form: Rewrite each equation in the form y = mx + b, where m is the slope and b is the y-intercept.
- Plot the lines: Plot each line on a graph using the slope and y-intercept.
- Find the intersection point: Identify the point where the two lines intersect. The x and y coordinates of this point represent the solution.
Example:
Let's use the same system of equations:
- 2x + y = 7 => y = -2x + 7
- x - y = 2 => y = x - 2
Plot these two lines. You'll find they intersect at the point (3, 1), confirming our solution from the previous methods.
Handling Special Cases
Sometimes, systems of equations may result in special cases:
-
No Solution: The lines are parallel and never intersect. This occurs when the equations have the same slope but different y-intercepts. Example: x + y = 1 and x + y = 3.
-
Infinite Solutions: The lines are coincident (they are the same line). This occurs when the equations are multiples of each other. Example: x + y = 1 and 2x + 2y = 2.
Explanation of the Underlying Mathematical Principles
The methods described above are based on the fundamental principles of linear algebra. The elimination method relies on the properties of equality, allowing us to add or subtract equations without changing the solution. The substitution method uses the transitive property of equality, allowing us to replace one expression with an equivalent one. The graphical method visually represents the solution as the point where the constraints defined by each equation are simultaneously satisfied.
Frequently Asked Questions (FAQ)
Q: Which method is the best?
A: There's no single "best" method. The choice depends on the specific equations. The elimination method is often efficient when coefficients are easily manipulated. The substitution method works well when one variable is easily isolated. The graphical method is useful for visualizing the solution but can be less precise than algebraic methods.
Q: What if the equations are non-linear?
A: Solving non-linear simultaneous equations is more complex and requires advanced techniques beyond the scope of this introductory guide. These often involve substitution, factorization, or numerical methods.
Q: What if I get a solution that doesn't check out?
A: Carefully review your steps. A common error is making mistakes in algebraic manipulations or substitutions.
Conclusion
Solving simultaneous equations is a fundamental skill in algebra with broad applications. This guide has provided a comprehensive overview of the most common methods – elimination, substitution, and graphical – highlighting their steps, principles, and practical applications. By mastering these techniques, you'll be well-equipped to tackle a wide range of mathematical problems and deepen your understanding of algebraic concepts. Remember to practice regularly to build confidence and proficiency in solving these types of equations. With practice, you'll find solving for x and y becomes second nature.
Latest Posts
Latest Posts
-
How To Find The Average Of Test Scores
Aug 28, 2025
-
Atomic Mass Equals The Number Of
Aug 28, 2025
-
The Sum Of A Number And 9
Aug 28, 2025
-
How Did Lenore Die In The Raven
Aug 28, 2025
-
Find The Missing Term In The Geometric Sequence
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about Given That Abc Def Solve For X And Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.