Find Two Consecutive Even Numbers Whose Sum Is 126
faraar
Aug 29, 2025 · 7 min read
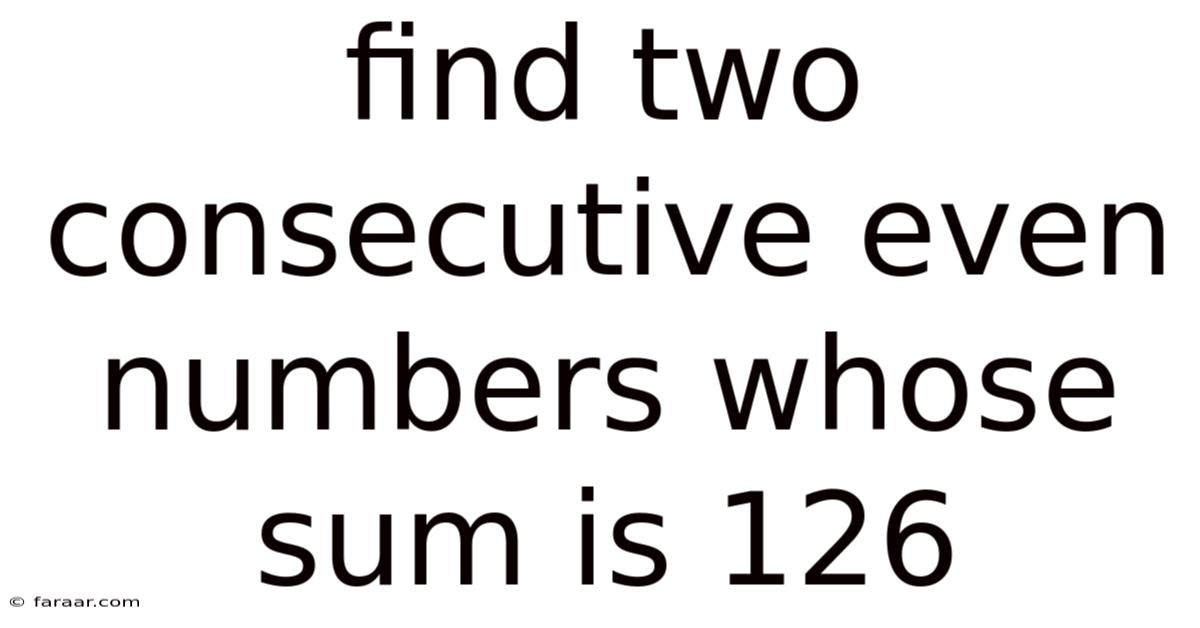
Table of Contents
Finding Consecutive Even Numbers: A Deep Dive into Problem Solving
Finding two consecutive even numbers whose sum is 126 might seem like a simple math problem, perfect for elementary school. However, this seemingly basic question offers a fantastic opportunity to explore several mathematical concepts, from basic algebra to more advanced problem-solving strategies. This article will not only solve the problem but also delve into the underlying principles, offering a comprehensive understanding suitable for students of various levels. We'll explore different approaches, discuss the importance of mathematical reasoning, and even touch upon the application of these techniques in more complex scenarios.
Understanding the Problem: Defining Consecutive Even Numbers
Before we jump into solving the problem, let's clarify the terminology. Consecutive even numbers are numbers that follow each other in sequence, with a difference of 2 between them. For example, 2 and 4, 10 and 12, or 100 and 102 are all pairs of consecutive even numbers. Our task is to find two such numbers that add up to 126.
Method 1: The Algebraic Approach
This is the most common and arguably the most elegant method for solving this type of problem. We can represent the two consecutive even numbers algebraically.
Let's say the first even number is x. Since the numbers are consecutive even numbers, the next even number will be x + 2. The problem states that their sum is 126. Therefore, we can write the equation:
x + (x + 2) = 126
Now, we can solve for x:
- Combine like terms: 2x + 2 = 126
- Subtract 2 from both sides: 2x = 124
- Divide both sides by 2: x = 62
So, the first even number is 62. The next consecutive even number is x + 2 = 62 + 2 = 64.
Therefore, the two consecutive even numbers are 62 and 64. We can check our answer: 62 + 64 = 126. This confirms our solution.
Method 2: The Intuitive Approach (Guess and Check)
While the algebraic method is precise and efficient, particularly for more complex problems, this problem lends itself to an intuitive approach. We can start by estimating. Since we are looking for two numbers that add up to 126, a reasonable guess might be around 60. If we choose 60, the next consecutive even number is 62. Their sum is 122 (60 + 62 = 122), which is slightly less than 126. Let’s try increasing both numbers by 2: 62 and 64. Their sum is 126. Voila! We've found our answer.
This method is suitable for smaller numbers and simpler problems. However, it becomes less efficient and more prone to errors as the numbers increase.
Method 3: Using Arithmetic Mean
Another approach utilizes the concept of the arithmetic mean (average). The arithmetic mean of two numbers is their sum divided by 2. In our problem, the sum of the two consecutive even numbers is 126. Therefore, their mean is 126 / 2 = 63.
Since the two numbers are consecutive even numbers, one must be slightly less than the mean (63), and the other slightly greater. The even number immediately less than 63 is 62, and the even number immediately greater is 64. Thus, we arrive at the same solution: 62 and 64.
This method offers a quick and insightful way to solve the problem, highlighting the relationship between the sum, average, and the numbers themselves.
Expanding the Problem: Generalizing the Solution
Let’s generalize this problem. How can we find two consecutive even numbers that sum to any given even number, N?
Let the two consecutive even numbers be x and x + 2. Their sum is x + (x + 2) = N. Solving for x:
- 2x + 2 = N
- 2x = N - 2
- x = (N - 2) / 2
Therefore, the first even number is (N - 2) / 2, and the second is (N - 2) / 2 + 2. This formula works for any even number N. For instance, if N = 150, the two consecutive even numbers would be (150 - 2) / 2 = 74 and 74 + 2 = 76.
This generalization demonstrates the power of algebra in providing a concise solution applicable to a broader range of problems.
Exploring Variations: Consecutive Odd Numbers, or More Than Two Numbers
Let's consider variations of the problem. What if we were looking for two consecutive odd numbers whose sum is 126? The approach would be very similar. We would let x represent the first odd number, and x + 2 represent the next consecutive odd number. The equation would still be x + (x + 2) = 126, leading to the same solution (x = 62), which is, in this case, incorrect. This should show that the two numbers must be even to fulfill the criteria.
What about finding three consecutive even numbers that add up to a specific sum? Let's say the sum is 180. We can represent the three numbers as x, x + 2, and x + 4. The equation would be x + (x + 2) + (x + 4) = 180. Solving this equation would yield the three consecutive even numbers.
These variations highlight the adaptability of the algebraic approach and the importance of carefully defining the problem's parameters.
The Importance of Mathematical Reasoning
Solving this simple problem, even through intuitive methods, engages important mathematical reasoning skills:
- Pattern Recognition: Identifying the relationship between consecutive even numbers.
- Logical Deduction: Using the given information to formulate an equation or a logical sequence of guesses.
- Problem Decomposition: Breaking down a complex problem into smaller, manageable steps.
- Verification: Checking the solution to ensure its accuracy.
These skills are transferable and crucial for success not only in mathematics but also in other fields that require analytical and problem-solving abilities.
Applications in Real-World Scenarios
While finding consecutive even numbers might seem abstract, similar problem-solving strategies are applied in various real-world scenarios:
- Resource Allocation: Determining how to distribute resources evenly or efficiently.
- Inventory Management: Calculating optimal stock levels.
- Financial Planning: Modeling financial growth or debt repayment.
- Engineering Design: Calculating dimensions or material requirements.
Understanding the fundamental principles of algebra and problem-solving enhances your ability to tackle more complex challenges in these and many other areas.
Frequently Asked Questions (FAQ)
Q: Can this problem be solved without using algebra?
A: Yes, the intuitive approach (guess and check) and the arithmetic mean method provide alternative solutions. However, the algebraic method is more efficient and reliable, especially for more complex variations of the problem.
Q: What if the sum of the consecutive even numbers was odd?
A: It's impossible to find two consecutive even numbers that add up to an odd number. The sum of two even numbers is always even.
Q: How would you approach this problem with larger numbers?
A: The algebraic method remains the most efficient approach for larger numbers. The intuitive method becomes increasingly impractical.
Q: Are there other ways to solve this type of problem?
A: While the methods described above are the most common and straightforward, more advanced techniques like iteration or numerical methods could be applied, but they would be overkill for this specific problem.
Conclusion
Finding two consecutive even numbers whose sum is 126 is a seemingly simple problem, but it opens a door to a wealth of mathematical concepts and problem-solving strategies. Through algebraic manipulation, intuitive reasoning, or the use of arithmetic means, we can arrive at the solution: 62 and 64. More importantly, this problem provides a valuable opportunity to strengthen our mathematical reasoning skills, skills that are highly transferable and applicable across various disciplines. By understanding the underlying principles and exploring different approaches, we can gain a deeper appreciation for the power and elegance of mathematics. The ability to generalize the solution further underscores the utility of algebraic thinking in solving a wider range of similar problems, solidifying its importance in mathematical problem-solving.
Latest Posts
Latest Posts
-
How Do You Find Exterior Angles
Aug 29, 2025
-
Are The Opposite Sides Of A Parallelogram Congruent
Aug 29, 2025
-
Find Two Consecutive Even Numbers Whose Sum Is 126
Aug 29, 2025
-
Express The Quadratic Function In Standard Form
Aug 29, 2025
-
Is 1 3 The Same As 3 4
Aug 29, 2025
Related Post
Thank you for visiting our website which covers about Find Two Consecutive Even Numbers Whose Sum Is 126 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.