Find The Graph Of The Inequality Y 1 6x 1
faraar
Sep 15, 2025 · 5 min read
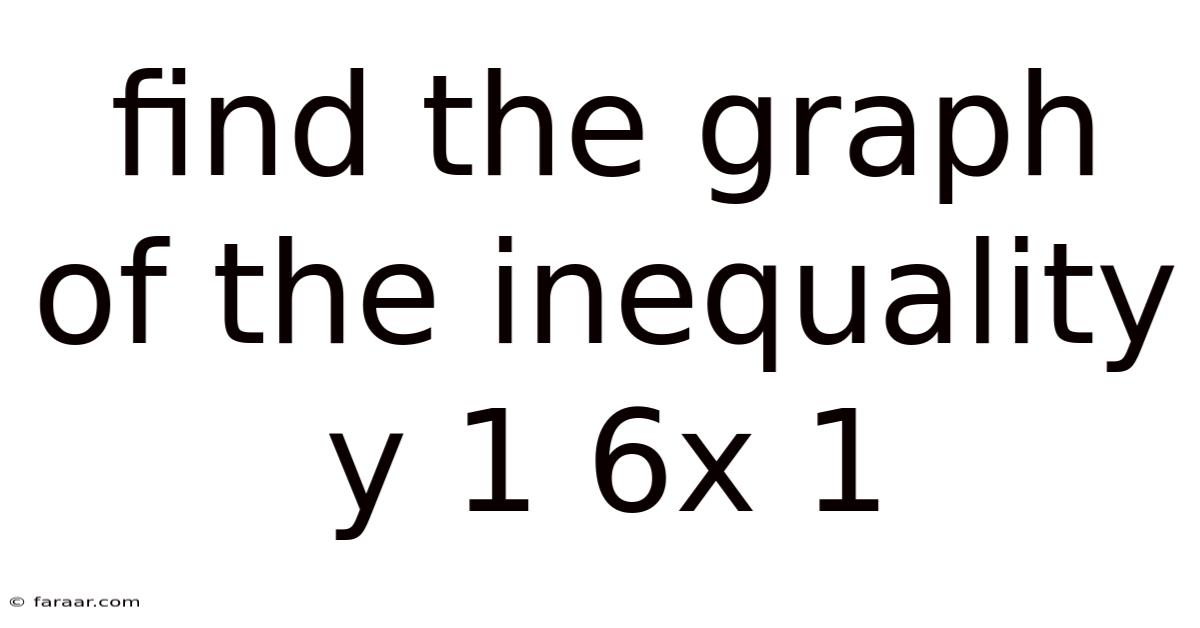
Table of Contents
Decoding the Inequality: Finding the Graph of y ≥ 6x + 1
Understanding and graphing inequalities is a crucial skill in algebra. This article will guide you through the process of finding the graph of the inequality y ≥ 6x + 1, explaining the steps involved, the underlying mathematical principles, and answering frequently asked questions. We’ll cover everything from the basics of linear inequalities to interpreting the solution set on a coordinate plane. By the end, you'll not only be able to graph this specific inequality but also confidently tackle other similar problems.
Introduction to Linear Inequalities
Before diving into the specifics of y ≥ 6x + 1, let's review the fundamental concepts of linear inequalities. A linear inequality is a mathematical statement that compares two expressions using inequality symbols: >, <, ≥, or ≤. Unlike equations, which have a single solution, inequalities typically have a range of solutions. A linear inequality in two variables (like x and y) can be represented graphically as a shaded region on the coordinate plane.
The inequality y ≥ 6x + 1 is a linear inequality because the highest power of the variables x and y is 1. The expression 6x + 1 represents a straight line, and the inequality symbol (≥) indicates that we're interested in all points above or on that line.
Steps to Graph y ≥ 6x + 1
Graphing linear inequalities involves a few key steps:
-
Graph the Boundary Line: First, treat the inequality as an equation: y = 6x + 1. This equation represents a straight line. To graph it, you can use either the slope-intercept form (y = mx + b, where m is the slope and b is the y-intercept) or find two points that satisfy the equation and connect them.
-
Slope-Intercept Method: The equation y = 6x + 1 is already in slope-intercept form. The y-intercept is 1 (the point (0, 1)), and the slope is 6 (meaning for every 1 unit increase in x, y increases by 6 units). You can plot the y-intercept and then use the slope to find another point. For example, if x = 1, y = 6(1) + 1 = 7, giving you the point (1, 7). Connect these two points to draw the line.
-
Two-Point Method: Choose any two values for x, substitute them into the equation y = 6x + 1, and solve for y. For example:
- If x = 0, y = 1. This gives the point (0, 1).
- If x = 1, y = 7. This gives the point (1, 7). Plot these points and draw a straight line through them.
-
-
Determine the Shaded Region: The inequality symbol (≥) tells us whether to shade above or below the line. Since it's "greater than or equal to," we shade the region above the line. The line itself is included in the solution set because of the "equal to" part (≥), so we draw a solid line. If the inequality was y > 6x + 1, we would use a dashed line to indicate that the line itself is not included in the solution.
-
Test a Point: To double-check your shading, choose a point not on the line and substitute its coordinates (x, y) into the inequality. If the inequality is true, shade the region containing that point; otherwise, shade the other region. A convenient point to test is the origin (0, 0).
Substituting (0, 0) into y ≥ 6x + 1: 0 ≥ 6(0) + 1 0 ≥ 1
This is false. Since (0, 0) is below the line and the inequality is false, we shade the region above the line, confirming our earlier decision.
Mathematical Explanation and Interpretations
The graph of y ≥ 6x + 1 represents the solution set of the inequality. Every point (x, y) in the shaded region satisfies the condition y ≥ 6x + 1. This means that the y-coordinate of any point in the shaded area is greater than or equal to six times the x-coordinate plus one.
The boundary line, y = 6x + 1, separates the coordinate plane into two half-planes. One half-plane contains all points that satisfy the inequality (the shaded region), and the other half-plane contains points that do not satisfy the inequality.
The slope of the line (6) represents the rate of change of y with respect to x. For every unit increase in x, y increases by 6 units. The y-intercept (1) is the point where the line crosses the y-axis.
Practical Applications
Understanding linear inequalities is crucial in various fields:
- Economics: Modeling supply and demand, resource allocation, and profit maximization.
- Business: Analyzing cost functions, optimizing production, and setting price points.
- Engineering: Designing systems with constraints and limitations.
- Computer Science: Linear programming and optimization algorithms.
Frequently Asked Questions (FAQ)
-
What if the inequality was y < 6x + 1? The process would be the same, but you would shade the region below the line, and the line itself would be a dashed line (because the points on the line are not included in the solution).
-
How do I graph inequalities with different inequality symbols? The inequality symbol determines whether the line is solid or dashed and which region to shade:
- > or <: Dashed line
- ≥ or ≤: Solid line
- >: Shade above the line
- <: Shade below the line
- ≥: Shade above the line, including the line itself.
- ≤: Shade below the line, including the line itself.
-
What if the inequality is not in slope-intercept form? You can rearrange the inequality to solve for y and then follow the steps outlined above. For example, if you have 2x - y ≤ 4, you would rearrange it to y ≥ 2x - 4.
-
Can I use graphing software to verify my graph? Yes, many graphing calculators and online tools can graph linear inequalities, allowing you to check your work.
Conclusion
Graphing the inequality y ≥ 6x + 1 involves understanding the concepts of linear inequalities, plotting the boundary line, determining the shaded region, and testing a point to verify your solution. The resulting graph represents the set of all points (x, y) that satisfy the inequality. This fundamental skill is applicable across numerous fields, highlighting the importance of mastering linear inequality graphing. Remember to practice with different inequalities to solidify your understanding and build confidence in tackling more complex problems. By understanding the underlying principles and following the steps carefully, you can successfully graph any linear inequality and confidently interpret its solution set.
Latest Posts
Latest Posts
-
Use Synthetic Division To Find The Quotient And The Remainder
Sep 15, 2025
-
How Do You Find The Gradient Of A Function
Sep 15, 2025
-
C 85x 60 Solve For X
Sep 15, 2025
-
A Small Mailbag Is Released From A Helicopter
Sep 15, 2025
-
Solve Each Triangle Round To The Nearest Tenth
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Find The Graph Of The Inequality Y 1 6x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.