C 85x 60 Solve For X
faraar
Sep 15, 2025 · 5 min read
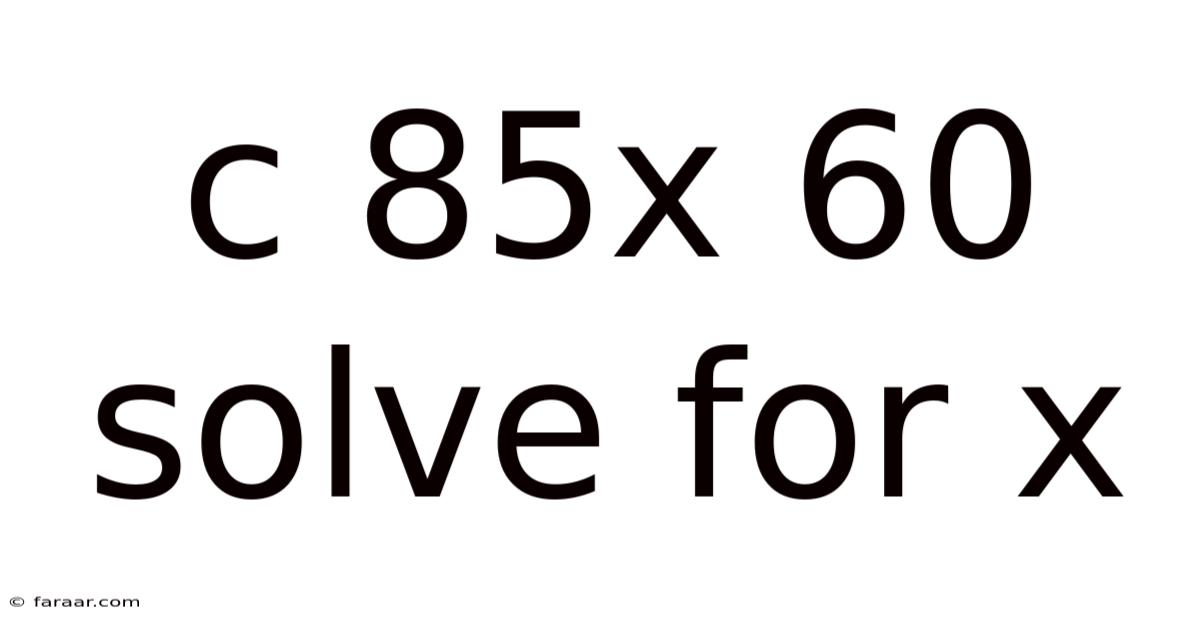
Table of Contents
Solving for x: A Deep Dive into the Equation C = 85x + 60
This article provides a comprehensive guide to solving the equation C = 85x + 60 for x. We'll explore various approaches, delve into the underlying mathematical concepts, and consider practical applications. Understanding this seemingly simple equation can unlock valuable skills in algebra and problem-solving, applicable across numerous fields. We'll also address common questions and misconceptions.
Introduction: Understanding Linear Equations
The equation C = 85x + 60 is a linear equation. This means that when graphed, it forms a straight line. Linear equations are fundamental in mathematics and have countless real-world applications, from calculating costs and profits to modeling population growth and predicting future trends. The equation itself represents a relationship between two variables, C and x. 'C' represents a total cost, 'x' represents a quantity (e.g., number of items, units of time), 85 represents the cost per unit of x, and 60 represents a fixed cost (e.g., a setup fee or initial investment). Our goal is to isolate 'x', meaning we want to find an expression that tells us the value of x given a specific value of C.
Methods for Solving for x
There are several ways to solve for x in the equation C = 85x + 60. We'll explore two primary methods:
1. Using Inverse Operations:
This method involves systematically undoing the operations performed on x. The order of operations (PEMDAS/BODMAS) guides us; we perform the inverse operations in the reverse order.
-
Step 1: Subtract 60 from both sides:
The equation is currently C = 85x + 60. To isolate the term with x, we subtract 60 from both sides of the equation to maintain balance:
C - 60 = 85x + 60 - 60
This simplifies to:
C - 60 = 85x
-
Step 2: Divide both sides by 85:
Now, x is multiplied by 85. To isolate x, we divide both sides of the equation by 85:
(C - 60) / 85 = 85x / 85
This simplifies to:
x = (C - 60) / 85
Therefore, the solution for x is: x = (C - 60) / 85
This formula allows you to calculate the value of x for any given value of C.
2. Using Algebraic Manipulation:
This method involves rearranging the equation through equivalent transformations to explicitly solve for x. The principle is to perform operations that maintain the equality of the equation.
-
Begin with the original equation: C = 85x + 60
-
Subtract 60 from both sides: C - 60 = 85x
-
Divide both sides by 85: (C - 60) / 85 = x
-
Rearrange the equation: x = (C - 60) / 85
This approach arrives at the same solution as the inverse operations method, highlighting the flexibility of algebraic manipulation.
Illustrative Examples
Let's apply the formula to understand its practical use.
-
Example 1: Finding x when C = 205
Substitute C = 205 into the formula: x = (205 - 60) / 85 = 145 / 85 = 1.71 (approximately).
-
Example 2: Finding x when C = 1000
Substitute C = 1000 into the formula: x = (1000 - 60) / 85 = 940 / 85 = 11.06 (approximately).
Explanation of the Equation's Components
Let's break down the meaning of each component of the equation C = 85x + 60 in a real-world context. Imagine a company manufacturing widgets:
-
C: Represents the total cost of producing a batch of widgets.
-
85: Represents the variable cost per widget (e.g., materials, labor directly involved in widget production).
-
x: Represents the number of widgets produced.
-
60: Represents the fixed costs (e.g., rent, utilities, salaries of administrative staff – costs incurred regardless of the number of widgets produced).
Therefore, the equation models the total cost (C) as a function of the number of widgets produced (x). The fixed cost is always present, while the variable cost increases proportionally with the number of widgets.
Practical Applications
The equation C = 85x + 60, and the ability to solve it for x, has wide-ranging applications across diverse fields:
-
Business and Economics: Cost analysis, profit maximization, break-even point calculation, pricing strategies.
-
Engineering: Cost estimation for projects, resource allocation.
-
Finance: Calculating interest, predicting investment returns.
-
Science: Modeling linear relationships between variables in experiments and observations.
Frequently Asked Questions (FAQ)
-
What if C is less than 60? If C < 60, then the solution for x will be negative. This indicates that the equation, as a model of cost, doesn't apply to values of C below the fixed cost. It implies that you wouldn't be able to produce any widgets with less than the fixed cost.
-
What are the limitations of this model? This linear model assumes a constant cost per unit (85) and a constant fixed cost (60). In reality, costs may fluctuate due to economies of scale, inflation, or other factors. The model may not be accurate over extremely wide ranges of x.
-
Can this equation be used for other scenarios? Absolutely! The equation's structure (C = mx + b, where 'm' is the slope and 'b' is the y-intercept) is a general form of a linear equation applicable to various situations where a linear relationship exists between two variables. Just change the values of 'm' and 'b' to represent the specific situation.
-
What if the equation was more complex? More complex equations might involve multiple variables or non-linear relationships, requiring more advanced algebraic techniques for solving.
Conclusion: Mastering Linear Equations
Solving the equation C = 85x + 60 for x is a fundamental skill in algebra. Mastering this skill not only enhances your mathematical abilities but also provides you with valuable tools for problem-solving across various disciplines. By understanding the underlying concepts and applying the methods outlined above, you can confidently tackle similar linear equations and unlock the power of mathematical modeling in real-world scenarios. Remember, practice is key – the more you work with these equations, the more comfortable and proficient you'll become. This foundational knowledge forms the bedrock for more advanced mathematical concepts and applications.
Latest Posts
Latest Posts
-
What Is The Diameter Of A 12 Inch Circle
Sep 15, 2025
-
Formula For Thickness Of Aluminum Foil
Sep 15, 2025
-
Surface Area Of A Pentagonal Pyramid
Sep 15, 2025
-
What Phylum Do Humans Belong To
Sep 15, 2025
-
Simplify The Difference Quotient By Rationalizing The Numerator
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about C 85x 60 Solve For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.