Does 1/4 And 1/4 Equal 1/2
faraar
Sep 10, 2025 · 6 min read
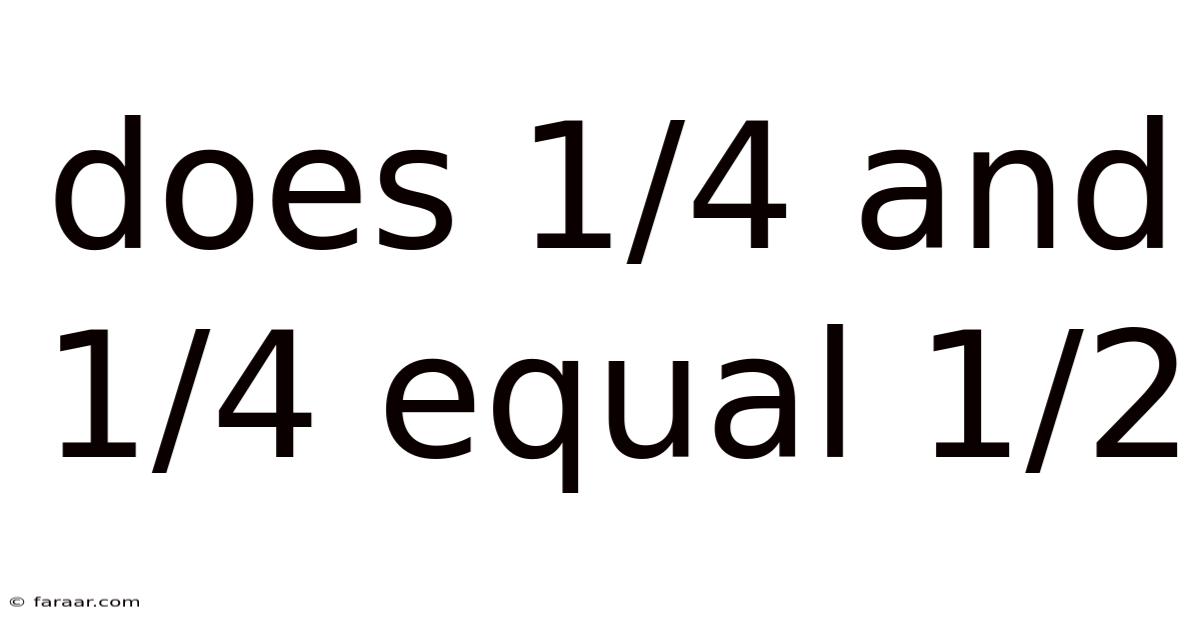
Table of Contents
Does 1/4 + 1/4 Equal 1/2? A Deep Dive into Fraction Addition
Understanding fractions is a cornerstone of mathematics, forming the basis for more advanced concepts in algebra, calculus, and beyond. A seemingly simple question like "Does 1/4 + 1/4 equal 1/2?" often trips up students, highlighting the importance of grasping the fundamentals of fraction addition. This article will not only answer this question definitively but also delve into the underlying principles, providing a comprehensive understanding of how to add fractions and why this specific addition holds true. We'll explore the concept of common denominators, visualize the process, and address common misconceptions. By the end, you'll confidently tackle similar fraction problems and appreciate the elegance of this fundamental mathematical operation.
Understanding Fractions: A Quick Recap
Before jumping into the addition, let's refresh our understanding of what fractions represent. A fraction, like 1/4, signifies a part of a whole. The number on top, the numerator, indicates how many parts we have. The number on the bottom, the denominator, indicates the total number of equal parts the whole is divided into. So, 1/4 means we have one part out of a total of four equal parts.
Imagine a pizza cut into four equal slices. 1/4 represents one slice of that pizza. If you have another slice, you have a total of two slices. This is where the addition comes in.
Adding Fractions: The Crucial Role of Common Denominators
The key to adding fractions lies in understanding the concept of a common denominator. When adding fractions, the denominators must be the same. This is because you can only directly add parts of a whole that are of the same size. You can't directly add one quarter of a pizza to one third of a pizza because the slices are different sizes.
In our example, 1/4 + 1/4, the denominators are already the same (both are 4). This makes the addition straightforward.
Calculating 1/4 + 1/4
Since the denominators are the same, we simply add the numerators and keep the denominator unchanged.
1/4 + 1/4 = (1 + 1) / 4 = 2/4
Now we have the result 2/4. But is this the simplest form? Not quite.
Simplifying Fractions: Finding the Lowest Common Denominator (LCD)
Often, a fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
In the case of 2/4, both 2 and 4 are divisible by 2. Dividing both the numerator and denominator by 2 gives:
2/4 = (2 ÷ 2) / (4 ÷ 2) = 1/2
Therefore, 1/4 + 1/4 = 2/4 = 1/2
Visualizing the Addition: A Concrete Example
Let's visualize this using the pizza analogy. Imagine you have a pizza cut into four equal slices. You take one slice (1/4) and then take another slice (1/4). Together, you have two slices out of four (2/4), which is equivalent to half the pizza (1/2). This visual representation reinforces the mathematical calculation.
Addressing Common Misconceptions
Many students struggle with fraction addition due to a few common misconceptions:
-
Adding denominators: A frequent mistake is adding both the numerators and the denominators. This is incorrect. Remember, you only add the numerators when the denominators are the same; the denominator remains unchanged.
-
Incorrect simplification: After adding fractions, ensure the result is simplified to its lowest terms. Failing to do so results in an incomplete or less precise answer.
-
Difficulty with unlike denominators: Adding fractions with unlike denominators requires finding a common denominator before adding the numerators. This involves finding the least common multiple (LCM) of the denominators.
Adding Fractions with Unlike Denominators: A Step-by-Step Guide
Let's illustrate adding fractions with unlike denominators. Suppose we want to calculate 1/3 + 1/2.
-
Find the least common denominator (LCD): The LCD is the smallest number that is a multiple of both denominators (3 and 2). The LCM of 3 and 2 is 6.
-
Convert fractions to equivalent fractions with the LCD: We need to rewrite both fractions with a denominator of 6.
- 1/3 can be rewritten as 2/6 (multiply both numerator and denominator by 2)
- 1/2 can be rewritten as 3/6 (multiply both numerator and denominator by 3)
-
Add the numerators: Now that the denominators are the same, we add the numerators:
2/6 + 3/6 = (2 + 3) / 6 = 5/6
Therefore, 1/3 + 1/2 = 5/6.
The Importance of Mastering Fraction Addition
Mastering fraction addition is crucial for various reasons:
-
Foundation for higher mathematics: Fraction addition forms the bedrock for more advanced mathematical concepts such as algebra, calculus, and even statistics.
-
Real-world applications: Fractions are used extensively in everyday life, from cooking and baking to measuring ingredients and calculating proportions. Understanding fraction addition allows you to accurately perform these calculations.
-
Problem-solving skills: Working with fractions hones your problem-solving skills, teaching you to break down complex problems into manageable steps.
-
Critical thinking: Understanding the principles behind fraction addition encourages critical thinking and attention to detail.
Frequently Asked Questions (FAQs)
Q: What if the fractions have different denominators?
A: If the fractions have different denominators, you must first find the least common denominator (LCD) and convert the fractions to equivalent fractions with that denominator before adding the numerators.
Q: How do I simplify a fraction?
A: To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD.
Q: Can I add fractions with different denominators directly?
A: No, you cannot add fractions directly if they have different denominators. You must first find a common denominator.
Q: Why is finding the least common denominator (LCD) important?
A: Finding the LCD ensures that you are adding parts of the whole that are of the same size, leading to an accurate result. Using any common denominator will work, but the LCD simplifies the calculation.
Q: What happens if the result is an improper fraction (numerator larger than the denominator)?
A: If the result is an improper fraction, you can convert it to a mixed number (a whole number and a fraction). For example, 7/4 can be converted to 1 3/4.
Conclusion
The answer to the question "Does 1/4 + 1/4 equal 1/2?" is a resounding yes. This simple addition highlights the fundamental principles of fraction addition: the importance of common denominators, the process of adding numerators while keeping the denominator consistent, and the crucial step of simplifying the result to its lowest terms. By understanding these principles and practicing regularly, you will build a strong foundation in mathematics, opening doors to more complex concepts and real-world applications. Remember, fractions are more than just numbers; they are representations of parts of a whole, and understanding their manipulation is key to solving various mathematical problems. Continue practicing, and you'll find that mastering fractions becomes increasingly intuitive and rewarding.
Latest Posts
Latest Posts
-
How To Factor Out Square Roots
Sep 10, 2025
-
4 3 Divided By 1 2 As A Fraction
Sep 10, 2025
-
Use The Given Values To Complete Each Table
Sep 10, 2025
-
Calculate The Theoretical Yield Of Carbon Dioxide
Sep 10, 2025
-
What Is The Value Of 3 3
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Does 1/4 And 1/4 Equal 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.