What Is The Value Of 3 3
faraar
Sep 10, 2025 · 6 min read
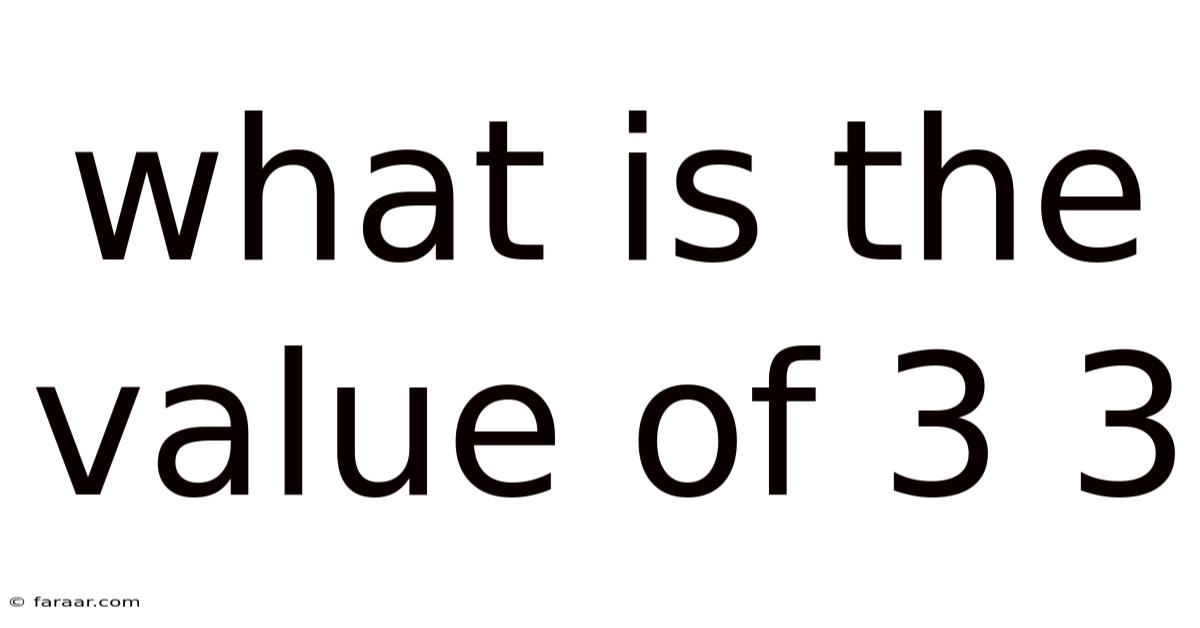
Table of Contents
Decoding the Value of "3 3": Exploring Mathematical Notation and Its Interpretations
The seemingly simple expression "3 3" might initially appear straightforward, but its true value depends entirely on the context and the implied mathematical operation. This article delves into the various interpretations of "3 3," explaining the importance of mathematical notation, exploring different operations, and clarifying the ambiguities that can arise when mathematical symbols are used without sufficient context. Understanding these nuances is crucial for accurate mathematical communication and problem-solving. We'll explore scenarios ranging from basic arithmetic to more advanced mathematical concepts, ultimately clarifying the value of "3 3" depending on the intended operation.
Introduction: The Importance of Precise Mathematical Notation
Mathematics relies heavily on precise notation. The symbols we use – numbers, operators, parentheses, etc. – are not arbitrary; they carry specific meanings. A slight change in notation can drastically alter the result of a calculation. The expression "3 3," without further specification, is inherently ambiguous. It lacks the crucial element of an operator – the symbol indicating the mathematical operation to be performed. This ambiguity highlights the importance of clearly defining the operation intended when writing mathematical expressions.
Possible Interpretations and Their Values
Let's explore the most common interpretations of "3 3" and determine their corresponding values:
1. Addition: 3 + 3
The most straightforward interpretation is addition. In this case, "3 3" implies "3 + 3." The value is simply the sum of the two numbers:
3 + 3 = 6
This is the most likely interpretation if the expression appears in a basic arithmetic context.
2. Subtraction: 3 - 3
Subtraction is another fundamental arithmetic operation. If the expression implies subtraction, we would have:
3 - 3 = 0
This scenario yields a different result compared to addition, highlighting the significance of correctly identifying the operation.
3. Multiplication: 3 × 3
Multiplication is a more advanced operation than addition and subtraction. Interpreting "3 3" as multiplication would mean "3 × 3," resulting in:
3 × 3 = 9
This interpretation produces a significantly different outcome from addition and subtraction, demonstrating how the choice of operation dramatically impacts the final result.
4. Division: 3 ÷ 3
Division is another crucial arithmetic operation. If we interpret "3 3" as division, it becomes "3 ÷ 3," leading to:
3 ÷ 3 = 1
This reveals yet another distinct value, reinforcing the necessity of clear mathematical notation.
5. Exponentiation: 3³
Exponentiation represents repeated multiplication. If "3 3" represents 3 raised to the power of 3 (3 cubed), the calculation is:
3³ = 3 × 3 × 3 = 27
This outcome showcases a substantially larger value compared to the previous operations, demonstrating the significant impact of selecting the correct operation.
6. Concatenation (in certain contexts)
In some programming languages or contexts involving string manipulation, "3 3" could represent string concatenation. This would mean joining the two "3"s together to form a single string:
"3 3" (concatenation) = "33"
The result is the string "33," which has a different meaning altogether; it is no longer a numerical value but a textual representation.
The Role of Context in Determining Value
The examples above demonstrate the critical role of context in determining the value of "3 3." The intended operation must be explicitly stated or clearly implied from the surrounding mathematical context. Without this clarification, the expression remains ambiguous and can lead to multiple, potentially contradictory, interpretations.
For instance, if "3 3" appears within a problem involving repeated multiplication, exponentiation is the most probable interpretation. Conversely, if the problem deals solely with basic arithmetic, addition or subtraction would be more likely. The surrounding mathematical expressions and the nature of the problem should provide sufficient clues to decipher the intended operation.
Expanding the Discussion: Advanced Mathematical Concepts
While the basic arithmetic interpretations dominate in simple scenarios, more advanced mathematical concepts can also come into play depending on the context. For instance:
-
Matrices: In linear algebra, "3 3" might represent a 3x3 matrix, a fundamental concept in matrix operations. The value, in this case, wouldn't be a single number but a collection of numbers arranged in a specific structure.
-
Vectors: Similarly, "3 3" could represent a 3-dimensional vector in vector algebra. The value would be a vector in three-dimensional space, described by its components.
-
Set Theory: In set theory, "3 3" might be a shorthand, albeit unconventional, notation relating to sets with cardinality 3. However, this is a less common interpretation.
-
Tensors: In advanced physics and engineering, "3 3" could denote components of tensors, high-dimensional arrays of numbers. Again, the “value” would be a complex mathematical object rather than a single number.
These advanced applications underscore the pervasive ambiguity inherent in the expression “3 3” unless sufficient context is provided.
Addressing Potential Ambiguities: The Power of Parentheses and Explicit Operators
To avoid ambiguity and ensure clarity in mathematical communication, it's essential to utilize parentheses and explicitly state the operation intended. For example:
- Addition: (3 + 3)
- Subtraction: (3 - 3)
- Multiplication: (3 × 3)
- Division: (3 ÷ 3)
- Exponentiation: (3³)
Using parentheses prevents any misunderstanding and eliminates multiple interpretations. Moreover, always write the operator explicitly to avoid confusion. Instead of "3 3," use "3 + 3," "3 - 3," "3 × 3," "3 ÷ 3," or "3³." This practice significantly enhances the clarity and accuracy of mathematical expressions.
Frequently Asked Questions (FAQ)
Q: What is the most likely interpretation of "3 3" in a basic arithmetic context?
A: In a basic arithmetic context, the most likely interpretation is addition (3 + 3 = 6).
Q: Why is precise mathematical notation crucial?
A: Precise notation is crucial because it ensures that mathematical expressions are unambiguous and have only one correct interpretation. Without precision, confusion and errors can easily arise.
Q: Can "3 3" have multiple values?
A: Yes, "3 3" can have multiple values depending on the intended mathematical operation. This highlights the necessity of clearly specifying the operation being performed.
Q: How can I avoid ambiguity when writing mathematical expressions?
A: Always use parentheses to group terms and clearly state the operation (e.g., +, -, ×, ÷, ^) to remove any uncertainty.
Q: What if the context isn't clear?
A: If the context isn't clear, you should seek clarification. Assume nothing. Ask for the intended operation to be explicitly stated before attempting to solve the problem.
Conclusion: The Value of Clarity in Mathematics
The seemingly trivial question of "What is the value of 3 3?" reveals a fundamental principle in mathematics: the paramount importance of precise notation and clear communication. Without specifying the mathematical operation, the expression remains ambiguous, leading to multiple possible interpretations. The value, therefore, is not inherent to "3 3" itself but entirely dependent on the context and the operation intended. Always prioritize clarity in mathematical writing by using parentheses and explicitly stating the operators to prevent misinterpretations and ensure accurate calculations. This practice is crucial for effective mathematical communication and problem-solving, regardless of the complexity of the expressions involved. Remember, in mathematics, precision is paramount.
Latest Posts
Latest Posts
-
French Horn Private Lessons Near Me
Sep 10, 2025
-
How Much Does Abc Plumbing Cost
Sep 10, 2025
-
Why Were Scribes Important In Sumerian Society
Sep 10, 2025
-
There Are Integers That Are Not Rational Numbers
Sep 10, 2025
-
For Parallelogram Abcd Find The Value Of X
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of 3 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.