60 Of What Number Is 30
faraar
Sep 23, 2025 · 5 min read
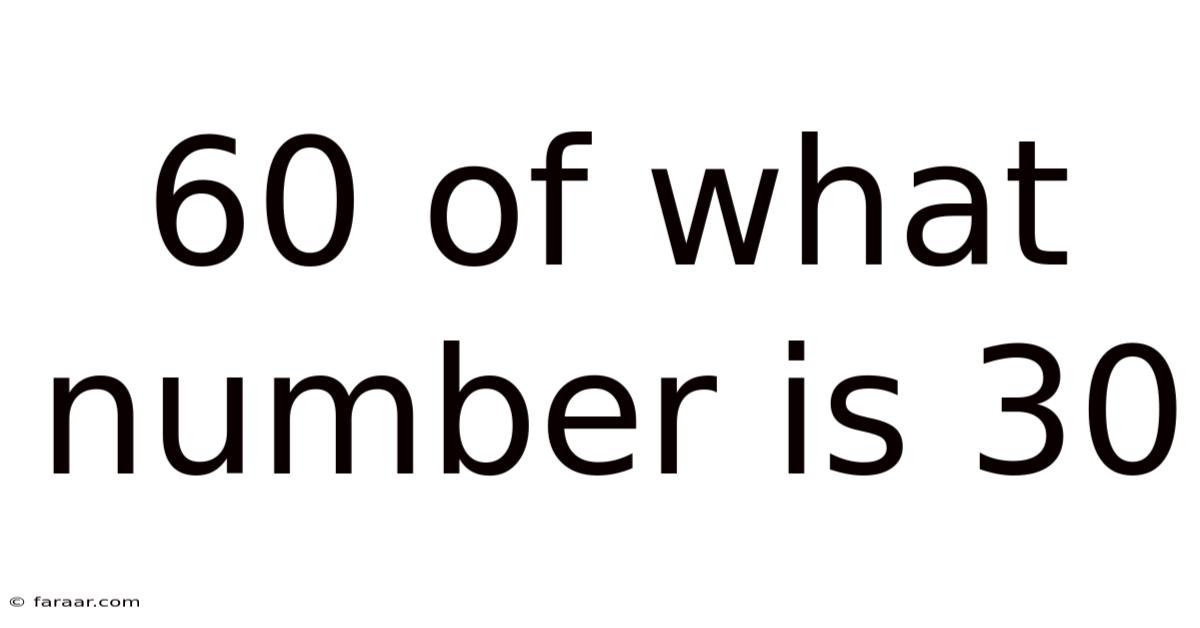
Table of Contents
60% of What Number is 30? Understanding Percentages and Problem Solving
This article delves into the seemingly simple question: "60% of what number is 30?" While the answer might seem immediately apparent to some, understanding the underlying mathematical principles and exploring different solution methods is crucial for developing a strong grasp of percentages and problem-solving skills. We'll unpack this problem, exploring various approaches, including algebraic solutions and practical applications, ensuring a comprehensive understanding for learners of all levels.
Understanding Percentages
Before diving into the solution, let's solidify our understanding of percentages. A percentage is a fraction expressed as a number out of 100. For instance, 60% can be written as 60/100 or its simplified form, 3/5. This means that 60% represents 60 parts out of a total of 100 equal parts. Understanding this fundamental concept is key to solving percentage problems effectively. We often use percentages to represent proportions, ratios, or changes in value. For example, a 10% discount on an item means you pay 90% of the original price.
Method 1: Algebraic Approach
This is the most common and arguably most robust method for solving percentage problems. We'll translate the problem into an algebraic equation. Let's represent the unknown number as 'x'. The problem can be expressed as:
0.60 * x = 30
Here, 0.60 represents 60% as a decimal (obtained by dividing 60 by 100). To solve for 'x', we simply isolate it by dividing both sides of the equation by 0.60:
x = 30 / 0.60
x = 50
Therefore, 60% of 50 is 30.
Method 2: Using Proportions
Proportions offer an alternative approach, particularly helpful for visualizing the relationship between the known and unknown quantities. We can set up a proportion as follows:
60/100 = 30/x
This proportion states that the ratio of 60 to 100 is equal to the ratio of 30 to the unknown number (x). To solve for x, we cross-multiply:
60 * x = 30 * 100
60x = 3000
x = 3000 / 60
x = 50
Again, we find that x = 50. This method reinforces the concept of equivalent ratios and provides a visual representation of the problem.
Method 3: Working with Fractions
Since 60% is equivalent to the fraction 3/5, we can also solve the problem using fractions. The problem becomes:
(3/5) * x = 30
To solve for x, we multiply both sides by the reciprocal of 3/5, which is 5/3:
x = 30 * (5/3)
x = (30 * 5) / 3
x = 150 / 3
x = 50
This method highlights the interchangeability between percentages, decimals, and fractions, further strengthening the understanding of these mathematical concepts.
Practical Applications
Understanding how to solve percentage problems like "60% of what number is 30?" has widespread practical applications in various real-world scenarios:
- Sales and Discounts: Calculating the original price of an item after a discount. For example, if an item is on sale for 30 after a 60% discount, the original price was 50.
- Finance and Investments: Determining the initial investment amount based on a percentage return. If an investment yielded a 60% return of 30, the initial investment was 50.
- Statistics and Data Analysis: Calculating the total population based on a percentage representing a specific subgroup. If 60% of a population is 30,000 people, the total population is 50,000.
- Science and Engineering: Scaling measurements or quantities based on percentage changes. For example, if a material shrinks by 60% resulting in a 30cm length, the original length was 50cm.
Expanding the Understanding: Variations and Extensions
Let’s explore some variations of the problem to solidify our understanding:
- What is 60% of 50? This is a straightforward calculation: 0.60 * 50 = 30. This helps to understand the inverse relationship between the two problems.
- What percentage of 50 is 30? This problem requires calculating the percentage: (30/50) * 100 = 60%.
- 30 is what percentage of 75? This problem necessitates calculating the percentage: (30/75) * 100 = 40%.
- Solving problems with different percentages: The methods discussed can be readily applied to solve similar problems with varying percentages, such as "75% of what number is 60?" or "25% of what number is 10?".
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Absolutely! Calculators can simplify the numerical calculations, particularly when dealing with more complex percentage problems. However, it's crucial to understand the underlying mathematical principles to apply the correct formulas and interpret the results accurately.
Q: What if the percentage is not a whole number?
A: The methods remain the same. You would simply use the decimal equivalent of the percentage in the calculations. For example, if the problem was "33.33% of what number is 10?", you'd use 0.3333 in your calculations.
Q: Why are there multiple ways to solve this problem?
A: Different approaches cater to various learning styles and preferences. Understanding multiple methods provides a more robust grasp of the concepts and allows you to choose the most suitable method for a given problem.
Q: Are there any online tools or resources to help me practice?
A: Many websites and educational platforms offer online resources, including practice problems and interactive exercises, to help you improve your skills in solving percentage problems.
Conclusion
Solving the problem "60% of what number is 30?" is not merely about obtaining the answer (which is 50). It's about grasping the fundamental concepts of percentages, decimals, fractions, and algebraic problem-solving. Through understanding various solution methods and their practical applications, you enhance your mathematical proficiency and develop skills applicable across numerous fields. The journey from a seemingly simple question to a comprehensive understanding of percentages is a valuable exercise in mathematical reasoning and critical thinking. Remember to practice various problems and explore different methods to solidify your understanding and build confidence in tackling more challenging percentage calculations in the future. By consistently applying these principles, you'll develop a robust and versatile approach to solving a wide variety of percentage problems.
Latest Posts
Latest Posts
-
Using Algebra In The Real World
Sep 23, 2025
-
How Do I Learn To Spell Better
Sep 23, 2025
-
Find The Fundamental Set Of Solutions For The Differential Equation
Sep 23, 2025
-
Mean Free Path Of An Electron
Sep 23, 2025
-
What Is 20 Percent Off 60 Dollars
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 60 Of What Number Is 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.