Consider The Differential Equation Dy Dx Y 1 X 2
faraar
Sep 20, 2025 · 7 min read
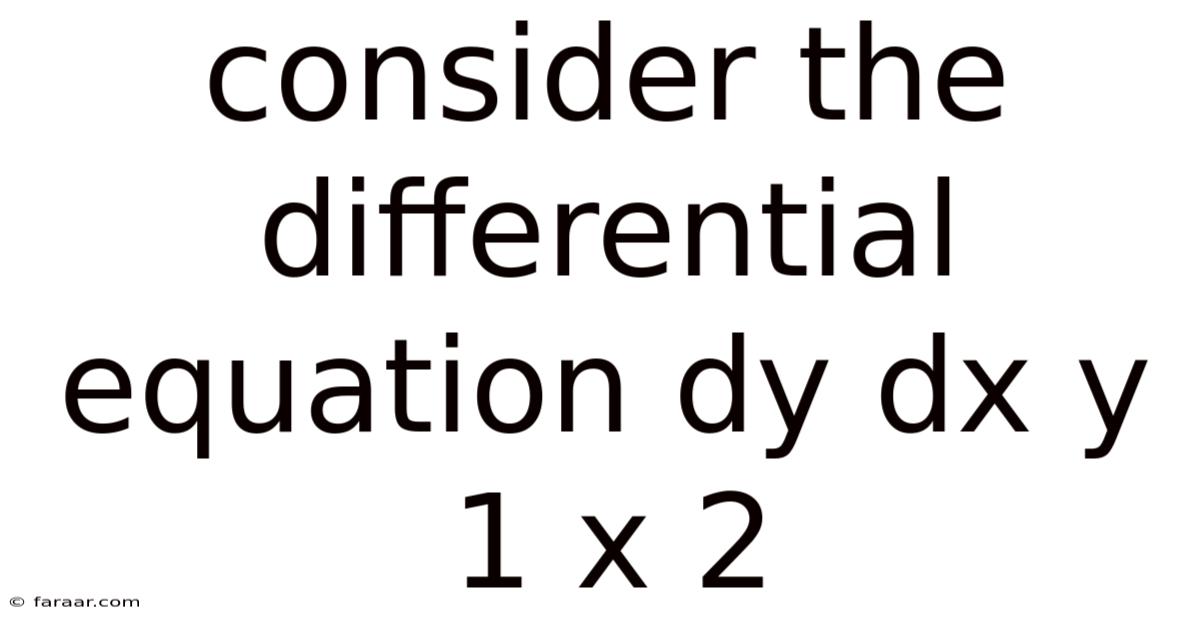
Table of Contents
Exploring the Differential Equation: dy/dx = y + 1/x²
This article delves into the fascinating world of differential equations, specifically focusing on the equation dy/dx = y + 1/x². We'll explore its solution, different approaches to solving it, and the underlying mathematical concepts. This equation, while seemingly simple, offers a rich learning opportunity in understanding techniques for solving first-order linear differential equations. Understanding this equation provides a solid foundation for tackling more complex differential equations encountered in various fields like physics, engineering, and finance.
Introduction: Understanding First-Order Linear Differential Equations
Before diving into the solution, let's establish the context. The given equation, dy/dx = y + 1/x², is a first-order linear differential equation. This means:
- First-order: The highest derivative present is the first derivative (dy/dx).
- Linear: The dependent variable (y) and its derivative appear only to the first power and are not multiplied together.
This specific structure allows us to employ specific techniques for finding its solution. The general form of a first-order linear differential equation is:
dy/dx + P(x)y = Q(x)
where P(x) and Q(x) are functions of x. Our equation needs slight rearrangement to fit this form.
Rearranging the Equation into Standard Form
To solve our equation, dy/dx = y + 1/x², we first need to rewrite it in the standard form of a first-order linear differential equation:
dy/dx - y = 1/x²
Now we can clearly identify P(x) = -1 and Q(x) = 1/x². This form allows us to apply the method of integrating factors.
Solving using the Integrating Factor Method
The integrating factor method is a powerful technique for solving first-order linear differential equations. The integrating factor (IF) is defined as:
IF = e^(∫P(x)dx)
In our case, P(x) = -1, so the integrating factor is:
IF = e^(∫-1 dx) = e^(-x)
Next, we multiply both sides of the rearranged equation by the integrating factor:
e^(-x) (dy/dx - y) = e^(-x) (1/x²)
The left-hand side is now the derivative of a product:
d/dx [e^(-x)y] = e^(-x) / x²
Now, we integrate both sides with respect to x:
∫d/dx [e^(-x)y] dx = ∫e^(-x) / x² dx
This simplifies to:
e^(-x)y = ∫e^(-x) / x² dx
The integral on the right-hand side, ∫e^(-x) / x² dx, is not expressible in terms of elementary functions. This means we cannot find a closed-form solution using elementary functions. We can, however, express the solution using an integral:
y = e^x ∫e^(-x) / x² dx + Ce^x
where C is the constant of integration.
Understanding the Non-Elementary Integral
The integral ∫e^(-x) / x² dx is a crucial part of the solution. It represents a special function that doesn't have a simple representation using common functions like polynomials, exponentials, or trigonometric functions. This integral can be approximated using numerical methods or expressed using special functions like the exponential integral (Ei(x)).
This highlights an important aspect of solving differential equations: not all solutions will have neat, closed-form expressions. The presence of this non-elementary integral underscores the complexity that can arise even in seemingly simple differential equations.
Numerical Methods for Approximation
Since a closed-form solution using elementary functions is not possible, we can resort to numerical methods to approximate the solution. These methods provide numerical values of y for specific values of x. Common numerical methods include:
- Euler's Method: A simple but less accurate method for approximating solutions.
- Improved Euler's Method (Heun's Method): An improvement over Euler's method, offering better accuracy.
- Runge-Kutta Methods: A family of more sophisticated methods providing higher accuracy.
These methods involve iterative calculations, starting from an initial condition (a specific value of y at a particular x), and progressively approximating the solution at subsequent points.
Exploring Initial Conditions and Specific Solutions
The constant of integration, C, in the solution y = e^x ∫e^(-x) / x² dx + Ce^x, represents the family of solutions to the differential equation. To obtain a specific solution, we need an initial condition. An initial condition is a point (x₀, y₀) that the solution must pass through. For example:
If the initial condition is y(1) = 2, we can substitute x = 1 and y = 2 into the general solution to determine the value of C. However, due to the non-elementary integral, finding the exact value of C would require numerical methods to approximate the integral.
Alternative Approaches and Considerations
While the integrating factor method is effective for this type of equation, other approaches could be explored, albeit likely with similar challenges regarding the non-elementary integral:
- Laplace Transforms: This method can be applied to some differential equations, but the presence of 1/x² might introduce complexities in the inverse Laplace transform.
- Series Solutions: We could attempt to find a series solution to the differential equation, representing the solution as an infinite series. This approach often yields approximate solutions valid within a certain range of x.
Applications and Significance
Differential equations of this type frequently appear in various applications, including:
- Physics: Modeling the decay of radioactive substances, or the cooling of an object.
- Engineering: Analyzing circuits, modeling mechanical systems, or predicting the behaviour of structures.
- Finance: Pricing options, modeling interest rates, or evaluating investment strategies.
Understanding the solution methods and limitations, as illustrated by this equation, is crucial for building robust and accurate models in these fields.
Frequently Asked Questions (FAQ)
Q1: Why is the integral ∫e^(-x) / x² dx non-elementary?
A1: This integral is non-elementary because there's no combination of elementary functions (polynomials, exponentials, trigonometric functions, etc.) that can be differentiated to yield e^(-x) / x². It represents a special function that requires numerical approximation or representation using special functions like the exponential integral.
Q2: Can we solve this equation without using the integrating factor method?
A2: While other methods exist (Laplace transforms, series solutions), they will likely encounter the same challenge related to the non-elementary integral. The integrating factor method is arguably the most straightforward approach for first-order linear differential equations of this type.
Q3: What does the constant of integration, C, represent?
A3: The constant of integration, C, represents the family of solutions to the differential equation. Each value of C corresponds to a specific solution curve. An initial condition is required to determine the value of C and obtain a unique solution.
Q4: How accurate are numerical methods for approximating the solution?
A4: The accuracy of numerical methods depends on the method used and the step size chosen. More sophisticated methods like Runge-Kutta methods generally offer higher accuracy compared to simpler methods like Euler's method. The accuracy can be improved by decreasing the step size, but this increases the computational cost.
Q5: Are there similar differential equations that are easier to solve?
A5: Yes, many first-order linear differential equations have simpler solutions if Q(x) leads to an elementary integral after applying the integrating factor. For instance, if Q(x) were a simpler function like x or e^x, the resulting integral would be elementary, and a closed-form solution would be readily obtainable.
Conclusion: A Journey into the World of Differential Equations
This exploration of the differential equation dy/dx = y + 1/x² provides a valuable insight into the techniques and challenges involved in solving differential equations. The presence of a non-elementary integral in the solution highlights the fact that not all differential equations yield solutions expressible in terms of elementary functions. Understanding this limitation and employing numerical methods for approximation are essential skills for anyone working with differential equations in various scientific and engineering disciplines. This seemingly simple equation serves as a powerful example demonstrating the interplay between analytical and numerical approaches in solving differential equations and underscores the richness and complexity inherent in this branch of mathematics.
Latest Posts
Latest Posts
-
The Era Of Good Feelings Was So Called Because
Sep 20, 2025
-
5 1 3 2 2 3
Sep 20, 2025
-
Domain Of X 2 X 1
Sep 20, 2025
-
Solve For X Assume That Lines Which Appear Tangent
Sep 20, 2025
-
A Pile Of Coins Consisting Of Quarters And Half Dollars
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Consider The Differential Equation Dy Dx Y 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.