Domain Of X 2 X 1
faraar
Sep 20, 2025 · 6 min read
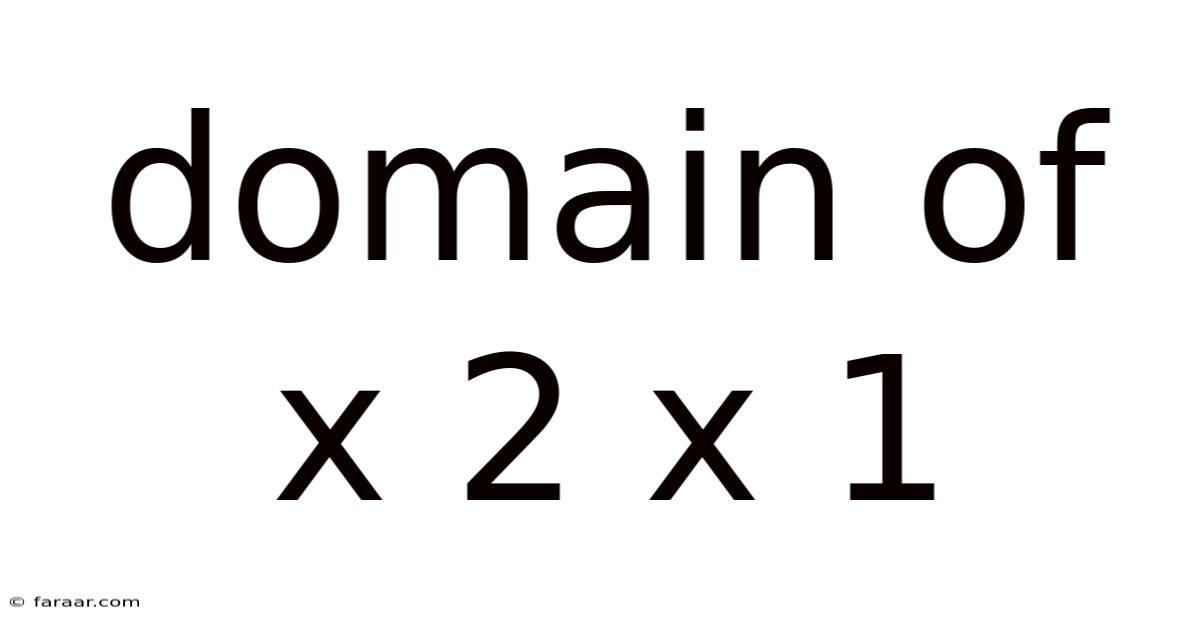
Table of Contents
Unveiling the Mysteries of the Domain of x² - 2x + 1: A Comprehensive Guide
Understanding the domain of a function is a fundamental concept in algebra and calculus. This article delves deep into determining the domain of the function f(x) = x² - 2x + 1, exploring its characteristics, potential restrictions, and implications. We'll break down the process step-by-step, providing a clear and comprehensive guide suitable for students and anyone seeking to strengthen their understanding of functions and their domains. By the end, you'll not only know the domain of this specific function but also possess the tools to analyze the domain of other polynomial and more complex functions.
Introduction: What is a Domain?
Before we dive into the specifics of x² - 2x + 1, let's establish a solid foundation. The domain of a function is the set of all possible input values (x-values) for which the function is defined. In simpler terms, it's the range of x-values that you can "plug into" the function and get a valid, real-number output. Functions can be restricted in their domains due to several factors, including:
- Division by zero: The denominator of a fraction cannot be zero.
- Even roots of negative numbers: You can't take the square root (or any even root) of a negative number and obtain a real number.
- Logarithms of non-positive numbers: The argument of a logarithm must be positive.
Our focus today is on the polynomial function f(x) = x² - 2x + 1. Polynomials are generally well-behaved functions, meaning they are defined for all real numbers unless otherwise restricted. Let’s examine why this is the case and then explore the specific characteristics of our function.
Analyzing the Domain of f(x) = x² - 2x + 1
The function f(x) = x² - 2x + 1 is a quadratic function. Quadratic functions are polynomials of degree 2, meaning the highest power of x is 2. A general form of a quadratic function is ax² + bx + c, where a, b, and c are constants. In our case, a = 1, b = -2, and c = 1.
Why is the domain of a polynomial usually all real numbers?
Polynomials are defined for all real numbers because there are no operations that can lead to undefined results. You can raise any real number to any integer power, and you can multiply and add real numbers together without encountering any restrictions. There are no divisions, square roots, or logarithms involved, eliminating the potential issues mentioned earlier.
Therefore, the domain of f(x) = x² - 2x + 1 is all real numbers. This can be expressed in several ways:
- Interval notation: (-∞, ∞)
- Set-builder notation: {x | x ∈ ℝ} (This reads as "the set of all x such that x is an element of the real numbers")
- In words: All real numbers
Graphical Representation and Intuition
Visualizing the function can further solidify our understanding. The graph of f(x) = x² - 2x + 1 is a parabola that opens upwards. This parabola extends infinitely in both the positive and negative x-directions. This visual representation confirms that there are no x-values for which the function is undefined. Every x-value will produce a corresponding y-value.
Algebraic Manipulation and Factoring
It's often insightful to manipulate the function algebraically. Notice that f(x) = x² - 2x + 1 is a perfect square trinomial. It can be factored as:
f(x) = (x - 1)²
This factored form highlights the function's vertex at (1, 0). The function is a parabola symmetric around x = 1. Even with this factored form, there are no restrictions on the input values; any real number can be squared.
Comparing to Other Functions with Restricted Domains
Let's briefly contrast our function with examples of functions having restricted domains to highlight the unique characteristics of f(x) = x² - 2x + 1:
- g(x) = 1/x: The domain of this function is all real numbers except x = 0 (because division by zero is undefined).
- h(x) = √x: The domain is all non-negative real numbers (x ≥ 0) because we cannot take the square root of a negative number and get a real result.
- i(x) = ln(x): The domain is all positive real numbers (x > 0) because the logarithm of a non-positive number is undefined.
These examples show that the unrestricted domain of f(x) = x² - 2x + 1 is a consequence of its polynomial nature and the absence of operations that could lead to undefined results.
Advanced Concepts and Extensions
While the domain of f(x) = x² - 2x + 1 is straightforward, this understanding serves as a crucial foundation for tackling more complex functions. Let's briefly touch upon some advanced concepts:
- Piecewise functions: Functions defined differently over different intervals. Determining the domain of a piecewise function involves considering the domain of each piece.
- Composite functions: Functions within functions. The domain of a composite function is influenced by the domains of the individual functions.
- Functions with parameters: Functions involving constants that can be varied. Analyzing the domain might require consideration of the parameter's values.
Frequently Asked Questions (FAQ)
Q: Can the range of f(x) = x² - 2x + 1 be determined?
A: Yes, the range of f(x) = x² - 2x + 1 is [0, ∞). Since the parabola opens upwards and has a vertex at (1,0), the minimum value of the function is 0, and it extends infinitely in the positive y-direction.
Q: What about complex numbers? Does the domain extend to complex numbers?
A: If we expand the consideration to the complex numbers, the domain would indeed include all complex numbers. However, our discussion has focused on real-valued functions and their real-valued domains.
Q: How does the domain affect graphing the function?
A: The domain determines the x-values that are included in the graph. Since the domain of f(x) = x² - 2x + 1 is all real numbers, the graph extends infinitely along the x-axis.
Conclusion: Mastering Domains – A Key to Functional Understanding
Understanding the domain of a function is a pivotal skill in mathematics. This comprehensive analysis of f(x) = x² - 2x + 1 has demonstrated that the domain of this quadratic function is all real numbers, a consequence of its polynomial nature. We've explored the underlying reasons for this unrestricted domain and compared it to functions with more limited domains. This foundational knowledge paves the way for tackling more advanced functional concepts and is crucial for success in higher-level mathematics and related fields. The simplicity of this example provides a strong base for understanding the more complex concepts involving domains of rational, radical, and logarithmic functions. Remember, grasping the concept of domain is key to fully understanding and manipulating functions.
Latest Posts
Latest Posts
-
Civil Service Exam Ap World History Definition
Sep 20, 2025
-
When Is A Rhombus A Square
Sep 20, 2025
-
1 Ln N Converge Or Diverge
Sep 20, 2025
-
Graph The Equation Y 2 3x
Sep 20, 2025
-
Can An Obtuse Triangle Be Equilateral
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Domain Of X 2 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.