8x10-3 Is How Many Times As Great As 4x10-6
faraar
Sep 14, 2025 · 5 min read
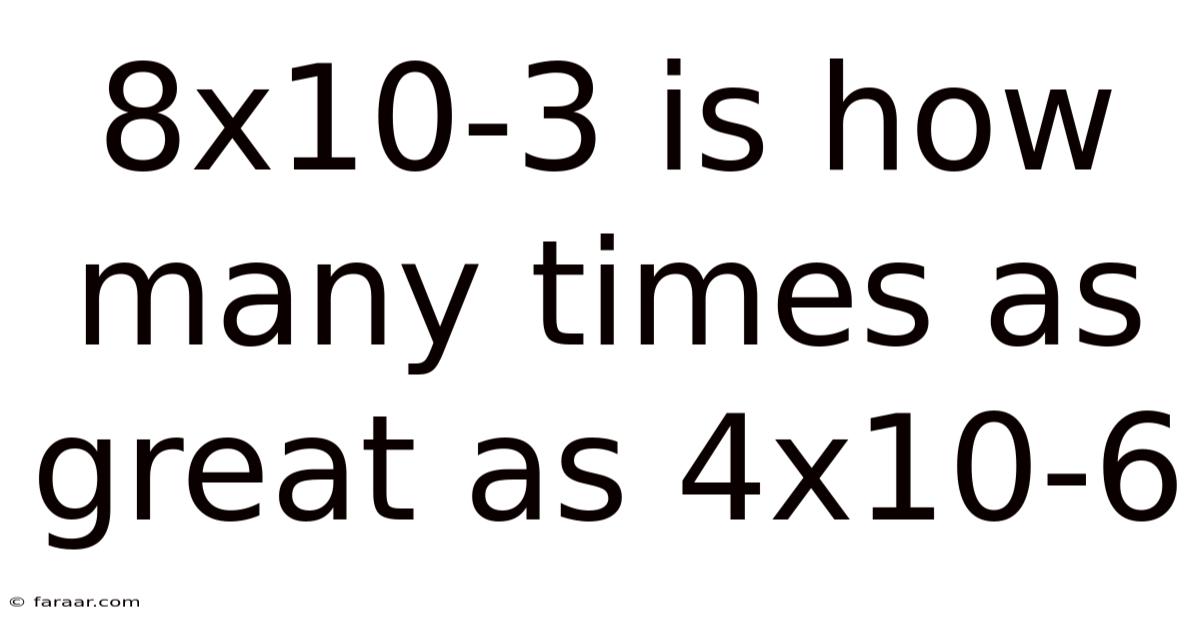
Table of Contents
8 x 10⁻³ is How Many Times as Great as 4 x 10⁻⁶? A Deep Dive into Scientific Notation and Comparative Magnitude
Understanding the relative size of numbers expressed in scientific notation is a fundamental skill in many scientific and mathematical fields. This article will not only answer the question, "8 x 10⁻³ is how many times as great as 4 x 10⁻⁶?", but also provide a comprehensive understanding of the underlying principles and techniques involved. We'll delve into the intricacies of scientific notation, explore different methods for solving this type of problem, and offer a detailed explanation to solidify your understanding. By the end, you'll be equipped to tackle similar comparisons with confidence.
Introduction: Scientific Notation and its Importance
Scientific notation is a standardized way of writing very large or very small numbers. It uses powers of ten to represent the magnitude of a number concisely. A number in scientific notation is expressed in the form a x 10<sup>b</sup>, where a is a number between 1 and 10 (but not including 10), and b is an integer representing the exponent. This method simplifies complex calculations and improves readability, particularly in fields like physics, chemistry, and astronomy where extremely large or small values are commonplace. Mastering scientific notation is crucial for accurately interpreting and comparing numerical data.
Understanding the Problem: 8 x 10⁻³ vs. 4 x 10⁻⁶
Our core problem asks how many times larger 8 x 10⁻³ is than 4 x 10⁻⁶. This involves comparing the magnitudes of two numbers expressed in scientific notation. The key to solving this lies in understanding the relationship between the coefficients (8 and 4) and the exponents (-3 and -6). We need to determine the ratio between these two numbers. Intuitively, we can see that 8 is twice as large as 4, and 10⁻³ is significantly larger than 10⁻⁶. But how do we quantify this difference precisely?
Method 1: Direct Division
The most straightforward method is to divide the larger number (8 x 10⁻³) by the smaller number (4 x 10⁻⁶):
(8 x 10⁻³) / (4 x 10⁻⁶)
We can separate this division into two parts:
(8/4) x (10⁻³/10⁻⁶)
-
8/4 = 2 This is the ratio of the coefficients.
-
10⁻³/10⁻⁶ = 10⁻³⁻⁻⁶ = 10³ = 1000 This is the ratio of the powers of ten. Remember, when dividing exponents with the same base, you subtract the exponents.
Therefore, the final answer is 2 x 1000 = 2000. 8 x 10⁻³ is 2000 times as great as 4 x 10⁻⁶.
Method 2: Converting to Standard Form
An alternative approach involves converting both numbers to standard (decimal) form before comparison.
-
8 x 10⁻³ = 0.008 (Move the decimal point three places to the left)
-
4 x 10⁻⁶ = 0.000004 (Move the decimal point six places to the left)
Now we perform the division:
0.008 / 0.000004 = 2000
This method confirms the result obtained using direct division. While this method is conceptually simpler for those less familiar with exponent rules, it becomes less efficient when dealing with extremely large or small numbers.
Method 3: Adjusting Exponents for Easier Comparison
A more elegant approach involves manipulating the scientific notation to make the exponents equal before comparing the coefficients. We can rewrite 8 x 10⁻³ as follows:
8 x 10⁻³ = 8000 x 10⁻⁶
Notice that we multiplied the coefficient by 1000 (10³) and simultaneously divided the power of ten by 10³ to maintain the equality. Now, we can directly compare the coefficients:
(8000 x 10⁻⁶) / (4 x 10⁻⁶) = 8000/4 = 2000
This method highlights the relative magnitude difference more clearly, emphasizing the 1000-fold difference in the powers of ten.
Scientific Explanation: Order of Magnitude and Significant Figures
The significant difference between 8 x 10⁻³ and 4 x 10⁻⁶ highlights the concept of order of magnitude. The order of magnitude represents the power of ten closest to the number. In this case, 8 x 10⁻³ has an order of magnitude of 10⁻³, while 4 x 10⁻⁶ has an order of magnitude of 10⁻⁶. The three-order-of-magnitude difference directly translates to a factor of 1000 (10³).
Furthermore, it's important to consider significant figures. Both numbers given have only one significant figure (8 and 4). Therefore, our final answer of 2000 should ideally be represented with only one significant figure, which would be 2 x 10³. This illustrates the importance of maintaining appropriate precision in scientific calculations.
Practical Applications: Real-World Examples
Understanding relative magnitudes expressed in scientific notation is vital in various fields:
-
Physics: Comparing the strength of different forces, measuring distances in space, or analyzing the energy levels of particles.
-
Chemistry: Determining the concentration of solutions, calculating reaction rates, or comparing the masses of atoms and molecules.
-
Biology: Measuring the size of cells, analyzing population growth rates, or comparing genetic sequences.
-
Engineering: Designing structures capable of withstanding specific forces, calculating the flow rate of fluids, or assessing the power output of machines.
Frequently Asked Questions (FAQ)
Q: What if the numbers had different bases (e.g., base 2 instead of base 10)?
A: The principles remain the same, but the calculations would involve different logarithmic properties specific to the chosen base. The core concept of comparing coefficients and exponents still applies.
Q: How would this be solved using logarithms?
A: Logarithms can simplify the comparison, particularly for complex numbers. Taking the logarithm of both numbers allows you to directly compare the exponents, and the difference between the logarithms corresponds to the relative magnitude.
Q: Can I use a calculator for this type of problem?
A: Yes, most scientific calculators can handle calculations involving scientific notation directly, simplifying the process. However, understanding the underlying mathematical principles is still crucial.
Conclusion: Mastering Relative Magnitude Comparisons
This detailed analysis shows that 8 x 10⁻³ is 2000 times as great as 4 x 10⁻⁶. We explored three different methods to reach this conclusion, highlighting the versatility of approaches available when dealing with scientific notation. Understanding these techniques is essential for accurately interpreting and manipulating numerical data across various scientific and mathematical disciplines. This skill is not only valuable for problem-solving but also crucial for critical thinking and data analysis. The ability to confidently compare magnitudes expressed in scientific notation is a hallmark of scientific literacy, equipping you to navigate the quantitative world around us with greater clarity and understanding. Remember to always consider significant figures for accuracy in your final answer.
Latest Posts
Latest Posts
-
Which Of The Following Problems Would Not Have A Solution
Sep 14, 2025
-
How To Convert Micromoles To Milligrams
Sep 14, 2025
-
3 N 11 5n 2 N 12 9
Sep 14, 2025
-
Rounding To The Nearest Ten Thousandths
Sep 14, 2025
-
Write A Function Formula For G Using The Function F
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 8x10-3 Is How Many Times As Great As 4x10-6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.