3 N 11 5n 2 N 12 9
faraar
Sep 14, 2025 · 5 min read
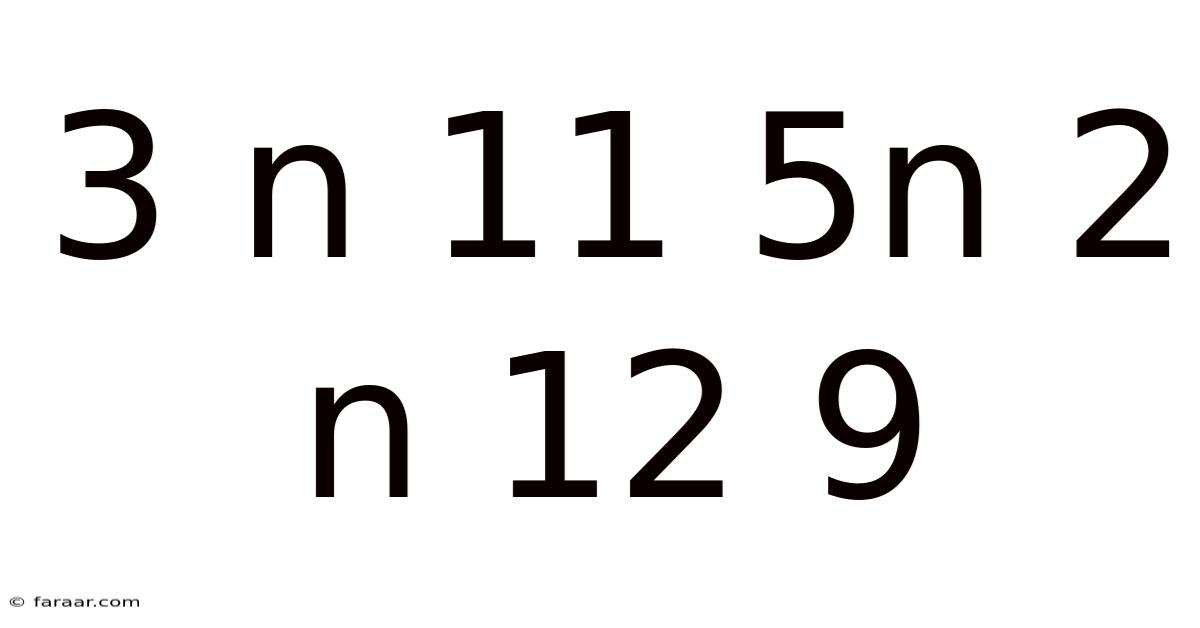
Table of Contents
Decoding the Sequence: Unraveling the Mystery of 3, 11, 5, 2, 12, 9...
This article delves into the fascinating world of number sequences and explores the potential patterns and solutions behind the seemingly random sequence: 3, 11, 5, 2, 12, 9. We'll investigate various mathematical approaches, from simple arithmetic progressions to more complex algorithms, to uncover the underlying logic and potentially predict the next numbers in this intriguing sequence. Understanding number sequences enhances logical reasoning and problem-solving skills, vital tools in various fields, from mathematics and computer science to cryptography and data analysis.
Introduction: The Allure of Number Sequences
Number sequences, whether seemingly random or intricately structured, present a captivating challenge. They demand careful observation, logical deduction, and the application of mathematical principles to unravel their hidden rules. This particular sequence, 3, 11, 5, 2, 12, 9, doesn't immediately reveal a straightforward pattern. However, by systematically exploring different possibilities, we can uncover potential solutions and appreciate the beauty of mathematical logic. This exploration will involve a combination of analytical thinking, pattern recognition, and testing different hypotheses.
Exploring Potential Patterns: A Systematic Approach
Given the lack of an immediately obvious pattern, we'll adopt a systematic approach. This involves considering several possibilities:
-
Arithmetic Progressions: We'll check for constant differences between consecutive numbers. A quick glance reveals that this isn't the case. The differences are not consistent.
-
Geometric Progressions: We'll look for a constant ratio between consecutive terms. Again, a cursory examination shows no such consistent ratio exists.
-
Alternating Sequences: Perhaps the sequence is composed of two intertwined sequences. We can separate the odd-indexed terms (3, 5, 12) and the even-indexed terms (11, 2, 9). Analyzing each subsequence separately might reveal a hidden pattern. Let's explore this further.
Analyzing Subsequences: Uncovering Hidden Patterns
Let's examine the two subsequences derived from the original sequence:
Subsequence 1 (Odd-Indexed Terms): 3, 5, 12
This subsequence doesn't immediately suggest a simple arithmetic or geometric progression. However, let's consider other possibilities:
-
Differences between consecutive terms: 5 - 3 = 2; 12 - 5 = 7. The differences themselves don't form a consistent pattern.
-
Relationship between terms: We could explore if there's a functional relationship between the terms. For instance, is there a formula that generates each term based on its position in the sequence? This requires more complex mathematical investigation.
Subsequence 2 (Even-Indexed Terms): 11, 2, 9
Similar to Subsequence 1, this subsequence also lacks an apparent simple pattern. Let's analyze it:
-
Differences between consecutive terms: 2 - 11 = -9; 9 - 2 = 7. Again, the differences don't form a clear pattern.
-
Relationship between terms: Exploring functional relationships between the terms of this subsequence is also necessary.
Advanced Mathematical Approaches: Exploring Deeper Relationships
Since simple arithmetic and geometric progressions, and even straightforward alternating sequences, fail to explain the pattern, we need to explore more advanced mathematical techniques. These include:
-
Polynomial Interpolation: We could attempt to fit a polynomial function to the data points. This involves finding a polynomial equation whose values match the given sequence at specific points. However, for a sequence of only six terms, the resulting polynomial might be complex and not necessarily predictive of future terms.
-
Recursive Relationships: A recursive relationship defines each term in the sequence based on previous terms. This is a common approach in solving more intricate number sequences. We could explore if there's a formula that describes each term as a function of one or more preceding terms.
-
Modular Arithmetic: Could there be a pattern if we consider the remainders when the terms are divided by a specific number? This requires experimenting with different moduli to see if any patterns emerge.
The Importance of Context and Further Information
The lack of a clear, readily identifiable pattern emphasizes the importance of context when dealing with number sequences. Without additional information or constraints, it's challenging to definitively determine the underlying rule. It's possible that:
-
The sequence is incomplete: The six given numbers may only be a fragment of a larger, more complex sequence.
-
The sequence is arbitrary: It might have been designed without a consistent mathematical rule, perhaps for a puzzle or code.
-
The sequence is based on a hidden, more complex algorithm: The rule governing the sequence might be based on a sophisticated mathematical concept that's not immediately obvious.
-
The sequence is based on external factors: The numbers could represent coded information or relate to some external system not immediately apparent from the numbers themselves.
Conclusion: The Ongoing Search for Patterns
Unraveling the mystery of the sequence 3, 11, 5, 2, 12, 9 requires a systematic and persistent approach. While simple arithmetic and geometric progressions are not directly applicable, exploring more advanced mathematical tools, such as polynomial interpolation, recursive relationships, and modular arithmetic, could lead to potential solutions. However, the absence of a clearly identifiable pattern highlights the importance of considering the context and the possibility of incomplete information or more complex underlying principles. The exploration itself underscores the value of logical reasoning, problem-solving, and the enduring fascination with mathematical puzzles. Further research and analysis, possibly with more data points, are needed to definitively determine the governing rule of this intriguing number sequence.
Further Explorations and Challenges
To further challenge yourself and deepen your understanding of number sequences, consider these questions:
-
Generating Your Own Sequence: Try creating your own number sequences based on various rules. Then, challenge a friend or colleague to decipher your sequence.
-
Exploring Online Resources: Numerous online resources and databases of number sequences exist. Exploring these resources can expose you to a wider variety of sequence types and their underlying rules.
-
Delving into Number Theory: Studying number theory, a branch of mathematics concerned with the properties of numbers, can greatly enhance your ability to analyze and understand complex number sequences.
By continuously engaging with these challenges, you'll refine your analytical skills and cultivate a deeper appreciation for the beauty and complexity hidden within seemingly simple number patterns. The journey of exploring number sequences is a testament to the power of logical thinking and mathematical exploration.
Latest Posts
Latest Posts
-
2x Y 4 Solve For Y
Sep 15, 2025
-
What Is 1 2 To The Power Of 3
Sep 15, 2025
-
What Is Half Of 5 8 In A Fraction
Sep 15, 2025
-
Average Rate Of Change Vs Instantaneous Rate Of Change
Sep 15, 2025
-
How Much Is 3 4 Lb
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3 N 11 5n 2 N 12 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.