84 Is 75 Of What Number
faraar
Sep 20, 2025 · 5 min read
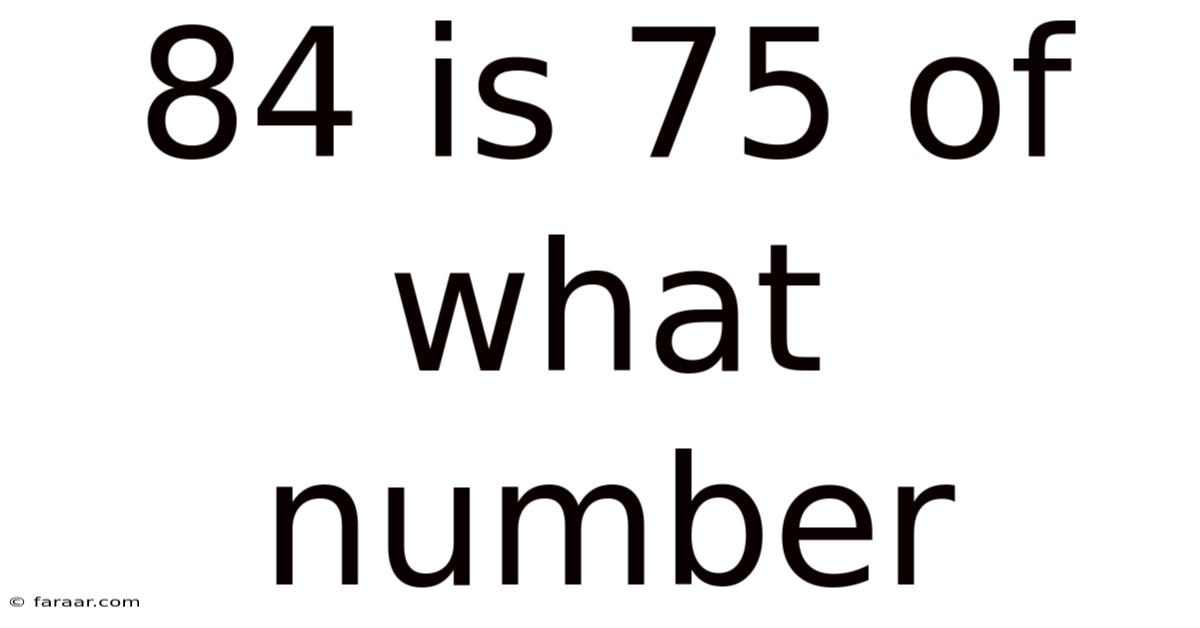
Table of Contents
Solving the Percentage Problem: 84 is 75% of What Number?
Finding an unknown value based on a percentage is a common problem in mathematics, with applications spanning various fields like finance, science, and everyday life. This article will comprehensively explore how to solve the problem: "84 is 75% of what number?" We'll delve into different methods, explain the underlying concepts, and provide practical examples to solidify your understanding. This guide is perfect for students, professionals, or anyone wanting to improve their percentage calculation skills. By the end, you'll not only understand how to solve this specific problem but also master the techniques to tackle similar percentage questions.
Understanding Percentage Problems
Before diving into the solution, let's clarify the core concept. Percentage problems generally involve three components:
- The Part: This represents a portion of a whole. In our problem, "84" is the part.
- The Percentage: This indicates the fraction of the whole that the part represents. Here, it's "75%".
- The Whole: This is the total value from which the part is derived. This is the unknown value we need to find.
Our problem can be expressed as: 84 = 75% * x (where x is the unknown whole number).
Method 1: Using the Equation
The most straightforward approach is to translate the problem into an algebraic equation and solve for the unknown variable.
Steps:
-
Write the equation: We can write the problem as: 84 = 0.75 * x (Remember, 75% is equivalent to 0.75 as a decimal).
-
Isolate the variable: To find 'x', we need to isolate it on one side of the equation. We can achieve this by dividing both sides by 0.75:
x = 84 / 0.75
-
Calculate the result: Performing the division gives us:
x = 112
Therefore, 84 is 75% of 112.
Method 2: Using Proportions
Proportions offer a visual and intuitive way to solve percentage problems. We can set up a proportion by relating the part to the whole and the percentage to 100%.
Steps:
-
Set up the proportion: We can express the problem as a proportion:
84/x = 75/100
-
Cross-multiply: Cross-multiplying the terms gives us:
84 * 100 = 75 * x
-
Solve for x: This simplifies to:
8400 = 75x
x = 8400 / 75
-
Calculate the result: Performing the division yields:
x = 112
Again, we find that 84 is 75% of 112.
Method 3: Using the Percentage Formula
The percentage formula provides a direct method for calculating the whole given the part and the percentage.
Steps:
-
Recall the formula: The general percentage formula is:
(Part / Whole) * 100% = Percentage
-
Substitute the known values: Plugging in the values from our problem, we have:
(84 / x) * 100% = 75%
-
Solve for x: First, divide both sides by 100%:
84 / x = 0.75
-
Isolate x: Now, multiply both sides by x and divide both sides by 0.75:
x = 84 / 0.75
-
Calculate the result: The calculation gives us:
x = 112
This reaffirms that 84 is 75% of 112.
Method 4: Working with Fractions
Percentages can be expressed as fractions. This method uses this representation to solve the problem.
Steps:
-
Convert the percentage to a fraction: 75% is equivalent to 75/100, which simplifies to 3/4.
-
Set up an equation: We can write the equation as:
84 = (3/4) * x
-
Solve for x: Multiply both sides by 4/3 (the reciprocal of 3/4):
x = 84 * (4/3)
-
Calculate the result: This simplifies to:
x = 28 * 4 = 112
Hence, 84 is 75% of 112.
Illustrative Examples
Let's apply these methods to a few more examples to build your confidence and understanding.
Example 1: 60 is 20% of what number?
Using the equation method: 60 = 0.20 * x => x = 60 / 0.20 = 300
Example 2: 150 is 75% of what number?
Using the proportion method: 150/x = 75/100 => 15000 = 75x => x = 15000/75 = 200
Example 3: 25 is 5% of what number?
Using the fractional method: 25 = (5/100) * x => 25 = (1/20) * x => x = 25 * 20 = 500
Common Mistakes to Avoid
When solving percentage problems, be mindful of these common mistakes:
- Incorrect Decimal Conversion: Ensure you accurately convert percentages to decimals (e.g., 75% = 0.75). A small error here can significantly impact the final result.
- Arithmetic Errors: Double-check your calculations to minimize errors in addition, subtraction, multiplication, and division.
- Mixing Up Part and Whole: Carefully identify the part and the whole in the problem statement to avoid substituting them incorrectly in the equation or proportion.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator for these problems?
A1: Absolutely! Calculators are particularly helpful when dealing with more complex decimal calculations. However, understanding the underlying methods is crucial, even when using a calculator.
Q2: What if the percentage is greater than 100%?
A2: If the percentage is greater than 100%, the unknown number (the whole) will be smaller than the given part. The methods described above still apply; you just need to be aware that your answer will be less than the given part.
Q3: Are there other methods to solve percentage problems?
A3: Yes, there are other, more advanced techniques, especially when dealing with more complex scenarios involving multiple percentages or compounded interest. These often involve logarithmic or exponential functions. However, the methods discussed here provide a solid foundation for solving most common percentage problems.
Conclusion
Solving percentage problems, like determining what number 84 represents 75% of, requires a clear understanding of the concepts and the ability to apply appropriate methods. We have explored four different approaches—using equations, proportions, the percentage formula, and fractions—each offering a slightly different perspective on the same problem. By mastering these methods, you'll not only confidently solve this specific problem but also develop the skills to tackle a wide range of percentage calculations effectively and efficiently. Remember to practice regularly to build your proficiency and identify the method that best suits your individual learning style. The key is to understand the underlying principles rather than just memorizing formulas.
Latest Posts
Latest Posts
-
Can An Obtuse Triangle Be Equilateral
Sep 20, 2025
-
How To Find Maximum Number Of Real Zeros
Sep 20, 2025
-
What Is 10 More Than 15
Sep 20, 2025
-
What Happened To The Third Atomic Bomb
Sep 20, 2025
-
Bacl2 Na2co3 Net Ionic Equation
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 84 Is 75 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.