7 Less Than 4 Times A Number
faraar
Sep 09, 2025 · 6 min read
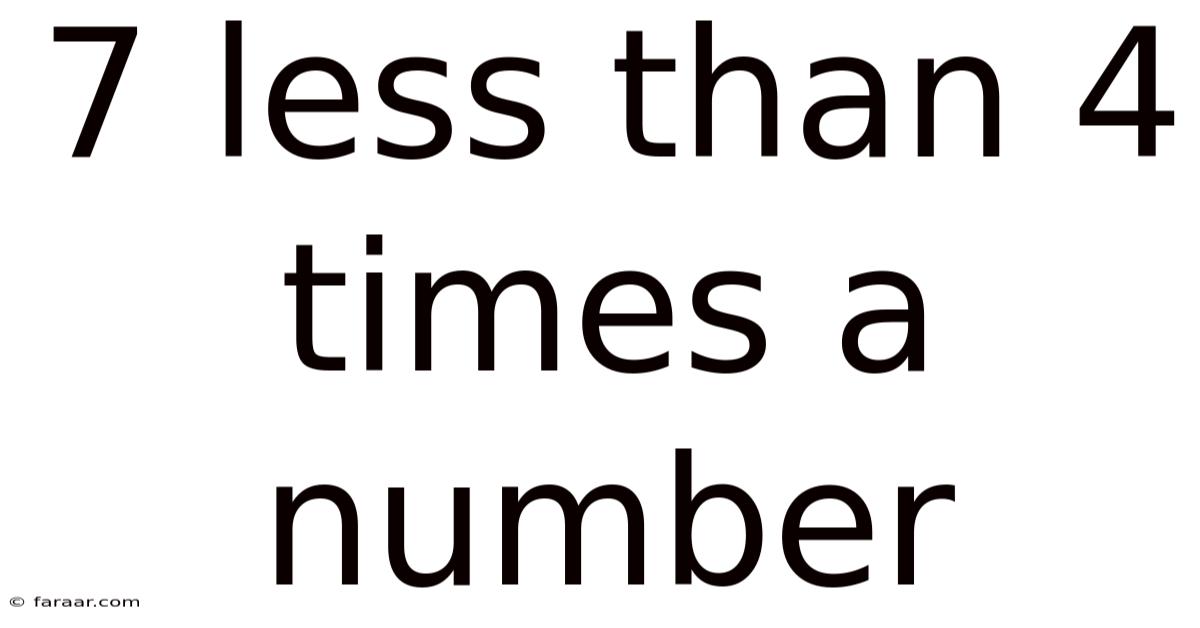
Table of Contents
Decoding "7 Less Than 4 Times a Number": A Deep Dive into Algebraic Expressions
This article explores the seemingly simple phrase "7 less than 4 times a number," unraveling its mathematical meaning and demonstrating its application in various problem-solving scenarios. We'll delve into the process of translating this phrase into an algebraic expression, solving equations derived from it, and understanding its implications in real-world contexts. This will equip you with the skills to confidently tackle similar problems involving algebraic expressions and equations. We’ll also cover frequently asked questions and offer insightful examples to reinforce your understanding.
Introduction: Understanding the Language of Math
Mathematics is a language, and like any language, it requires understanding its grammar and vocabulary. The phrase "7 less than 4 times a number" is a concise mathematical statement that needs to be translated into symbolic form—an algebraic expression. This seemingly simple phrase encapsulates a crucial concept in algebra: the ability to represent real-world situations using mathematical notation. Mastering this skill is fundamental to solving a wide range of problems.
Step-by-Step Translation into an Algebraic Expression
Let's break down the phrase step-by-step:
-
"A number": This represents an unknown value, which we conventionally represent with a variable, typically 'x'.
-
"4 times a number": This translates to 4 multiplied by 'x', or 4x.
-
"7 less than 4 times a number": This signifies subtracting 7 from the result of 4x. Therefore, the complete algebraic expression becomes 4x - 7.
This simple expression now allows us to perform various mathematical operations and solve problems.
Illustrative Examples: Putting the Expression to Work
Let's consider a few examples demonstrating the practical application of the expression 4x - 7:
Example 1: Finding the Number
Problem: "7 less than 4 times a number is 17. Find the number."
Solution: We can translate this problem directly into an equation:
4x - 7 = 17
To solve for x, we follow these steps:
- Add 7 to both sides: 4x = 24
- Divide both sides by 4: x = 6
Therefore, the number is 6.
Example 2: Word Problem Application
Problem: Sarah is four times as old as her son, Michael. Seven years ago, Sarah was seventeen years older than Michael. How old is Michael now?
Solution: Let's represent Michael's current age as 'x'. Sarah's current age is then 4x. Seven years ago, Michael's age was (x - 7) and Sarah's age was (4x - 7). The problem states that seven years ago, Sarah was seventeen years older than Michael:
(4x - 7) = (x - 7) + 17
Simplifying the equation:
4x - 7 = x + 10 3x = 17 x = 17/3
This result (17/3) is not a whole number, which may indicate an error in the problem statement. Let’s adjust the problem slightly to make it solvable with a whole number result. Let’s say Sarah was 17 years older than Michael today, not 7 years ago.
Then the equation becomes:
4x = x + 17 3x = 17 x ≈ 5.67
Again, not a whole number, suggesting that the original problem likely needs adjustment.
Let's revise the problem statement to be more realistic. Suppose seven years ago, Sarah was 17 years older than Michael. This gives us:
4x - 7 = x -7 + 17
Solving for x:
3x = 17 x = 17/3
This still doesn't provide a whole number result for x. Let's try a different approach, and instead state that the difference in their ages remains constant:
4x - x = 17 3x = 17 x = 17/3
This continues to highlight the importance of accurately defining the problem statement and ensuring internal consistency. The original question needed clearer formulation for a solvable outcome with whole numbers.
Example 3: Geometric Application
Problem: The length of a rectangle is 7 units less than 4 times its width. If the length is 17 units, what is the width?
Solution: Let's denote the width as 'x'. The length is then expressed as 4x - 7. We are given that the length is 17 units. Thus:
4x - 7 = 17 4x = 24 x = 6
The width of the rectangle is 6 units.
Advanced Concepts: Expanding the Scope
The simple expression 4x - 7 can serve as a foundation for exploring more complex algebraic concepts:
-
Inequalities: Instead of an equation, we could have an inequality, such as 4x - 7 > 10. Solving this would involve similar steps, but the result would be a range of values for 'x' rather than a single solution.
-
Quadratic Equations: We might encounter a scenario where the expression 4x - 7 is part of a quadratic equation, necessitating more advanced solving techniques.
-
Functions: The expression could represent a function, f(x) = 4x - 7, where different inputs (x) yield different outputs (f(x)). Graphing this function would reveal a straight line with a slope of 4 and a y-intercept of -7.
Understanding the Scientific Basis: Linear Equations
The algebraic expression 4x - 7 represents a linear equation. Linear equations are fundamental in mathematics and have a wide range of applications in various fields. They describe relationships between variables that result in a straight-line graph. The equation's slope (4 in this case) indicates the rate of change, and the y-intercept (-7) is the value of the dependent variable when the independent variable is zero.
Frequently Asked Questions (FAQs)
-
Q: What if the phrase was "7 less than 4 times a number is equal to zero"? How would I solve that?
A: The equation would be 4x - 7 = 0. Solving this: 4x = 7; x = 7/4 or 1.75*
-
Q: Can I use a different variable instead of 'x'?
A: Absolutely! Any letter or symbol can represent the unknown number. 'y', 'n', or even a Greek letter like 'α' would work equally well. The choice is largely a matter of convention and personal preference.*
-
Q: What are some real-world applications beyond the examples provided?
A: This type of algebraic expression finds applications in various fields, including physics (calculating distances or velocities), engineering (modeling systems), finance (calculating profits or losses), and even everyday situations like budgeting or recipe scaling.*
Conclusion: Mastering Algebraic Expressions – A Stepping Stone to Success
Understanding how to translate phrases like "7 less than 4 times a number" into algebraic expressions is a crucial skill in mathematics. It forms the basis for solving a wide range of problems and opens the door to more advanced mathematical concepts. By mastering this fundamental skill, you'll build a solid foundation for success in algebra and beyond. Remember to practice regularly, and don't hesitate to explore different problem scenarios to solidify your understanding. The ability to translate word problems into mathematical equations is a powerful tool, allowing you to approach complex challenges with clarity and precision.
Latest Posts
Latest Posts
-
Vertical Shrink By A Factor Of 1 3
Sep 09, 2025
-
How Many Words Should Your College Essay Be
Sep 09, 2025
-
What Is The Charge Of Chromium
Sep 09, 2025
-
2 1 3 1 3 4
Sep 09, 2025
-
Express Y In Terms Of X
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 7 Less Than 4 Times A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.