7 9 Divided By 1 3
faraar
Sep 23, 2025 · 6 min read
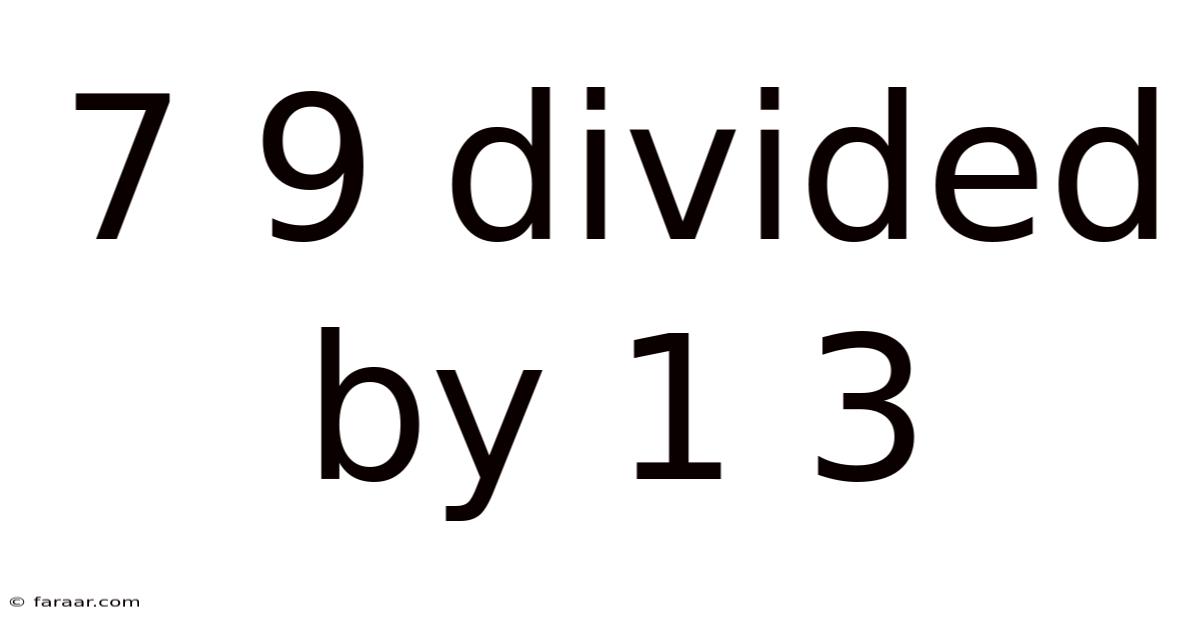
Table of Contents
Decoding Division: A Deep Dive into 7/9 ÷ 1/3
This article will explore the seemingly simple yet often misunderstood mathematical operation: dividing fractions, specifically 7/9 divided by 1/3. We'll move beyond just finding the answer and delve into the underlying principles, offering a comprehensive understanding that goes beyond rote memorization. This detailed explanation will cover the process step-by-step, provide the scientific rationale behind the method, address frequently asked questions, and ultimately empower you with a solid grasp of fraction division.
Introduction: Why Fractions Matter
Fractions are fundamental building blocks of mathematics. Understanding fraction division is crucial not just for passing math tests but for real-world applications ranging from cooking and construction to advanced scientific calculations. This seemingly simple problem, 7/9 ÷ 1/3, encapsulates the core concepts needed to master fraction division, making it an excellent case study. We will build our understanding from the basics, ensuring that even those who struggle with fractions can confidently solve this and similar problems.
Understanding the Basics: What Does Division Mean?
Before tackling fraction division, let's revisit the concept of division itself. When we divide a number (the dividend) by another number (the divisor), we are essentially asking: "How many times does the divisor fit into the dividend?" For example, 12 ÷ 3 = 4 because the number 3 fits into 12 four times.
This same principle applies to fractions. 7/9 ÷ 1/3 asks: "How many times does 1/3 fit into 7/9?" This question might seem more abstract, but the underlying concept remains the same.
Method 1: The "Keep, Change, Flip" Method
This is the most common and arguably the easiest method for dividing fractions. It's a shortcut that works reliably every time:
- Keep: Keep the first fraction (the dividend) exactly as it is: 7/9.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (the divisor) – this means inverting the numerator and denominator. 1/3 becomes 3/1.
So, 7/9 ÷ 1/3 becomes 7/9 × 3/1.
-
Multiply: Now, multiply the numerators together and the denominators together: (7 × 3) / (9 × 1) = 21/9.
-
Simplify: Finally, simplify the resulting fraction by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 21 and 9 is 3. Divide both the numerator and denominator by 3: 21/9 = 7/3.
Therefore, 7/9 ÷ 1/3 = 7/3. This can also be expressed as a mixed number: 2 1/3.
Method 2: Finding a Common Denominator
While the "Keep, Change, Flip" method is efficient, understanding the underlying principles is crucial. This method uses a common denominator to illustrate the concept of division more directly.
-
Find a common denominator: Find a common denominator for both fractions. The least common multiple (LCM) of 9 and 3 is 9.
-
Rewrite the fractions: Rewrite both fractions with the common denominator: 7/9 and 3/9 (since 1/3 = 3/9).
-
Divide the numerators: Now, divide the numerator of the first fraction (7) by the numerator of the second fraction (3): 7 ÷ 3 = 7/3.
This method demonstrates that we're essentially comparing the numerators after ensuring they represent the same fractional "unit." The result, 7/3, is the same as the result obtained using the "Keep, Change, Flip" method.
The Scientific Rationale: Why Does "Keep, Change, Flip" Work?
The "Keep, Change, Flip" method is a shortcut derived from the more formal process of dividing fractions. To understand why it works, let's explore the concept of reciprocal.
The reciprocal of a fraction is obtained by swapping the numerator and the denominator. For example, the reciprocal of 1/3 is 3/1 (or simply 3). Multiplying a number by its reciprocal always results in 1.
Dividing by a fraction is equivalent to multiplying by its reciprocal. This is the mathematical foundation of the "Keep, Change, Flip" method. When we change the division sign to multiplication and flip the second fraction, we are essentially multiplying by the reciprocal of the divisor.
Addressing Common Misconceptions
Several common misconceptions surround fraction division:
- Incorrectly flipping the first fraction: Remember, only the second fraction (the divisor) is flipped.
- Forgetting to simplify: Always simplify your answer to its lowest terms.
- Confusing multiplication and division: Division of fractions is distinct from multiplication, although the "Keep, Change, Flip" method utilizes multiplication as part of the process.
Frequently Asked Questions (FAQ)
-
Q: Can I divide fractions with different denominators directly? A: No, you need to either find a common denominator or use the "Keep, Change, Flip" method.
-
Q: What if the divisor is a whole number? A: A whole number can be expressed as a fraction with a denominator of 1. For example, 5 can be expressed as 5/1. Then, you can apply the "Keep, Change, Flip" method as usual.
-
Q: What if I get a fraction as an answer that is an improper fraction? A: It's perfectly acceptable to leave your answer as an improper fraction (where the numerator is larger than the denominator), but you can also convert it to a mixed number if preferred.
-
Q: Why is the "Keep, Change, Flip" method so efficient? A: This method simplifies the process by directly converting division to multiplication, which is generally easier to perform. It leverages the properties of reciprocals to streamline the calculation.
Real-World Applications:
Understanding fraction division isn't just about abstract math; it has numerous real-world applications. For example:
-
Cooking: Scaling recipes up or down requires dividing fractions. If a recipe calls for 1/2 cup of flour and you want to make only 1/3 of the recipe, you need to calculate (1/2) ÷ 3 = 1/6.
-
Sewing/Tailoring: Calculating fabric requirements and adjustments often involve fractional measurements and divisions.
-
Construction: Precise measurements and calculations in construction frequently require working with fractions and their divisions.
-
Engineering: Many engineering calculations rely on accurate fraction manipulation, including division.
Conclusion: Mastering Fraction Division
Mastering fraction division empowers you with a crucial skill applicable in various aspects of life. This article aimed to move beyond simple instruction and provide a comprehensive understanding of the underlying principles. By understanding the "Keep, Change, Flip" method and the rationale behind it, as well as alternative methods, you can approach fraction division with confidence and apply this essential skill across numerous contexts. Remember that practice is key! The more you work with fractions, the more intuitive this process will become. Don't be afraid to tackle more complex fraction division problems to solidify your understanding. The ability to effortlessly work with fractions is a valuable asset for success in mathematics and beyond.
Latest Posts
Latest Posts
-
Handwriting Classes For Adults Near Me
Sep 23, 2025
-
Cos 4x Sin 4x Cos 2x
Sep 23, 2025
-
Line A Is Parallel To Line B
Sep 23, 2025
-
Find The Slope Of A Line Perpendicular
Sep 23, 2025
-
What Is The Measure Of Angle Dfe
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 7 9 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.