64 32 16 8 4 2 1
faraar
Sep 14, 2025 · 5 min read
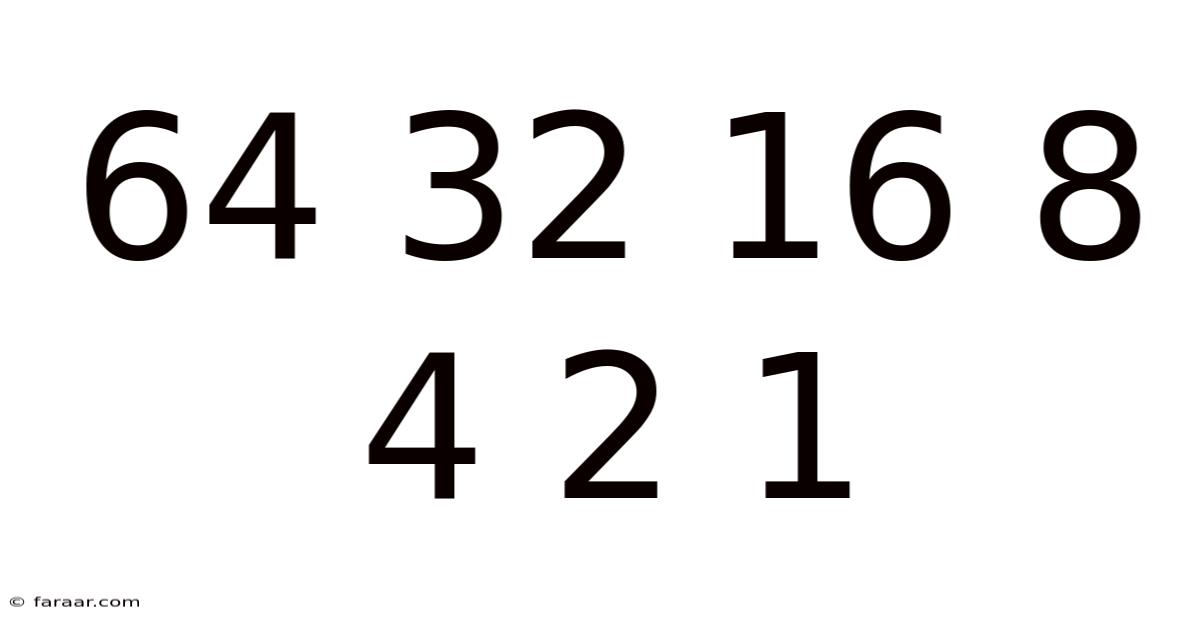
Table of Contents
Decoding the Mystery: Exploring the Sequence 64, 32, 16, 8, 4, 2, 1
The sequence 64, 32, 16, 8, 4, 2, 1 might seem simple at first glance. However, this seemingly straightforward numerical progression hides a wealth of mathematical concepts, practical applications, and fascinating connections to various fields. This article delves deep into this sequence, exploring its underlying patterns, revealing its significance in different contexts, and addressing frequently asked questions. Understanding this sequence unlocks a deeper appreciation for fundamental mathematical principles and their real-world relevance.
Introduction: Recognizing the Pattern
At its core, the sequence 64, 32, 16, 8, 4, 2, 1 represents a geometric progression. This means each subsequent number is obtained by multiplying the preceding number by a constant value – in this case, 1/2 or 0.5. This consistent halving is the key to understanding the sequence's properties and its broader implications. The sequence can also be viewed as successive powers of two, decreasing from 2<sup>6</sup> to 2<sup>0</sup>. This dual perspective – geometric progression and powers of two – is crucial to grasping the full scope of its significance.
Understanding the Geometric Progression
A geometric progression is a sequence where each term is the product of the previous term and a constant value, known as the common ratio. In our sequence, the common ratio is 0.5. Understanding geometric progressions is vital in many areas, including:
- Finance: Calculating compound interest, loan repayments, and investment growth often involves geometric progressions.
- Physics: Modeling exponential decay, such as radioactive decay or the cooling of an object, utilizes geometric progressions.
- Computer Science: Analyzing algorithms and data structures frequently involves geometric progressions, particularly in scenarios involving binary trees or recursive functions.
The Significance of Powers of Two
The sequence 64, 32, 16, 8, 4, 2, 1 can also be expressed as powers of two: 2<sup>6</sup>, 2<sup>5</sup>, 2<sup>4</sup>, 2<sup>3</sup>, 2<sup>2</sup>, 2<sup>1</sup>, 2<sup>0</sup>. This representation highlights the fundamental role of the number two in binary systems, a cornerstone of modern computing.
- Binary System: The binary system, utilizing only 0 and 1, forms the basis of all digital computers. Understanding powers of two is essential for comprehending how computers store and process information. Each bit (binary digit) represents a power of two, allowing for the representation of increasingly larger numbers.
- Data Storage: Data storage units like bytes (8 bits), kilobytes (1024 bytes), megabytes (1024 kilobytes), and so on, all rely on powers of two. The sequence reflects this hierarchical structure of data storage.
- Memory Addressing: In computer memory, addresses are often assigned using powers of two, enabling efficient access to data.
Applications in Real-World Scenarios
The sequence's simple structure belies its widespread practical applications:
- Measurement Conversions: The sequence can be used to illustrate metric conversions, particularly those involving units based on powers of ten. While not a direct correspondence, the principle of halving or doubling is analogous to converting between metric prefixes like kilo, mega, and giga.
- Game Design: Many games utilize level progression or resource allocation based on geometric progressions, providing a balanced and challenging gameplay experience. The increasing difficulty often mirrors the exponential increase of the numbers in the sequence.
- Scientific Modeling: Exponential growth and decay processes in various fields, such as population dynamics, chemical reactions, and epidemiology, can be modeled using geometric progressions similar to this sequence.
Beyond the Sequence: Exploring Related Concepts
The sequence 64, 32, 16, 8, 4, 2, 1 provides a gateway to exploring several key mathematical and computational concepts:
- Exponential Functions: The sequence is a discrete representation of an exponential decay function. Understanding exponential functions is crucial for modeling a wide variety of real-world phenomena.
- Logarithms: Logarithms are the inverse of exponential functions. They are used to solve equations involving exponential terms and are fundamental in various scientific and engineering applications.
- Binary Trees: In computer science, binary trees are hierarchical data structures where each node has at most two children. The number of nodes at each level of a balanced binary tree often follows a geometric progression similar to the sequence.
Frequently Asked Questions (FAQ)
Q: What is the next number in the sequence if it continued?
A: Following the pattern of halving, the next number would be 1/2 or 0.5. The sequence could continue indefinitely, approaching zero asymptotically.
Q: What is the sum of the numbers in the sequence?
A: The sum of the sequence 64, 32, 16, 8, 4, 2, 1 is 127. This is one less than 128 (2<sup>7</sup>), a pattern that holds true for similar geometric progressions based on powers of two.
Q: Are there other sequences with similar properties?
A: Yes, many sequences exhibit similar properties, such as sequences based on other powers (e.g., powers of 3, powers of 10) or sequences with different common ratios in geometric progressions.
Q: How is this sequence used in programming?
A: This sequence directly relates to bit manipulation, memory allocation, and the representation of numbers in binary format within computer programs. Understanding this sequence is crucial for efficient memory management and algorithm design in low-level programming.
Conclusion: The Enduring Relevance of Simple Sequences
The seemingly simple sequence 64, 32, 16, 8, 4, 2, 1 reveals a surprising depth and interconnectedness with various mathematical, computational, and real-world applications. By understanding its underlying principles—geometric progression and powers of two—we gain valuable insights into fundamental concepts that underpin many aspects of our technological world and beyond. This sequence serves as a potent reminder that even the most basic patterns can unlock a deeper appreciation for the beauty and practical relevance of mathematics. Further exploration of related topics, such as exponential functions, logarithms, and binary systems, will solidify this understanding and reveal even more fascinating connections within the realm of mathematics and computer science. The seemingly simple sequence provides a compelling foundation for a journey into deeper mathematical and computational understanding.
Latest Posts
Latest Posts
-
Which Expression Is Equivalent To 8x 12y 32
Sep 14, 2025
-
Slope Intercept Form Vs Point Slope Form
Sep 14, 2025
-
Line Of Action Of The Force
Sep 14, 2025
-
Greatest Common Factor Of 4 And 16
Sep 14, 2025
-
Find The Degree Measure Of Each Angle
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 64 32 16 8 4 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.