Which Expression Is Equivalent To 8x-12y+32
faraar
Sep 14, 2025 · 7 min read
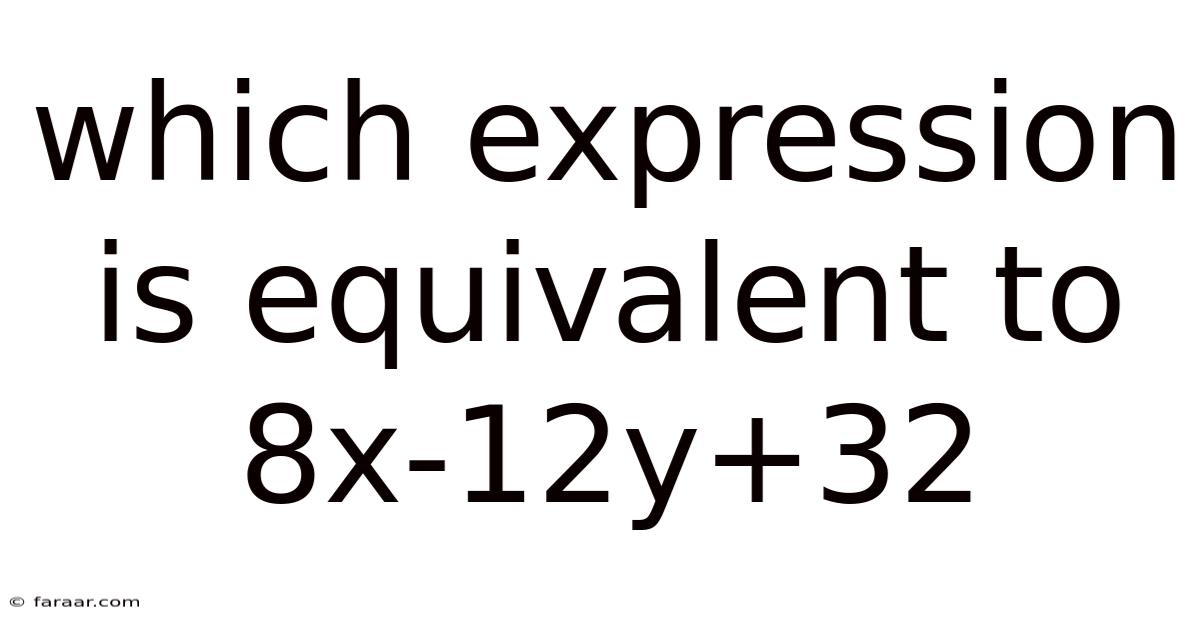
Table of Contents
Unveiling the Equivalents of 8x - 12y + 32: A Deep Dive into Algebraic Expressions
Finding equivalent expressions is a fundamental skill in algebra. This seemingly simple task – identifying expressions that represent the same value regardless of the variable values – underpins a vast amount of mathematical reasoning and problem-solving. This article will explore various methods to find expressions equivalent to 8x - 12y + 32, demonstrating the underlying principles and offering a comprehensive understanding of algebraic manipulation. We'll delve into factoring, expanding, and the crucial concept of maintaining mathematical equality. Understanding these techniques will build a strong foundation for more advanced algebraic concepts.
Understanding Equivalent Expressions
Before we embark on finding equivalent expressions for 8x - 12y + 32, let's define what makes two expressions equivalent. Two algebraic expressions are considered equivalent if they produce the same result for all possible values of the variables involved. This means that no matter what numbers you substitute for 'x' and 'y', the equivalent expressions will always yield identical outcomes. This equivalence is maintained through the application of various algebraic rules and properties, such as the commutative, associative, and distributive properties.
Method 1: Factoring out the Greatest Common Factor (GCF)
One of the most common methods for simplifying and finding equivalent expressions is factoring. This involves identifying the greatest common factor (GCF) among the terms in the expression and then factoring it out. In our expression, 8x - 12y + 32, let's find the GCF of the coefficients 8, -12, and 32.
The factors of 8 are 1, 2, 4, and 8. The factors of -12 are -1, -2, -3, -4, -6, -12, 1, 2, 3, 4, 6, and 12. The factors of 32 are 1, 2, 4, 8, 16, and 32.
The greatest common factor among these three numbers is 4. Therefore, we can factor out 4 from the expression:
4(2x - 3y + 8)
This expression, 4(2x - 3y + 8), is equivalent to 8x - 12y + 32. To verify, we can expand it using the distributive property: 4 * 2x + 4 * (-3y) + 4 * 8 = 8x - 12y + 32. This confirms the equivalence.
Method 2: Rearranging Terms (Commutative Property)
The commutative property of addition states that the order of terms in an addition expression doesn't affect the sum. This means we can rearrange the terms in our expression without changing its value. For instance, we could rewrite 8x - 12y + 32 as:
-12y + 8x + 32 or 32 + 8x - 12y or 32 - 12y + 8x
All these expressions are equivalent to the original expression because the order of addition doesn't alter the final result. This might seem trivial, but understanding the commutative property is crucial for manipulating and simplifying more complex algebraic expressions.
Method 3: Introducing Zero (Additive Identity)
The additive identity property states that adding zero to any expression does not change its value. While this might seem obvious, we can use this property cleverly to create equivalent expressions. We can add and subtract the same term to create an equivalent but different-looking expression. For example:
8x - 12y + 32 + 10 - 10
This expression is still equivalent to the original because we've essentially added zero (10 - 10 = 0). This technique is less commonly used for straightforward simplification, but it becomes more valuable when dealing with more intricate algebraic manipulations, particularly in solving equations.
Method 4: Using the Distributive Property in Reverse (Factoring)
We already used the distributive property in Method 1 to expand the factored expression. The reverse of this process is also a powerful method to find equivalent expressions. Consider the expression:
8(x - 1.5y + 4)
This might not seem immediately equivalent, but applying the distributive property reveals the equivalence:
8 * x - 8 * 1.5y + 8 * 4 = 8x - 12y + 32
This demonstrates that seemingly different expressions can be equivalent depending on how the distributive property is applied. The key is recognizing patterns and common factors that can be factored out or distributed to reveal equivalent forms.
Method 5: Combining like terms (if applicable)
This method applies when dealing with expressions that contain like terms. Like terms are terms that have the same variables raised to the same powers. Our expression 8x - 12y + 32 does not contain like terms; 'x', 'y', and the constant term are all distinct. Therefore, this method is not applicable to the original expression as given. However, let’s consider a slightly different expression to illustrate the principle. For example:
8x + 5y - 2x + 3y + 32
In this expression, 8x and -2x are like terms, as are 5y and 3y. Combining these like terms results in:
(8x - 2x) + (5y + 3y) + 32 = 6x + 8y + 32
This simplified expression is equivalent to the original expression with like terms.
Exploring Further: More Complex Equivalents
While factoring out the GCF provides a concise and commonly used equivalent expression, there are infinitely many other equivalent expressions, especially when dealing with more complex scenarios involving multiple variables and operations. For example, let's consider adding or subtracting terms that cancel each other out:
8x - 12y + 32 + 5x - 5x
This adds and subtracts 5x, which effectively adds zero and maintains equivalence with the original expression.
Similarly,
8x - 12y + 32 + 2y - 2y +7 -7
These seemingly more complex forms still maintain equivalence to the original 8x - 12y + 32. The key is to carefully apply algebraic properties to ensure that the changes made only involve adding or subtracting zero or multiplying or dividing by one – actions that maintain equality.
The Importance of Understanding Equivalent Expressions
The ability to identify and manipulate equivalent expressions is not merely an academic exercise. It forms the bedrock of many advanced mathematical concepts and practical applications, such as:
- Solving Equations: Equivalent expressions are crucial in manipulating equations to isolate variables and find solutions.
- Simplifying Complex Expressions: Finding equivalent expressions simplifies complex calculations and makes them easier to understand and work with.
- Graphing Functions: Understanding equivalent expressions allows for different representations of the same function, which can aid in visualizing and interpreting data.
- Calculus: The principles of equivalent expressions are fundamental in the study of limits, derivatives, and integrals.
Frequently Asked Questions (FAQ)
Q: Can any number be factored out of 8x - 12y + 32?
A: While 4 is the greatest common factor, other factors are possible but will result in expressions that are not fully simplified. For instance, you could factor out 2, resulting in 2(4x - 6y + 16). However, this expression can be further simplified by factoring out another 2. Therefore, 4 is the most efficient factor to use.
Q: Is there a single "correct" equivalent expression?
A: No. There are infinitely many equivalent expressions. Factoring out the GCF provides a simplified form, but rearranging terms or adding zero in creative ways generates other equivalent expressions. The "best" equivalent expression often depends on the context of the problem and the desired level of simplification.
Q: How can I check if two expressions are truly equivalent?
A: Substitute several different values for the variables (x and y) into both expressions. If they consistently yield the same results, it strongly suggests equivalence. However, this is not a foolproof method for proving equivalence because it doesn't test all possible values. Rigorous mathematical proofs are necessary for absolute certainty.
Q: Why is this concept important for higher-level math?
A: The ability to manipulate expressions and maintain equivalence is fundamental in more advanced math courses, such as calculus and linear algebra. The foundation you build by mastering these concepts will be essential for your success in those areas.
Conclusion
Finding equivalent expressions is a cornerstone of algebraic manipulation. This article has explored several methods for determining equivalents to 8x - 12y + 32, emphasizing the importance of factoring, the commutative property, the additive identity, and the distributive property. We’ve seen that there are numerous equivalent forms, and the choice of which to use often depends on the context. By mastering these techniques, you'll not only build a strong foundation in algebra but also enhance your problem-solving skills for more complex mathematical challenges ahead. Remember, practice is key – the more you work with equivalent expressions, the more intuitive and efficient your manipulations will become.
Latest Posts
Latest Posts
-
Round 0 97 To The Nearest Tenth
Sep 14, 2025
-
Why Did Feudalism Develop As A Political And Social System
Sep 14, 2025
-
Diagram Of Energy States And Transitions In The Hydrogen Atom
Sep 14, 2025
-
Horizontal Analysis Examines Trends In A Company
Sep 14, 2025
-
How To Find Range Of Square Root Function
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Which Expression Is Equivalent To 8x-12y+32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.