60 Percent Of What Number Is 15
faraar
Sep 21, 2025 · 5 min read
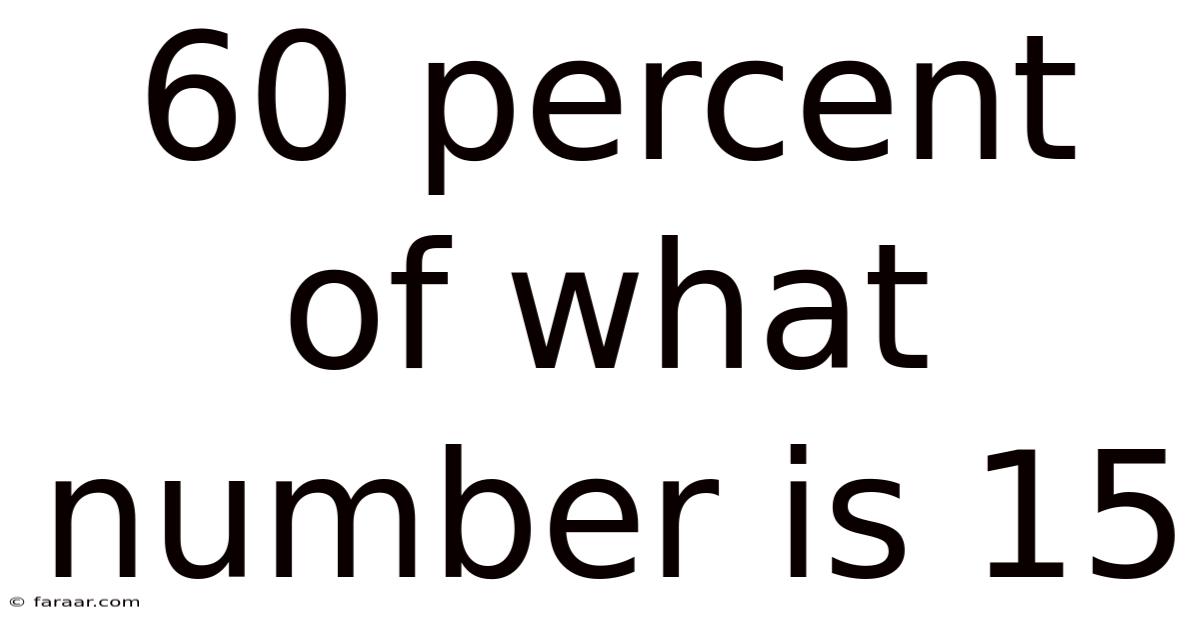
Table of Contents
60 Percent of What Number is 15? Unlocking the Power of Percentages
Finding an unknown number when you know a percentage of it is a common problem encountered in various fields, from everyday budgeting to complex scientific calculations. This article will thoroughly explain how to solve the problem "60 percent of what number is 15?", covering the fundamental concepts, multiple solution methods, real-world applications, and frequently asked questions. Understanding this seemingly simple problem unlocks a deeper understanding of percentage calculations and their practical implications.
Understanding the Problem: Deconstructing "60 Percent of What Number is 15?"
The statement "60 percent of what number is 15?" is essentially a mathematical equation in disguise. Let's break it down:
- 60 percent: This represents a fraction, specifically 60/100 or 3/5. Percentages are simply a way to express a fraction out of 100.
- of: In mathematical terms, "of" implies multiplication.
- What number: This is our unknown variable, which we'll represent with 'x'.
- is 15: This indicates the result of the calculation, which equals 15.
Therefore, the complete mathematical representation of the problem is: (60/100) * x = 15, or 0.6x = 15.
Method 1: Solving Using Algebra
This is the most straightforward and widely used method. We'll use the equation we derived: 0.6x = 15.
-
Isolate the variable: Our goal is to get 'x' by itself on one side of the equation. To do this, we divide both sides of the equation by 0.6:
x = 15 / 0.6
-
Perform the division: Dividing 15 by 0.6 gives us:
x = 25
Therefore, 60 percent of 25 is 15.
Method 2: Solving Using Proportions
This method involves setting up a proportion, which is a statement of equality between two ratios.
-
Set up the proportion: We know that 60 out of 100 is equivalent to 15 out of our unknown number (x). We can express this as:
60/100 = 15/x
-
Cross-multiply: To solve for x, we cross-multiply:
60 * x = 100 * 15
-
Simplify:
60x = 1500
-
Solve for x: Divide both sides by 60:
x = 1500 / 60
x = 25
Again, we find that x = 25.
Method 3: Solving Using the Percentage Formula
The basic percentage formula is: (Part/Whole) * 100 = Percentage. We can rearrange this formula to solve for the "Whole" (our unknown number).
-
Rearrange the formula: We need to solve for "Whole," so let's rearrange the formula:
Whole = (Part / Percentage) * 100
-
Substitute the values: In our problem, the "Part" is 15, and the "Percentage" is 60. Substituting these values, we get:
Whole = (15 / 60) * 100
-
Calculate:
Whole = 0.25 * 100
Whole = 25
Once again, we arrive at the solution: x = 25.
Real-World Applications of Percentage Calculations
Understanding how to solve problems like "60 percent of what number is 15?" has numerous real-world applications:
- Finance: Calculating discounts, interest rates, profit margins, and tax amounts all rely heavily on percentage calculations. For example, if a store offers a 60% discount and an item costs $15 after the discount, you can use this method to determine the original price.
- Science: Percentages are used extensively in various scientific fields, such as chemistry (concentration calculations), biology (population growth), and physics (efficiency calculations).
- Statistics: Percentages are fundamental to expressing and interpreting statistical data, helping researchers to understand trends and make informed decisions.
- Everyday Life: From calculating tips in restaurants to understanding sale prices in shops, percentage calculations are integral to navigating daily life.
Further Exploration: Variations and Extensions
The core concept we've explored can be extended to various scenarios:
- Different Percentages: The same methods can be applied to problems involving different percentages. For example, "35% of what number is 7?" can be solved using the same algebraic, proportional, or percentage formula approaches.
- Finding the Percentage: You can also use these methods to find the percentage if you know the part and the whole. For example, "15 is what percent of 25?"
- Finding the Part: Conversely, you can find the part if you know the percentage and the whole. For example, "What is 60% of 25?"
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this?
A: Absolutely! Calculators can significantly simplify the arithmetic involved, particularly when dealing with more complex percentages or larger numbers.
Q: Are there other ways to solve this problem?
A: While the methods outlined are the most common and efficient, you could potentially use iterative methods (trial and error), though these are less precise and more time-consuming.
Q: What if the percentage is greater than 100%?
A: The same principles apply, but the resulting unknown number will be greater than the given "part". For instance, "150% of what number is 30?" would yield a smaller number than 30.
Q: What if I'm dealing with very large numbers or decimals?
A: The algebraic and proportional methods remain applicable, but using a calculator becomes highly recommended for accuracy and efficiency.
Conclusion: Mastering Percentage Calculations
The seemingly simple question, "60 percent of what number is 15?", opens a gateway to understanding the fundamental principles of percentage calculations. Mastering these calculations is not merely about solving mathematical problems; it's about developing a skill applicable in numerous contexts. By employing the algebraic, proportional, or formula methods, you can confidently tackle a wide range of percentage-related problems, empowering you to navigate financial decisions, interpret scientific data, and engage effectively in everyday life. Remember the core concepts: percentages are fractions, "of" implies multiplication, and algebraic manipulation is key to isolating the unknown variable. Practice these methods, and you'll find yourself confidently solving percentage problems in no time.
Latest Posts
Latest Posts
-
What Is One Third Of One Half
Sep 21, 2025
-
Complete The Function Table For Each Equation
Sep 21, 2025
-
4x 2y 8 Solve For Y
Sep 21, 2025
-
Calculate The Molarity Of Lead In A 9 0 Ppb Solution
Sep 21, 2025
-
Atomic Mass Is Equal To The Number Of
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 60 Percent Of What Number Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.