4 Is 80 Of What Number
faraar
Sep 22, 2025 · 5 min read
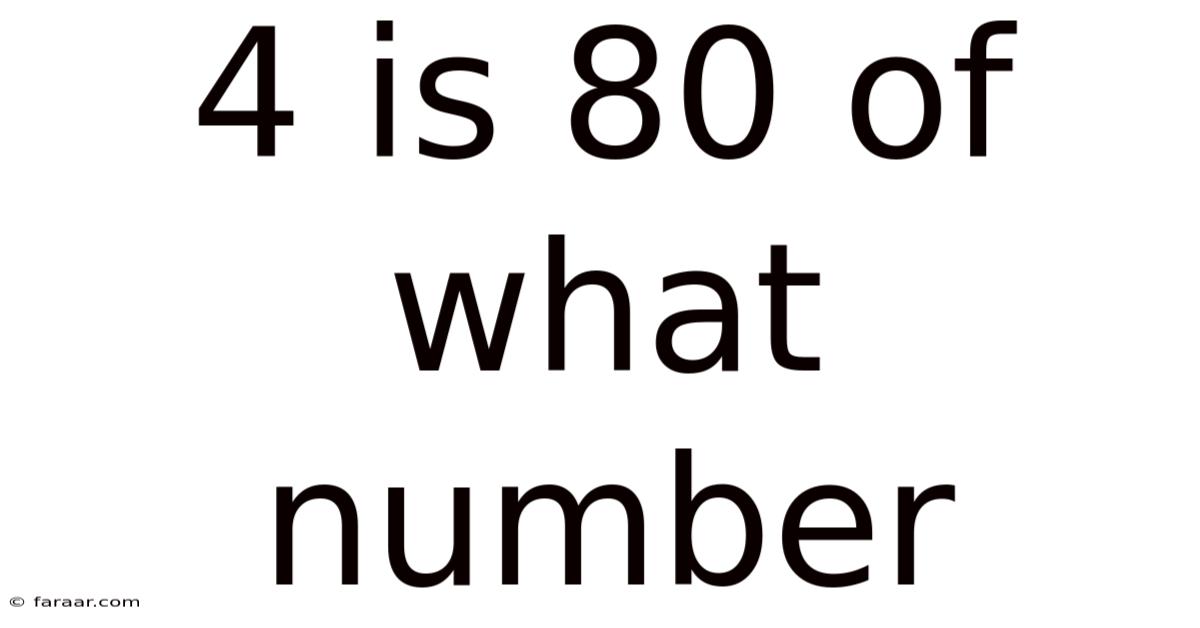
Table of Contents
4 is 80% of What Number? Unlocking the Power of Percentages
Finding an unknown number based on a percentage is a fundamental concept in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding statistical data and financial projections. This article will guide you through solving the problem "4 is 80% of what number?" step-by-step, exploring different approaches, and highlighting the underlying mathematical principles. We’ll delve into various methods, explaining each in detail and providing practical examples to solidify your understanding. By the end, you'll not only know the answer but also possess a deeper understanding of percentage calculations.
Understanding the Problem
The core of the problem "4 is 80% of what number?" lies in translating the words into a mathematical equation. We're given a part (4), a percentage (80%), and we need to find the whole (the unknown number). Understanding this relationship is crucial for solving similar percentage problems.
Method 1: Using the Percentage Formula
The most straightforward approach involves using the basic percentage formula:
Part = Percentage × Whole
In our case:
- Part = 4
- Percentage = 80% = 0.80 (Remember to convert the percentage to a decimal by dividing by 100)
- Whole = x (This is the unknown number we want to find)
Substituting these values into the formula, we get:
4 = 0.80 × x
To solve for x, we divide both sides of the equation by 0.80:
x = 4 / 0.80
x = 5
Therefore, 4 is 80% of 5.
Method 2: Working with Fractions
Percentages can also be expressed as fractions. 80% is equivalent to 80/100, which simplifies to 4/5. We can rewrite the problem as:
4 is (4/5) of what number?
Let's represent the unknown number as 'x'. The equation becomes:
4 = (4/5) * x
To solve for x, we multiply both sides by the reciprocal of 4/5, which is 5/4:
x = 4 * (5/4)
x = 5
Again, we arrive at the solution: 4 is 80% of 5.
Method 3: Proportions
Another effective method involves setting up a proportion. We can express the relationship as:
4/x = 80/100
This proportion states that the ratio of the part (4) to the whole (x) is equal to the ratio of the percentage (80) to 100.
To solve for x, we cross-multiply:
4 * 100 = 80 * x
400 = 80x
Now, divide both sides by 80:
x = 400 / 80
x = 5
Once more, the solution confirms that 4 is 80% of 5.
Method 4: Using a Calculator
While the previous methods demonstrate the underlying mathematical principles, a calculator can efficiently solve percentage problems. Most calculators have a percentage function. You can input the problem directly as:
4 ÷ 80% = 5
This method is practical for quick calculations, but it's important to understand the underlying mathematical concepts for more complex percentage problems.
Practical Applications and Real-World Examples
Understanding percentage calculations is vital in numerous real-world scenarios:
-
Sales and Discounts: Imagine a store offering an 80% discount on an item. If the discounted price is $4, you can use these methods to determine the original price ($5).
-
Financial Planning: Calculating interest earned on savings accounts or interest paid on loans often involves percentage calculations.
-
Statistical Analysis: Percentages are frequently used to represent data and proportions in various fields, such as demographics, market research, and scientific studies.
-
Grade Calculations: If you scored 4 points out of a possible 5 points on a quiz, and this represents 80% of the total possible points, you have successfully grasped the concept of percentage calculation demonstrated in this problem.
Expanding Your Understanding: Working with Different Percentages
Let’s explore how these methods can be applied to other percentage problems. Consider these examples:
- Example 1: 6 is 30% of what number?
Using the formula: 6 = 0.30 * x => x = 6/0.30 = 20
- Example 2: 15 is 75% of what number?
Using proportions: 15/x = 75/100 => 1500 = 75x => x = 20
- Example 3: 2 is 20% of what number?
Using the fraction method: 2 = (20/100) * x => 2 = (1/5) * x => x = 10
These examples demonstrate the versatility and applicability of the methods discussed earlier. The core principle remains consistent: identifying the part, percentage, and the unknown whole, and then employing an appropriate method to solve for the unknown.
Frequently Asked Questions (FAQ)
Q1: Why is it important to convert percentages to decimals or fractions?
A1: To perform mathematical operations, percentages must be expressed as decimals or fractions. Percentages represent a proportion out of 100, and decimals and fractions provide a numerical representation that can be used in calculations.
Q2: Can I use any of these methods to solve any percentage problem?
A2: Yes, the methods outlined here (using the formula, fractions, proportions, and a calculator) are applicable to a wide range of percentage problems. However, some methods might be more efficient than others depending on the complexity of the problem.
Q3: What if the percentage is greater than 100%?
A3: The same principles apply, but the unknown number will be larger than the "part." For example, if 6 is 150% of a number, you will find that the unknown number is smaller than 6.
Q4: What are some common mistakes to avoid when solving percentage problems?
A4: Common mistakes include: incorrectly converting percentages to decimals, using the wrong formula, and errors in calculations. Always double-check your work and ensure that your answer makes logical sense in the context of the problem.
Conclusion
Solving the problem "4 is 80% of what number?" not only provides the answer (5) but also reinforces a fundamental understanding of percentage calculations. Mastering this concept is crucial for success in mathematics and countless real-world applications. By understanding and applying the different methods described – using the formula, working with fractions, setting up proportions, and employing a calculator – you'll gain confidence in tackling percentage problems of varying complexity. Remember to always double-check your work and consider the context of the problem to ensure your answer is both accurate and logical. The ability to solve percentage problems accurately and efficiently empowers you to navigate various scenarios confidently and make informed decisions.
Latest Posts
Latest Posts
-
Given That Abc Def Solve For X
Sep 23, 2025
-
Find The Measure Of Each Labeled Angle
Sep 23, 2025
-
Y 2x 5 Solve For Y
Sep 23, 2025
-
Do Quotations Go After A Comma
Sep 23, 2025
-
How To Find The Orthocenter Of A Triangle With Coordinates
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 4 Is 80 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.