Y 2x 5 Solve For Y
faraar
Sep 23, 2025 · 7 min read
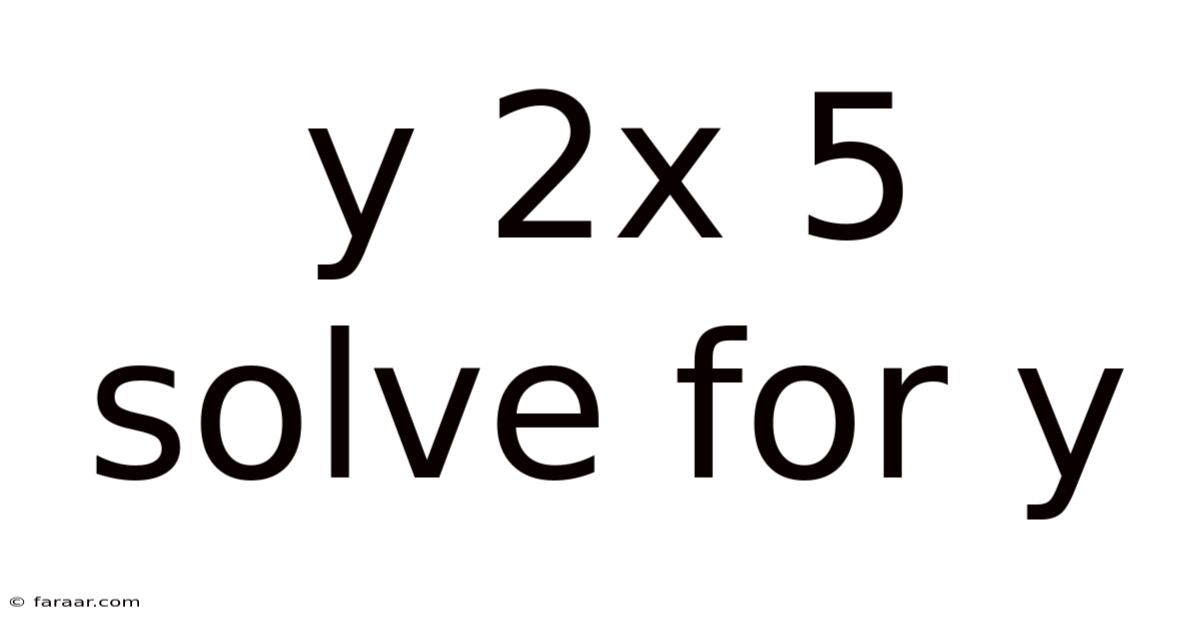
Table of Contents
Solving for Y: A Deep Dive into the Equation y = 2x + 5
This article provides a comprehensive guide on how to solve for y in the linear equation y = 2x + 5, covering various aspects from basic algebraic manipulation to its graphical representation and real-world applications. We’ll explore the fundamental concepts, delve into the steps involved in solving for y, and address frequently asked questions, ensuring a thorough understanding for learners of all levels. This explanation will go beyond simply finding the solution and explore the underlying mathematical principles.
Introduction: Understanding the Equation
The equation y = 2x + 5 represents a linear relationship between two variables, x and y. This is a fundamental concept in algebra and forms the basis for understanding many real-world phenomena. This equation is in slope-intercept form, where the coefficient of x (2 in this case) represents the slope of the line, and the constant term (5) represents the y-intercept – the point where the line crosses the y-axis.
Understanding this form is crucial because it immediately tells us several key properties of the line represented by the equation. The slope indicates the rate of change of y with respect to x. In this instance, a slope of 2 means that for every one-unit increase in x, y increases by two units. The y-intercept indicates the value of y when x is equal to zero.
Solving for y in this equation, however, is remarkably straightforward because the equation is already explicitly solved for y. The value of y directly depends on the value of x. To find y, all we need to do is substitute a value for x and perform the calculation. But let’s explore this in more depth.
Solving for Y: A Step-by-Step Guide
While the equation is already solved for y, let's address the scenario where the equation is presented in a less direct format requiring manipulation to isolate y. For example, let’s consider a slightly more complex version:
2x - y = -5
To solve for y, we need to isolate it on one side of the equation. Here's how:
-
Add y to both sides: This step moves the y term to the right side of the equation. The equation becomes: 2x = y - 5.
-
Add 5 to both sides: This step isolates the y term. The equation becomes: 2x + 5 = y.
-
Rewrite the equation: Finally, we rewrite the equation with y on the left side: y = 2x + 5.
This is the same equation we started with, demonstrating the equivalence. However, this exercise highlights the process of manipulating equations to isolate a specific variable. This process is essential when dealing with more complex equations.
Finding Specific Values of Y
Now that we have our equation, y = 2x + 5, let's explore how to find specific values of y given different values of x.
-
If x = 0: Substitute x = 0 into the equation: y = 2(0) + 5 = 5. Therefore, when x = 0, y = 5. This is the y-intercept.
-
If x = 1: Substitute x = 1 into the equation: y = 2(1) + 5 = 7. Therefore, when x = 1, y = 7.
-
If x = -2: Substitute x = -2 into the equation: y = 2(-2) + 5 = 1. Therefore, when x = -2, y = 1.
-
If x = 5: Substitute x = 5 into the equation: y = 2(5) + 5 = 15. Therefore, when x = 5, y = 15.
These examples demonstrate how to use the equation to determine corresponding y values for various x values. This is a fundamental skill in algebra and has broad applications across many fields.
The Graphical Representation: Visualizing the Relationship
The equation y = 2x + 5 can be represented graphically as a straight line. The slope (2) determines the steepness of the line, and the y-intercept (5) determines where the line crosses the y-axis.
To plot the line, you would typically plot at least two points and draw a straight line through them. We already calculated some points above: (0, 5), (1, 7), (-2, 1), and (5, 15). Plotting these points on a coordinate plane and connecting them will yield a straight line with a positive slope, indicating a positive correlation between x and y. This visual representation provides a clear picture of the relationship described by the equation.
Real-World Applications: Where This Equation Matters
The seemingly simple equation y = 2x + 5 has numerous real-world applications. Here are a few examples:
-
Cost Calculations: Imagine a taxi fare where there's a base fare of $5 and a charge of $2 per mile. Here, x represents the number of miles, and y represents the total cost. The equation y = 2x + 5 accurately models the total cost.
-
Sales Commissions: A salesperson earns a base salary of $5,000 and a commission of $2 for each item sold. x represents the number of items sold, and y represents the total earnings. The equation again provides a straightforward model.
-
Temperature Conversion (Simplified): While not a perfect representation, this equation could serve as a simplified model for converting temperatures between two scales, particularly within a limited range. Adjusting the slope and intercept could provide a reasonable approximation for a particular range.
-
Linear Growth/Decay Models: Many phenomena exhibit linear growth or decay patterns. While more complex equations are often needed, simplified scenarios can be effectively modeled using such a linear equation.
These are just a few examples. The principle of a linear relationship between two variables applies to various scenarios across diverse disciplines, highlighting the equation’s significance.
Solving for X: A Related Problem
While this article focuses on solving for y, it’s also useful to understand how to solve for x. This requires rearranging the equation:
-
Subtract 5 from both sides: y - 5 = 2x
-
Divide both sides by 2: (y - 5) / 2 = x
-
Rewrite the equation: x = (y - 5) / 2
Now, we can use this new equation to find the value of x given a specific value of y. For example, if y = 11, then x = (11 - 5) / 2 = 3. This shows the inverse relationship between the two variables.
Advanced Concepts and Extensions
While the equation y = 2x + 5 is relatively simple, it serves as a foundation for understanding more complex algebraic concepts. Building on this knowledge, we can explore:
-
Systems of Linear Equations: This involves solving multiple linear equations simultaneously to find the values of multiple variables.
-
Quadratic Equations: These equations involve squared terms (e.g., y = x² + 2x + 5), resulting in parabolic curves rather than straight lines.
-
Linear Inequalities: Instead of an equals sign, an inequality sign (<, >, ≤, ≥) is used, resulting in a shaded region on a graph representing the solution set.
-
Calculus: Understanding linear equations is crucial for exploring concepts in calculus such as derivatives and integrals.
Understanding this fundamental equation builds a solid foundation for more advanced mathematical studies.
Frequently Asked Questions (FAQ)
Q: What does the "2" in the equation represent?
A: The "2" is the slope of the line. It indicates that for every one-unit increase in x, y increases by two units.
Q: What does the "5" in the equation represent?
A: The "5" is the y-intercept. It's the point where the line crosses the y-axis (where x = 0).
Q: Can this equation be used to model any real-world situation?
A: While many real-world situations can be approximated using a linear model, not all situations are perfectly linear. The suitability of this equation depends on the specific situation.
Q: What if the equation is not in the y = mx + b form?
A: You will need to use algebraic manipulation, like the example given earlier, to isolate y and put the equation into the slope-intercept form.
Q: What are the limitations of using this simple linear equation?
A: This simple linear model does not account for non-linear relationships or situations where other factors significantly influence the outcome. More complex models might be needed for more intricate scenarios.
Conclusion: Mastering the Fundamentals
Solving for y in the equation y = 2x + 5, while seemingly straightforward, provides a foundational understanding of algebraic manipulation and linear relationships. This simple equation serves as a crucial stepping stone for tackling more complex mathematical problems and applying these concepts to various real-world applications. Mastering this fundamental concept will undoubtedly enhance your problem-solving skills and broader mathematical comprehension. Through understanding its graphical representation and real-world implications, you'll build a robust foundation in algebra and prepare yourself for more advanced mathematical pursuits.
Latest Posts
Latest Posts
-
A Pe Rt Solve For T
Sep 23, 2025
-
How To Solve For A Variable Exponent
Sep 23, 2025
-
An Angle Measuring More Than 90 Degrees
Sep 23, 2025
-
Complete And Balance The Following Precipitation Reactions
Sep 23, 2025
-
How Are Potential Energy Kinetic Energy And Total Energy Related
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Y 2x 5 Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.