What Is 1/2 To The Power Of 3
faraar
Sep 15, 2025 · 6 min read
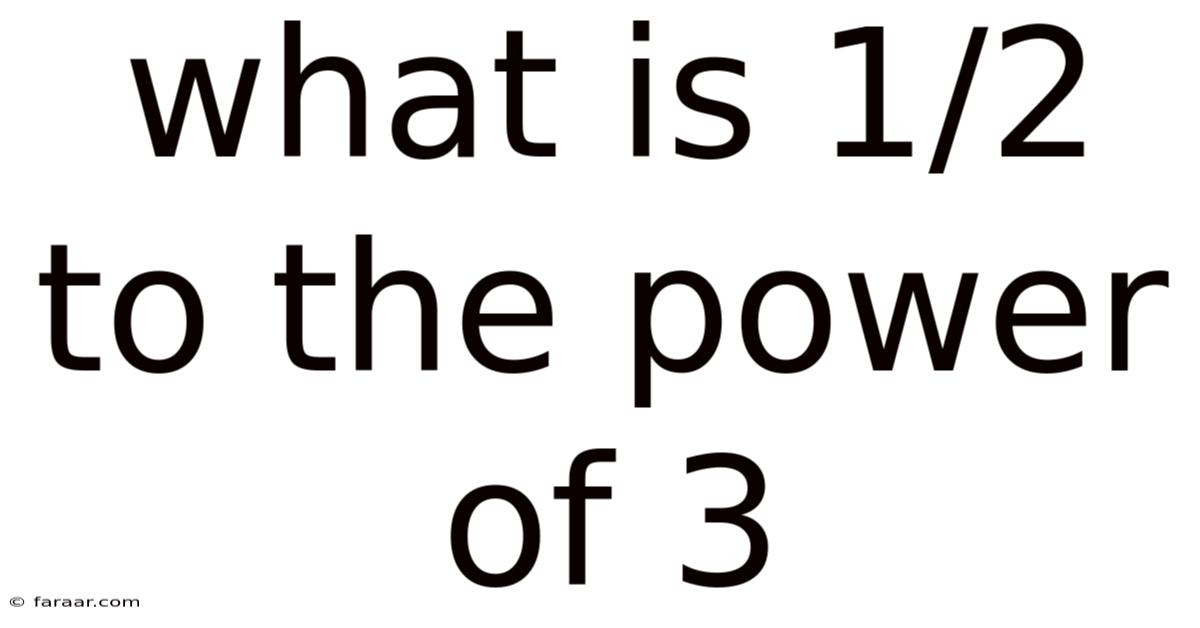
Table of Contents
What is 1/2 to the Power of 3? A Deep Dive into Fractional Exponents
This article explores the seemingly simple question: "What is 1/2 to the power of 3?" While the answer itself is straightforward, delving into the process reveals fundamental concepts in mathematics, particularly regarding fractional exponents and their application. Understanding this seemingly basic calculation unlocks a broader understanding of exponentiation and its various uses in algebra, calculus, and beyond. We will explore the calculation step-by-step, delve into the underlying mathematical principles, address common misconceptions, and even touch upon practical applications of fractional exponents.
Understanding Exponents
Before we tackle 1/2 to the power of 3, let's refresh our understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. For example:
- 2³ means 2 multiplied by itself three times: 2 x 2 x 2 = 8. Here, 2 is the base, and 3 is the exponent.
- 5² means 5 multiplied by itself two times: 5 x 5 = 25. Here, 5 is the base, and 2 is the exponent.
This principle extends to fractional bases as well. When the base is a fraction, we simply multiply the fraction by itself the number of times indicated by the exponent.
Calculating 1/2 to the Power of 3
Now, let's address the question at hand: What is (1/2)³?
This means we multiply the fraction 1/2 by itself three times:
(1/2)³ = (1/2) x (1/2) x (1/2)
To multiply fractions, we multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(1 x 1 x 1) / (2 x 2 x 2) = 1/8
Therefore, (1/2)³ = 1/8
A Deeper Look: The Rules of Exponents
The calculation above demonstrates a simple application of the rules of exponents. Let's examine some key rules that apply to this and more complex scenarios:
- Product Rule: When multiplying exponential expressions with the same base, we add the exponents: aᵐ x aⁿ = aᵐ⁺ⁿ
- Quotient Rule: When dividing exponential expressions with the same base, we subtract the exponents: aᵐ / aⁿ = aᵐ⁻ⁿ
- Power Rule: When raising an exponential expression to another power, we multiply the exponents: (aᵐ)ⁿ = aᵐⁿ
- Zero Exponent Rule: Any non-zero number raised to the power of zero is equal to 1: a⁰ = 1
- Negative Exponent Rule: A number raised to a negative exponent is equal to its reciprocal raised to the positive exponent: a⁻ⁿ = 1/aⁿ
These rules are crucial for understanding and manipulating expressions involving exponents, including those with fractional bases.
Fractional Exponents: Extending the Concept
The concept of exponents extends beyond whole numbers. We can also have fractional exponents, such as (1/2)³, which we've already solved. Fractional exponents are closely related to roots. For example:
- a¹/² = √a (the square root of a)
- a¹/³ = ³√a (the cube root of a)
- aᵐ/ⁿ = ⁿ√(aᵐ) (the nth root of a raised to the power of m)
Therefore, (1/2)³ can also be understood as the cube of the square root of 1/2. Although this approach isn't the most practical method for solving this specific problem, it highlights the interconnectedness of exponents and roots.
Misconceptions about Fractional Exponents
A common misconception is that (1/2)³ is the same as (1³/2). This is incorrect. Remember the order of operations – exponents are calculated before multiplication or division. The exponent applies to the entire base, which in this case is the fraction 1/2.
Practical Applications of Fractional Exponents
Fractional exponents appear frequently in various fields, including:
- Physics: Calculating the decay of radioactive materials often involves fractional exponents.
- Finance: Compound interest calculations use exponents to model growth over time.
- Engineering: Many engineering formulas utilize exponents for representing different aspects of design and performance.
- Computer Science: Algorithms and data structures often involve exponential relationships.
Understanding fractional exponents is crucial for mastering these fields and solving real-world problems.
Expanding on the Calculation: Different Bases and Exponents
Let's explore some related calculations to further solidify our understanding:
- (1/3)³: Following the same method as before, (1/3)³ = (1/3) x (1/3) x (1/3) = 1/27
- (2/5)²: (2/5)² = (2/5) x (2/5) = 4/25
- (3/4)⁴: (3/4)⁴ = (3/4) x (3/4) x (3/4) x (3/4) = 81/256
These examples demonstrate the versatility of the method for calculating fractional bases raised to whole number powers. The process remains consistent: multiply the fraction by itself the number of times indicated by the exponent.
Visualizing Fractional Exponents
While not directly applicable to solving (1/2)³, visualizing fractional exponents can help in understanding the concept. Consider representing the fraction 1/2 as a portion of a whole. Cubing this fraction can be visualized as repeatedly subdividing the portion into smaller and smaller pieces, leading to a progressively smaller fraction of the original whole.
Beyond Whole Number Exponents: Irrational and Complex Exponents
Our discussion has focused on whole number exponents. However, the concept of exponents extends to irrational numbers (like π) and even complex numbers. While calculating these more advanced scenarios involves more sophisticated mathematical techniques, the fundamental principles remain the same. The core idea of repeated multiplication applies, even if the number of repetitions or the base itself becomes more abstract.
Frequently Asked Questions (FAQ)
-
Q: What if the exponent is negative?
A: A negative exponent indicates the reciprocal. For example, (1/2)⁻³ = 1 / (1/2)³ = 8. In essence, a negative exponent "flips" the fraction.
-
Q: Can I use a calculator to solve this?
A: Yes, most scientific calculators can handle fractional exponents. You would typically input the calculation as (0.5)^3 or (1/2)^3.
-
Q: Is there a simpler way to calculate this besides repeated multiplication?
A: For simple cases like (1/2)³, repeated multiplication is straightforward. However, for larger exponents, more efficient methods exist, often involving logarithmic functions.
-
Q: Why is understanding fractional exponents important?
A: Understanding fractional exponents is fundamental to many areas of mathematics, science, and engineering. It provides a solid foundation for more advanced mathematical concepts and real-world problem-solving.
Conclusion
The seemingly simple question, "What is 1/2 to the power of 3?" opens the door to a deeper understanding of exponents and their application. By exploring the calculation step-by-step, reviewing the rules of exponents, and understanding the relationship between exponents and roots, we've built a solid understanding not only of this specific calculation but also of broader mathematical concepts. Remember, the power of mathematics lies in its ability to unlock a deeper understanding of the world around us, and mastering fundamental concepts like fractional exponents is a crucial step on that journey. Through practice and continued exploration, you can build confidence and proficiency in handling more complex exponential calculations.
Latest Posts
Latest Posts
-
Write The Integral In Terms Of U
Sep 15, 2025
-
Square That Is Not A Rhombus
Sep 15, 2025
-
28 What Year Was I Born
Sep 15, 2025
-
What Is The Measure Of 4
Sep 15, 2025
-
Which Statement Is Not A Part Of The Cell Theory
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.