3 Less Than 5 Times A Number
faraar
Sep 15, 2025 · 6 min read
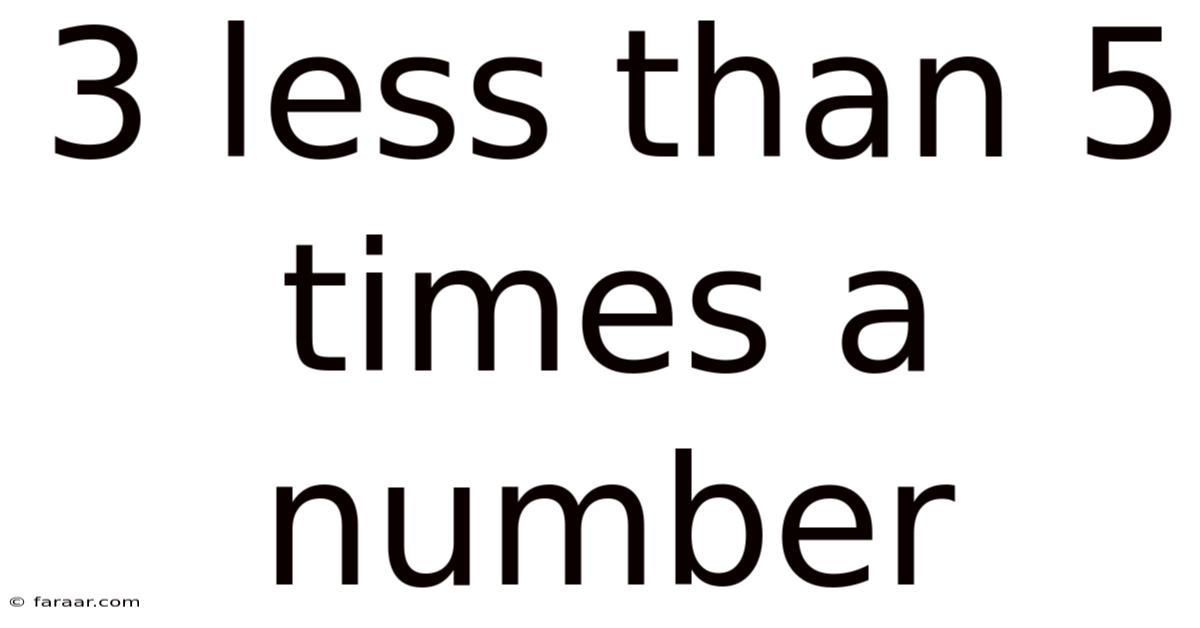
Table of Contents
Decoding "3 Less Than 5 Times a Number": A Deep Dive into Algebraic Expressions
This article explores the mathematical expression "3 less than 5 times a number," breaking down its components, demonstrating how to translate it into an algebraic equation, and solving various related problems. Understanding this seemingly simple phrase requires a grasp of fundamental algebraic concepts, which we will cover in detail, making this a valuable resource for students learning algebra and anyone seeking a deeper understanding of mathematical language. We'll explore different approaches to solving problems involving this expression and address frequently asked questions. The key concepts we will cover include translating word problems into algebraic equations, solving linear equations, and applying these skills to real-world scenarios.
Understanding the Language of Mathematics
Before diving into the specifics of "3 less than 5 times a number," let's establish a foundation in translating mathematical word problems into algebraic expressions. Mathematics relies on precise language; each word carries specific meaning and dictates the operations involved. In this case, we have several key phrases:
-
"A number": This represents an unknown value, which we typically represent with a variable, usually x or n.
-
"5 times a number": This indicates multiplication. "5 times a number" translates directly to 5 * x (or 5n, 5x, etc.).
-
"3 less than": This indicates subtraction, but the order is crucial. "3 less than" means we are subtracting 3 from the preceding quantity.
Translating the Phrase into an Algebraic Equation
Combining these elements, "3 less than 5 times a number" translates to the algebraic expression: 5x - 3. Notice that the subtraction comes after the multiplication, reflecting the order specified in the phrase. This is a common point of confusion, so take your time to fully grasp the meaning of each word and its position within the expression. The difference between "3 less than 5 times a number" and "3 less 5 times a number" (which would translate to 3 - 5x) highlights the importance of order of operations.
Solving Equations Involving the Expression
Now that we have our algebraic expression, let's explore how to solve equations that incorporate it. Suppose we are given the following problem:
"3 less than 5 times a number is equal to 17. Find the number."
This word problem can be translated into the equation:
5x - 3 = 17
To solve for x, we use the principles of algebra:
-
Add 3 to both sides: This isolates the term with x. The equation becomes: 5x = 20
-
Divide both sides by 5: This solves for x. The equation becomes: x = 4
Therefore, the number is 4. We can check our answer by substituting x = 4 back into the original equation: 5(4) - 3 = 17, which is true.
Exploring Variations and More Complex Problems
The phrase "3 less than 5 times a number" can be incorporated into more complex problems. Let's consider these examples:
Example 1: Inequalities
"3 less than 5 times a number is greater than 12. Find the range of possible values for the number."
This translates to the inequality:
5x - 3 > 12
Solving this inequality:
-
Add 3 to both sides: 5x > 15
-
Divide both sides by 5: x > 3
Therefore, the number must be greater than 3.
Example 2: Two-Step Equations
"Twice the result of 3 less than 5 times a number is 26. Find the number."
This problem involves nested operations. Let's break it down:
-
"3 less than 5 times a number": This is still 5x - 3.
-
"Twice the result": This means we multiply the entire expression (5x - 3) by 2.
The equation becomes:
2(5x - 3) = 26
Solving this equation:
-
Distribute the 2: 10x - 6 = 26
-
Add 6 to both sides: 10x = 32
-
Divide both sides by 10: x = 3.2
Therefore, the number is 3.2.
Example 3: Word Problems with Context
Let's consider a real-world application. Imagine a phone plan that costs $3 per month plus $5 per gigabyte of data used. If a user's bill is $17, how many gigabytes did they use? This can be represented by the equation:
5x + 3 = 17 (Note the different order of operations compared to our previous examples)
Solving this equation:
-
Subtract 3 from both sides: 5x = 14
-
Divide both sides by 5: x = 2.8
The user used 2.8 gigabytes of data.
The Importance of Order of Operations (PEMDAS/BODMAS)
Remember the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction)? This dictates the order in which we perform operations in a mathematical expression. In our examples, we carefully followed PEMDAS to ensure correct solutions. Incorrect order of operations will lead to incorrect answers. Always prioritize operations within parentheses first, then exponents, followed by multiplication and division (from left to right), and finally addition and subtraction (from left to right).
Different Representations of the Expression
The expression "3 less than 5 times a number" can be represented in other ways, although they all boil down to the same core algebraic expression. For instance, "5 times a number, reduced by 3" is another way of phrasing it, conveying the same mathematical concept.
Frequently Asked Questions (FAQ)
-
Q: What if the phrase was "5 times a number less 3"? A: This would still translate to 5x - 3. The placement of "less 3" at the end doesn't alter the order of operations.
-
Q: Can I use a different variable instead of x? A: Absolutely! You can use any letter to represent the unknown number, such as n, a, or y.
-
Q: What if the problem involves decimals or fractions? A: The same principles apply. Just be careful with your calculations and remember the rules for working with decimals and fractions.
-
Q: How can I improve my skills in translating word problems into algebraic expressions? A: Practice is key! Work through many different types of word problems, focusing on understanding the meaning of each word and how it translates into a mathematical operation. Break down complex problems into smaller, manageable steps.
Conclusion
Understanding the phrase "3 less than 5 times a number" and its algebraic representation (5x - 3) is fundamental to mastering basic algebra. This involves not only understanding the mathematical operations but also the precise language used to describe them. By practicing translating word problems into equations and applying the principles of algebra, you can confidently solve a wide range of problems involving this expression and similar concepts. Remember to carefully analyze the language, apply the correct order of operations, and practice regularly to build your confidence and mastery of algebra. The journey of learning mathematics is about more than just memorization; it's about developing a deep understanding of how mathematical concepts relate to the real world.
Latest Posts
Latest Posts
-
The Prokaryotic Dna Is Located In The
Sep 15, 2025
-
How To Find The Value Of X And Y
Sep 15, 2025
-
Is 1 3 And 1 3 Equal 2 3
Sep 15, 2025
-
Find The Value Of X Rounded To The Nearest Tenth
Sep 15, 2025
-
20 Of What Number Is 12
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3 Less Than 5 Times A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.