20 Of What Number Is 12
faraar
Sep 15, 2025 · 5 min read
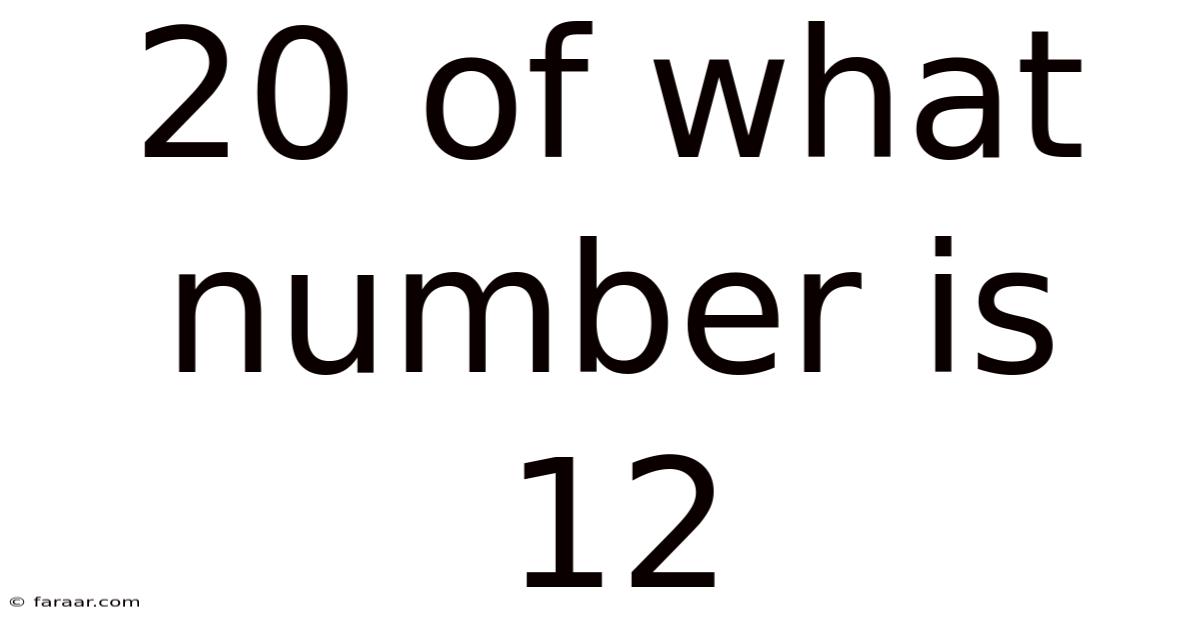
Table of Contents
Unraveling the Mystery: 20% of What Number is 12? A Deep Dive into Percentages
Finding 20% of a number is a common task in everyday life, from calculating discounts to understanding financial reports. This article will not only show you how to solve the equation "20% of what number is 12?" but will also provide a comprehensive understanding of percentages, their applications, and different methods to solve similar problems. We'll delve into the underlying mathematical principles and equip you with the tools to tackle any percentage-related challenge with confidence.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." So, 20% means 20 out of 100, which can be written as a fraction (20/100) or a decimal (0.20). Understanding this fundamental concept is crucial for solving percentage problems.
Method 1: Using the Equation
Let's tackle the core problem: "20% of what number is 12?" We can translate this statement into a mathematical equation:
0.20 * x = 12
Where 'x' represents the unknown number we're trying to find. To solve for x, we follow these steps:
-
Divide both sides of the equation by 0.20: This isolates 'x' on one side of the equation.
x = 12 / 0.20
-
Perform the division: 12 divided by 0.20 equals 60.
Therefore, x = 60
Therefore, 20% of 60 is 12.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. A proportion is a statement that two ratios are equal. We can set up a proportion using the information given:
20/100 = 12/x
This proportion states that the ratio of 20 to 100 is equal to the ratio of 12 to the unknown number (x). To solve for x, we use cross-multiplication:
20 * x = 12 * 100
20x = 1200
x = 1200 / 20
x = 60
Again, we arrive at the answer: 60. This method demonstrates the equivalence between percentages and ratios, providing a versatile approach to percentage calculations.
Method 3: Working Backwards from the Percentage
Since 20% represents 12, we can ask ourselves: "What is 1% of the number?"
-
Find 1%: Divide 12 by 20 (since 20% = 12)
12 / 20 = 0.6
This means 1% of the number is 0.6.
-
Find 100%: Multiply 0.6 by 100 (since 100% represents the whole number)
0.6 * 100 = 60
Once again, the solution is 60. This method is particularly helpful in visualizing the relationship between different percentages of a number.
Expanding Your Understanding: Beyond the Basic Equation
While solving "20% of what number is 12?" is straightforward, understanding the broader context of percentage calculations is essential. Let's explore some related concepts:
-
Finding a Percentage of a Number: This is the inverse operation of our problem. For instance, finding 20% of 60 is a simple multiplication: 0.20 * 60 = 12.
-
Calculating Percentage Increase/Decrease: These calculations are crucial in various fields like finance and economics. For example, if a price increases from $50 to $60, the percentage increase is calculated as follows:
(Increase/Original Price) * 100% = ((60-50)/50) * 100% = 20%
-
Applying Percentages to Real-World Scenarios: Percentages are ubiquitous in our daily lives:
- Discounts: A 25% discount on a $100 item means a saving of $25 (0.25 * $100).
- Taxes: Sales tax is usually expressed as a percentage of the purchase price.
- Interest Rates: Interest earned on savings accounts or paid on loans is calculated as a percentage of the principal amount.
- Statistical Analysis: Percentages are essential in representing data in charts, graphs, and reports.
Practical Applications and Examples
Let's apply our knowledge to some real-world examples:
Example 1: Sales Commission
A salesperson earns a 20% commission on their sales. If they earned $1200 in commission, what was the total value of their sales?
Using the equation: 0.20 * x = 1200, we solve for x: x = 1200 / 0.20 = 6000. The total sales were $6000.
Example 2: Grade Calculation
A student scored 12 out of 20 on a quiz. What is their percentage score?
This involves calculating what percentage 12 represents of 20: (12/20) * 100% = 60%. The student scored 60%.
Example 3: Discount Calculation
A store offers a 20% discount on an item originally priced at $x. The discounted price is $48. What is the original price?
This problem is equivalent to our original question. We know that 80% of the original price ($x) is $48. The equation becomes: 0.80 * x = 48. Solving for x, we find x = 48 / 0.80 = 60. The original price was $60.
Troubleshooting Common Mistakes
Many errors in percentage calculations stem from misunderstandings of the basic principles. Here are some common pitfalls to avoid:
-
Incorrect Conversion of Percentages to Decimals: Always remember to convert percentages to decimals (e.g., 20% = 0.20) before performing calculations.
-
Mixing up Percentages and Decimal Places: Maintain consistency in your units. Avoid mixing percentages and decimals without proper conversion.
-
Not Understanding the Context: Pay close attention to the wording of the problem. Make sure you understand what is being asked.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to solve percentage problems?
Yes, absolutely! Calculators are very helpful, particularly for more complex problems. Many calculators have a percentage function that simplifies the calculations.
Q2: Are there other methods to solve percentage problems?
Yes, there are several other approaches, including using ratios, proportions, and even visual aids like diagrams or charts. The best method often depends on the specific problem and your personal preference.
Q3: What if the percentage is not a whole number (e.g., 17.5%)?
The principles remain the same. You'll simply use the decimal equivalent (0.175) in your calculations.
Q4: How can I improve my understanding of percentages?
Practice is key! Work through many different examples, starting with simple ones and gradually increasing the complexity. You can find plenty of practice problems online or in textbooks.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a crucial skill for success in many areas of life. From managing finances to interpreting data, the ability to solve percentage problems efficiently and accurately is invaluable. By mastering the different methods presented in this article, you'll be equipped to confidently tackle any percentage-related challenge, whether it's determining discounts, calculating interest, or analyzing statistical data. Remember to practice regularly, and you'll find yourself effortlessly navigating the world of percentages. The solution to "20% of what number is 12?" – 60 – is just the beginning of your journey to mastering this essential mathematical concept.
Latest Posts
Latest Posts
-
Difference Between Drawing And Sketch Paper
Sep 15, 2025
-
Which Expression Is Equivalent To 3 2
Sep 15, 2025
-
How To Solve For The Hypotenuse
Sep 15, 2025
-
What Is A Quarter In Decimal
Sep 15, 2025
-
How To Find The Perimeter Of An Isosceles Triangle
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 20 Of What Number Is 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.