3 4 1 2n 5 8
faraar
Aug 25, 2025 · 6 min read
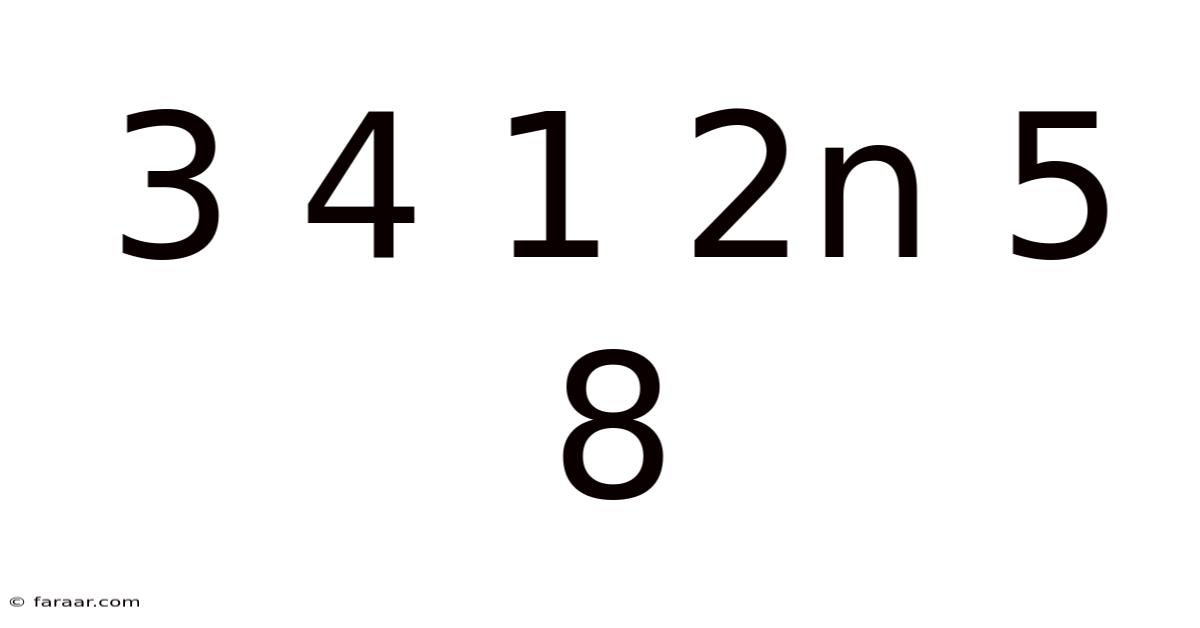
Table of Contents
Decoding the Sequence: Unveiling the Mysteries of 3 4 1 2n 5 8
The seemingly simple sequence "3 4 1 2n 5 8" holds a surprising depth of mathematical and logical possibilities. This article delves into the various interpretations and solutions, exploring the different patterns and rules that could generate this sequence. We'll examine different perspectives, from simple arithmetic progressions to more complex algorithms, highlighting the importance of logical reasoning and pattern recognition in mathematics. Understanding this seemingly random collection of numbers requires a multifaceted approach, embracing creativity and rigorous analysis.
Understanding the Ambiguity: Multiple Interpretations
The beauty of this sequence lies in its inherent ambiguity. Unlike strictly defined sequences with clear rules, "3 4 1 2n 5 8" invites multiple interpretations, showcasing the versatility of mathematical thinking. The presence of "2n" further enhances this ambiguity, acting as a wildcard that can represent various mathematical operations or patterns. Let's explore some plausible interpretations:
1. A Sequence with a Missing Operation
One approach interprets "2n" as a placeholder for an unknown operation or a missing number in an otherwise consistent sequence. This approach requires us to identify a pattern within the known numbers (3, 4, 1, 5, 8) and then deduce the missing operation or value based on that pattern. Several patterns could be considered:
-
Alternating Differences: Consider the differences between consecutive numbers: 1 (4-3), -3 (1-4), 4 (5-1), 3 (8-5). While no immediate pattern emerges, we could speculate that the differences alternate between positive and negative values, suggesting a missing negative number between 1 and 5 to maintain this alternation. This would lead to a series of alternating differences like 1, -3, -x, 4, 3, where 'x' needs to be a positive number to continue the alternating sign pattern. However, this still leaves "2n" undefined.
-
Modular Arithmetic: The sequence could be related to modular arithmetic, where numbers cycle through a specific range. However, with only five distinct numbers, it's difficult to definitively establish a modulus.
-
Combination of Arithmetic and Geometric Progressions: Perhaps the sequence is a hybrid, combining elements of arithmetic and geometric progressions. Identifying such a combined pattern requires extensive analysis and possibly a trial-and-error approach, considering various arithmetic and geometric operations on the existing numbers.
2. "2n" as a Variable Representing a Rule
Alternatively, "2n" can be interpreted as a variable within a formula or rule that governs the sequence. This approach requires us to find a rule that produces the given numbers when specific values are substituted for "n." Several possibilities exist:
-
Recursive Relationship: The sequence could be defined recursively, where each term depends on one or more preceding terms. This might involve a complex formula incorporating "n" to generate each term. Finding such a recursive relationship often involves trial and error and careful observation of the differences between consecutive terms or other potential patterns.
-
Polynomial Approximation: A polynomial function could approximate the sequence. If we treat the given numbers as y-values corresponding to x-values (1, 2, 3, 4, 5...), we could use polynomial regression techniques to find a polynomial function that fits the data. The coefficient of the "x" term might correspond to "2n" in the original sequence. However, the accuracy of this approximation depends on the nature of the underlying sequence.
-
Piecewise Function: A piecewise function, which defines different rules for different sections of the sequence, could be another viable interpretation. For instance, one rule might apply to the first three terms, and a different rule to the remaining terms, integrating "2n" appropriately into the piecewise definition.
3. Interpreting "n" as a Specific Value or a Range
We must also consider the meaning of "n." Does "n" represent a single specific integer, or could it represent a range of integers? If it’s a specific value, then the sequence needs to be modified to be consistent. If it represents a range, then we need to determine what that range might be, and how the output of the formula changes with different "n" values within that range.
For instance, if "2n" means "2 multiplied by n", a range of values for "n" might be needed to generate the entire sequence, or to generate the other numbers not explicitly listed.
Applying Logical Reasoning and Pattern Recognition
Solving this sequence puzzle requires systematic logical reasoning and keen pattern recognition skills. The following steps illustrate a structured approach:
-
Analyze the differences and ratios: Calculate the differences between consecutive numbers and examine the ratios between them. Look for any consistent patterns in these differences or ratios.
-
Consider various mathematical operations: Explore different arithmetic and algebraic operations that might link the numbers in the sequence. Consider addition, subtraction, multiplication, division, powers, and factorials.
-
Look for repeating patterns: Investigate whether the sequence contains repeating patterns or sub-sequences that could hold clues to its structure.
-
Use trial and error: Experiment with different rules and formulas to see if they can generate the given sequence or a similar pattern.
Advanced Mathematical Approaches
For more complex scenarios, advanced mathematical techniques such as:
-
Discrete Mathematics: Exploring concepts like recurrence relations, generating functions, and graph theory might reveal hidden relationships.
-
Number Theory: Investigating prime factorization, divisibility rules, and other number-theoretic properties could unlock patterns in the sequence.
-
Statistical Analysis: If the sequence appears random, statistical methods might help identify underlying distributions or tendencies that could provide insights.
Frequently Asked Questions (FAQ)
Q: Is there a single definitive answer to this sequence?
A: No. The ambiguity of "2n" and the lack of additional information make multiple interpretations possible. The "correct" answer depends on the context or assumptions applied.
Q: How can I improve my pattern recognition skills?
A: Practice is key. Solve various mathematical puzzles and sequences. Start with simpler ones and gradually work towards more complex problems. Analyzing the solutions to problems you don't immediately understand helps sharpen your pattern recognition skills.
Q: What if additional numbers were added to the sequence?
A: Additional numbers would provide more information, potentially narrowing down the possible interpretations and leading to a more definitive solution or a refined understanding of the underlying pattern.
Conclusion: The Power of Ambiguity and Logical Deduction
The sequence "3 4 1 2n 5 8" serves as a compelling example of how a seemingly simple problem can open up a vast landscape of mathematical possibilities. Its ambiguity challenges our assumptions and forces us to employ critical thinking and creative problem-solving skills. By applying various mathematical concepts, logical reasoning, and pattern recognition techniques, we can explore multiple valid interpretations. Ultimately, the exercise highlights the importance of embracing ambiguity and the power of deductive reasoning in unraveling mathematical mysteries. This journey of exploration underscores that mathematics is not just about finding the "right" answer, but also about the process of discovery and the development of our problem-solving abilities. The flexibility inherent in the sequence underscores the richness and complexity within even apparently simple numerical patterns, encouraging a deeper investigation into mathematical thought and exploration.
Latest Posts
Latest Posts
-
How Do You Say Thank You In Muslim
Aug 25, 2025
-
44 Is What Percent Of 50
Aug 25, 2025
-
Define The Era Of Good Feelings
Aug 25, 2025
-
Y Square Root Of X 2
Aug 25, 2025
-
Whats 50 Degrees Celsius In Fahrenheit
Aug 25, 2025
Related Post
Thank you for visiting our website which covers about 3 4 1 2n 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.