Y Square Root Of X 2
faraar
Aug 25, 2025 · 6 min read
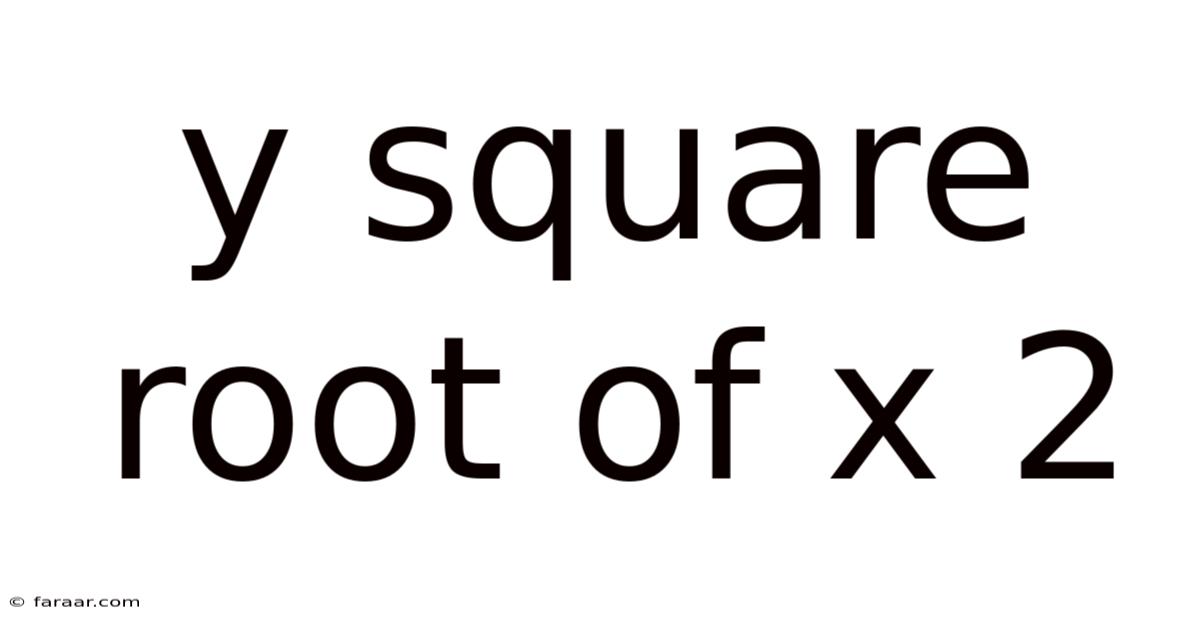
Table of Contents
Decoding the Mystery: A Deep Dive into y = √x²
Understanding the equation y = √x² might seem straightforward at first glance, but a closer look reveals intriguing nuances and important mathematical concepts. This comprehensive guide will explore this equation in detail, clarifying its meaning, exploring its implications, and addressing common misconceptions. We'll delve into its graphical representation, its relationship to absolute values, and its applications in various mathematical fields. By the end, you'll have a solid grasp of this seemingly simple, yet surprisingly complex, mathematical relationship.
Introduction: Unveiling the Square Root and its Implications
The equation y = √x² involves two fundamental mathematical operations: squaring (x²) and taking the square root (√). Squaring a number means multiplying it by itself (x * x), while the square root of a number is a value that, when multiplied by itself, gives the original number. The seemingly simple combination of these operations, however, leads to some interesting considerations, particularly concerning the concept of the principal square root.
The principal square root is always non-negative. This means that even if we are dealing with a negative number initially, the square root operation will always produce a positive result or zero. This is crucial in understanding the behavior of y = √x².
Understanding the Graphical Representation
To fully grasp the equation y = √x², let's visualize it graphically. Plotting points on a Cartesian plane will reveal its unique characteristics.
-
Positive x-values: When x is positive (x > 0), x² is positive, and the square root of a positive number is also positive. Therefore, y = x. The graph in this quadrant mirrors a straight line with a slope of 1, passing through the origin (0,0).
-
Negative x-values: When x is negative (x < 0), x² is positive (a negative number multiplied by itself results in a positive number). However, the principal square root function will always return a positive value. Thus, y = -x. The graph in this quadrant mirrors a straight line with a slope of -1, also passing through the origin (0,0).
-
The Origin (0,0): At x = 0, x² = 0, and √0 = 0. So the graph passes through the origin.
In summary, the graph of y = √x² is composed of two parts:
- A line with a positive slope (y = x) for x ≥ 0.
- A line with a negative slope (y = -x) for x < 0.
This creates a V-shaped graph, symmetrical around the y-axis. This shape is characteristic of the absolute value function, which we will explore further.
The Connection to Absolute Value: |x|
The equation y = √x² is mathematically equivalent to y = |x|, where |x| represents the absolute value of x. The absolute value of a number is its distance from zero, always resulting in a non-negative value.
- If x ≥ 0: |x| = x.
- If x < 0: |x| = -x.
This explains the V-shaped graph we observed earlier. The absolute value function, and consequently y = √x², always returns a non-negative value for any input x.
Addressing Common Misconceptions
Several misconceptions frequently arise when dealing with y = √x². Let's address some of the most common ones:
-
Misconception 1: √x² = x for all x. This is incorrect. While it's true for non-negative x values, it's false for negative x values. For example, if x = -2, √x² = √(-2)² = √4 = 2, not -2.
-
Misconception 2: The square root always "undoes" the square. This is only true when dealing with non-negative numbers. The square root operation, when applied to the result of squaring a number, returns the absolute value of that number, not necessarily the original number itself.
-
Misconception 3: y = √x² is a simple linear function. While the function appears linear in separate quadrants, its overall shape is a V-shape, reflecting the non-linear behavior of the absolute value function.
Mathematical Properties and Applications
The equation y = √x² exhibits several important mathematical properties:
-
Even Function: The function is even, meaning f(-x) = f(x). This symmetry around the y-axis is evident in its V-shaped graph.
-
Non-negative Range: The range of the function (the set of possible y-values) is y ≥ 0. The function never produces a negative output.
-
Continuous Function: The function is continuous, meaning there are no breaks or jumps in its graph.
Its applications are found in various areas of mathematics and beyond:
-
Geometry: Calculating distances, particularly in coordinate geometry, often involves the absolute value function, which is directly related to y = √x².
-
Calculus: The absolute value function, and hence y = √x², is used in several calculus concepts, including differentiation and integration, although its derivative is not defined at x = 0.
-
Physics and Engineering: Absolute values are essential in representing quantities that are always positive, such as speed (magnitude of velocity).
-
Computer Science: The concept of absolute value is widely utilized in algorithms and programming to handle various numerical operations.
Advanced Considerations: Complex Numbers
While we've primarily focused on real numbers, the concept extends to complex numbers as well. In the realm of complex numbers, the square root of a number can have multiple solutions. However, the principal square root remains defined as the non-negative solution. For instance, √(-2)² still equals 2 in the complex number system, even though the intermediate steps may involve imaginary numbers.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between y = √x² and y = x? A: y = √x² is equivalent to y = |x|, meaning it always produces a non-negative value. y = x represents a straight line with a positive slope, which only holds true for non-negative values of x in the context of y = √x².
-
Q: Can y = √x² be differentiated? A: The function is differentiable everywhere except at x=0. The derivative is 1 for x>0 and -1 for x<0.
-
Q: What are some real-world applications of y = √x²? A: Calculating distances, determining the magnitude of vectors (speed, force), and error correction in various applications.
-
Q: Is y = √x² an injective function? A: No, it is not injective (one-to-one) because multiple x-values can produce the same y-value (e.g., x = 2 and x = -2 both result in y = 2).
-
Q: How does y = √x² relate to other mathematical functions? A: It's directly linked to the absolute value function and indirectly to other functions that involve distance calculations or magnitudes.
Conclusion: A Deeper Appreciation of a Fundamental Equation
The seemingly simple equation y = √x² reveals a rich tapestry of mathematical concepts, highlighting the importance of understanding the nuances of square roots and absolute values. Its graphical representation, its connection to the absolute value function, and its applications in various fields underscore its significance. This exploration should provide a clearer and more comprehensive understanding of this fundamental mathematical relationship, equipping you with the knowledge to approach similar equations with greater confidence and insight. Remember the key takeaway: y = √x² is not simply x; it's the absolute value of x, representing a crucial concept in many areas of mathematics and beyond.
Latest Posts
Latest Posts
-
Whats The Square Root Of 250
Aug 26, 2025
-
12 Out Of 30 Is What Percent
Aug 26, 2025
-
What Is The Ka Reaction Of Hcn
Aug 26, 2025
-
Which Is Not A Component Of A Nucleotide
Aug 26, 2025
-
How To Find The Displacement From A Velocity Time Graph
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about Y Square Root Of X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.