24 Is 40 Of What Number
faraar
Sep 21, 2025 · 5 min read
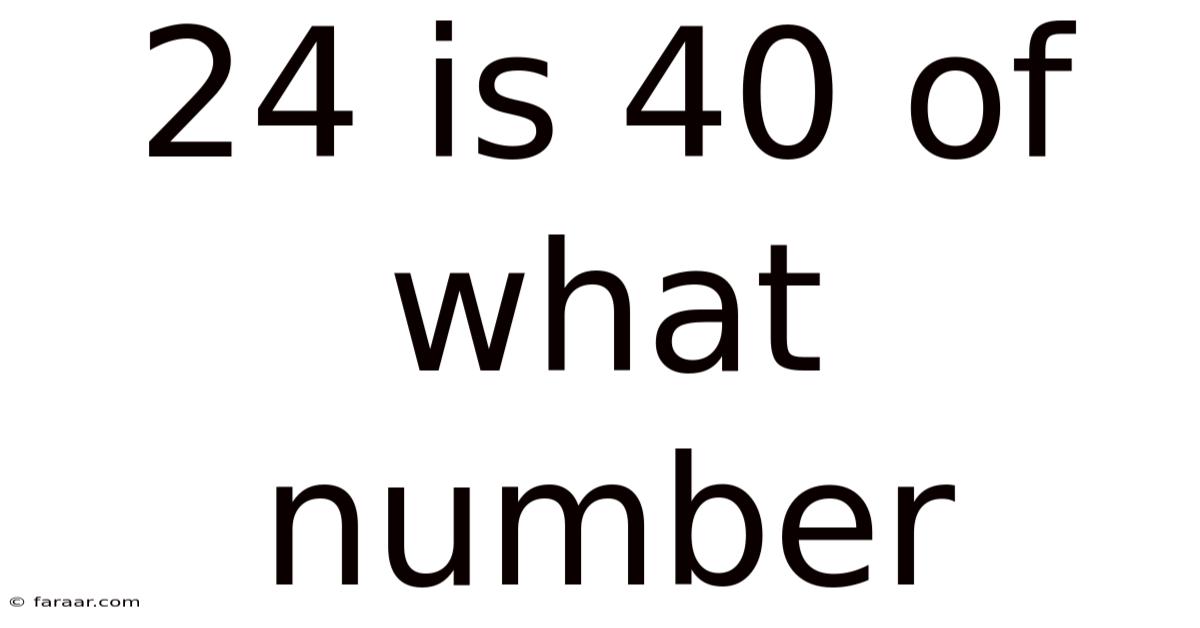
Table of Contents
24 is 40% of What Number? Unlocking the Power of Percentages
Understanding percentages is a fundamental skill in math, crucial for everyday life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will delve into how to solve the problem "24 is 40% of what number?", explaining the process step-by-step, exploring different solution methods, and providing further insights into percentage calculations. We'll also touch upon real-world applications and address frequently asked questions. By the end, you'll not only know the answer but also possess a deeper understanding of percentages and their practical use.
Understanding the Problem
The question "24 is 40% of what number?" is essentially asking us to find the original whole number from which 40% represents 24. This involves working backward from a percentage to the original value. This type of problem is frequently encountered in various scenarios, including:
- Sales and discounts: Determining the original price of an item after a discount is applied.
- Financial calculations: Calculating the principal amount of a loan based on interest payments.
- Data analysis: Interpreting percentages in statistical data to understand the original quantities.
- Scientific measurements: Determining the original quantity from a percentage measurement.
Method 1: Using Proportions
This method leverages the concept of proportions, which states that two ratios are equal. We can set up a proportion to represent the problem:
- 24/x = 40/100
Where:
- 24 represents the part (40% of the unknown number).
- x represents the whole (the unknown number we are trying to find).
- 40/100 represents the percentage (40% expressed as a fraction).
To solve for x, we cross-multiply:
- 24 * 100 = 40 * x
- 2400 = 40x
Then, divide both sides by 40:
- x = 2400 / 40
- x = 60
Therefore, 24 is 40% of 60.
Method 2: Using the Percentage Formula
The basic percentage formula is:
- Part = Percentage × Whole
In our case:
- Part = 24
- Percentage = 40% = 0.40 (Remember to convert the percentage to a decimal by dividing by 100)
- Whole = x (the unknown number)
Substituting these values into the formula, we get:
- 24 = 0.40 * x
To solve for x, divide both sides by 0.40:
- x = 24 / 0.40
- x = 60
Again, we find that 24 is 40% of 60.
Method 3: Working Backwards from the Percentage
This method involves understanding that 40% represents 24. We can then determine what 1% represents and subsequently calculate the whole (100%).
-
Find the value of 1%: If 40% is 24, then 1% is 24 / 40 = 0.6
-
Find the value of 100%: Since 1% is 0.6, then 100% (the whole) is 0.6 * 100 = 60
Therefore, 24 is 40% of 60.
A Deeper Dive into Percentages: Understanding the Concept
Percentages are simply fractions expressed as parts of 100. The word "percent" literally means "out of 100" ( per centum in Latin). Therefore, 40% can be written as 40/100, or its decimal equivalent, 0.40. Understanding this fundamental concept is key to mastering percentage calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is vital in numerous real-world scenarios. Consider these examples:
-
Sales and discounts: A store offers a 20% discount on a $100 item. To calculate the discount amount, you would multiply $100 by 0.20, resulting in a $20 discount. The final price would be $80.
-
Taxes: Sales tax is usually expressed as a percentage. If the sales tax is 6%, and you buy an item for $50, you would calculate the tax amount by multiplying $50 by 0.06, which is $3. The total cost would be $53.
-
Interest rates: Interest on loans and investments is often expressed as a percentage. Understanding interest rate calculations is essential for managing personal finances.
-
Data analysis: Percentages are frequently used to represent data proportions in graphs, charts, and reports. This allows for easier comparison and interpretation of information.
-
Scientific measurements and experiments: In scientific contexts, percentages are used to express concentrations, error rates, and other quantitative data.
Frequently Asked Questions (FAQ)
Q1: What if the percentage is greater than 100%?
A1: A percentage greater than 100% signifies that the "part" is larger than the "whole." This is often encountered when comparing changes over time or when dealing with growth rates. For example, if a company's sales increased by 120%, it means its sales are now 220% of their original value (100% + 120%).
Q2: How do I convert a decimal to a percentage?
A2: To convert a decimal to a percentage, multiply the decimal by 100 and add the % symbol. For example, 0.75 becomes 75% (0.75 * 100 = 75).
Q3: How do I convert a fraction to a percentage?
A3: To convert a fraction to a percentage, first convert the fraction to a decimal by dividing the numerator by the denominator. Then, multiply the decimal by 100 and add the % symbol. For example, 3/4 = 0.75, which converts to 75%.
Q4: Are there any online calculators that can help with percentage calculations?
A4: Yes, many online calculators are available that can perform percentage calculations quickly and accurately. Simply search for "percentage calculator" on a search engine.
Conclusion
Solving the problem "24 is 40% of what number?" demonstrates a fundamental skill in mathematics: understanding and manipulating percentages. We've explored three different methods—using proportions, the percentage formula, and working backwards—all leading to the same answer: 60. This skill is invaluable in various aspects of life, from personal finance to data interpretation and scientific analysis. By understanding the underlying principles and mastering different solution methods, you can confidently tackle similar percentage problems and enhance your quantitative reasoning abilities. Remember, practice is key; the more you work with percentage calculations, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
Ap English Language And Composition Tutor
Sep 21, 2025
-
Potassium Hydroxide Sulfuric Acid Balanced Equation
Sep 21, 2025
-
Kinetic Energy And Mass Are Proportional
Sep 21, 2025
-
Twice The Sum Of 15 And A Number
Sep 21, 2025
-
Drag The Numbers To Order Them From Least To Greatest
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 24 Is 40 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.