Twice The Sum Of 15 And A Number
faraar
Sep 21, 2025 · 6 min read
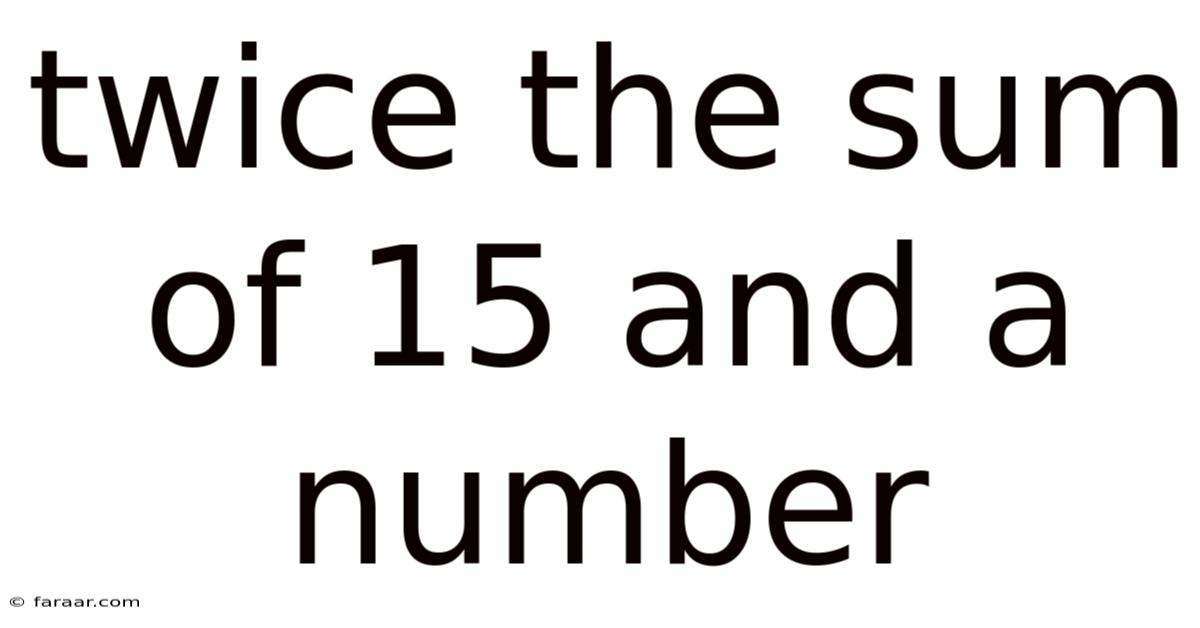
Table of Contents
Twice the Sum of 15 and a Number: A Deep Dive into Mathematical Expressions
This article explores the mathematical expression "twice the sum of 15 and a number," breaking down its meaning, showing how to represent it algebraically, solving related problems, and exploring its applications in various mathematical contexts. Understanding this seemingly simple phrase opens the door to grasping more complex algebraic concepts and problem-solving strategies. We'll cover everything from basic arithmetic to more advanced applications, making this a comprehensive guide for students and anyone interested in improving their mathematical skills.
Introduction: Understanding the Language of Math
Mathematical expressions, like "twice the sum of 15 and a number," are essentially instructions written in the language of mathematics. Deciphering these instructions requires careful attention to the keywords and their order. Let's break down this specific phrase step-by-step:
- "a number": This represents an unknown value, which we typically represent with a variable, most commonly 'x' or 'n'.
- "15 and a number": This indicates the addition of 15 and the unknown number (15 + x).
- "the sum of 15 and a number": This refers to the result of the addition (15 + x).
- "twice the sum of 15 and a number": This means multiplying the sum (15 + x) by 2, resulting in the expression 2(15 + x).
Representing the Expression Algebraically
The phrase "twice the sum of 15 and a number" can be accurately represented using algebraic notation as: 2(15 + x), or equivalently 2(15 + n), where 'x' or 'n' represents the unknown number. The parentheses are crucial; they signify that the addition within the parentheses must be performed before the multiplication by 2. This is due to the order of operations (PEMDAS/BODMAS), where parentheses/brackets take precedence.
Solving Problems Involving the Expression
Let's now explore how to solve problems involving this expression. The difficulty of the problem depends on whether the final result or the unknown number ('x') is given.
Scenario 1: Finding the Expression's Value Given 'x'
Let's say the unknown number, x, is 5. Substituting this value into our algebraic expression:
2(15 + x) = 2(15 + 5) = 2(20) = 40
Therefore, if x = 5, "twice the sum of 15 and the number" equals 40.
Scenario 2: Finding 'x' Given the Expression's Value
This scenario involves solving an algebraic equation. Let's say "twice the sum of 15 and a number" is equal to 50. We set up the equation:
2(15 + x) = 50
Now, we solve for 'x':
- Divide both sides by 2: 15 + x = 25
- Subtract 15 from both sides: x = 10
Therefore, if "twice the sum of 15 and a number" is 50, then the number (x) is 10.
Expanding the Expression and Simplifying
We can also expand the expression 2(15 + x) using the distributive property:
2(15 + x) = 2 * 15 + 2 * x = 30 + 2x
This simplified form, 30 + 2x, is equivalent to the original expression and can be equally useful in solving problems.
Practical Applications and Real-World Examples
While seemingly abstract, this mathematical expression finds practical applications in various real-world scenarios. Here are a few examples:
-
Calculating the total cost of items: Imagine buying 15 apples at $1 each and x oranges at $2 each. The total cost would be 15(1) + x(2) = 15 + 2x. If you double this cost, you have 2(15 + 2x), mirroring the structure of our original expression.
-
Calculating area: Consider a rectangular garden with a length of 15 meters and a width of 'x' meters. The area would be 15x square meters. If you had two identical gardens, the total area would be 2(15x) = 30x, similar to the expression but without the constant addition.
-
Problem solving in everyday life: Many everyday problems can be modeled using similar algebraic expressions. For example, calculating the total earnings after earning a base salary of $15 and commission based on the number of units sold (x).
Advanced Concepts and Extensions
The core concept of "twice the sum of 15 and a number" can be extended to incorporate more complex mathematical concepts:
-
Inequalities: Instead of an equation, we could consider an inequality, such as "twice the sum of 15 and a number is greater than 50." This would be written as 2(15 + x) > 50, and solving for 'x' would yield a range of possible values rather than a single value.
-
Functions: This expression can be defined as a function, f(x) = 2(15 + x). This allows us to input different values for 'x' and obtain corresponding output values. Graphing this function reveals a linear relationship between 'x' and f(x).
-
Systems of Equations: The expression could be part of a system of equations, where it would be combined with other equations to solve for multiple unknowns simultaneously.
Frequently Asked Questions (FAQ)
Q1: Why are the parentheses important in the expression 2(15 + x)?
A1: The parentheses ensure that the addition (15 + x) is performed before the multiplication by 2, according to the order of operations. Without the parentheses, the expression would be interpreted differently, leading to an incorrect result.
Q2: Can I use a different variable instead of 'x'?
A2: Absolutely! You can use any letter or symbol to represent the unknown number, as long as you are consistent throughout your calculations. Common choices include 'n', 'y', or even a descriptive variable like 'apples' if the context allows.
Q3: What if the expression was "twice the difference of 15 and a number"?
A3: In that case, the expression would change to 2(15 - x), reflecting the subtraction instead of addition. The solution process would remain similar, but the outcome would differ.
Q4: How does this relate to other algebraic concepts?
A4: This expression forms the foundation for understanding more complex algebraic concepts, including linear equations, inequalities, functions, and systems of equations. Mastering this basic expression is crucial for building a strong foundation in algebra.
Conclusion: Mastering the Fundamentals
Understanding the mathematical expression "twice the sum of 15 and a number" is not just about solving a single equation. It's about grasping the fundamental principles of algebraic notation, order of operations, and problem-solving strategies. By breaking down the phrase step-by-step, translating it into algebraic notation, and solving various problem types, you solidify your understanding of these fundamental concepts. This knowledge serves as a springboard to tackle more advanced mathematical challenges and successfully apply these principles to various real-world situations. Remember, the key is practice! The more problems you solve, the more confident and proficient you will become in manipulating and understanding algebraic expressions.
Latest Posts
Latest Posts
-
Using Graphing What Is The Approximate Solution Of This Equation
Sep 21, 2025
-
Which Of The Following Has A Nonpolar Covalent Bond
Sep 21, 2025
-
Does A Rhombus Have Opposite Sides That Are Parallel
Sep 21, 2025
-
Find The Value Of A And B
Sep 21, 2025
-
Greatest Common Factor 12 And 16
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Twice The Sum Of 15 And A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.