2/3 Of A Cup Times 3
faraar
Sep 10, 2025 · 5 min read
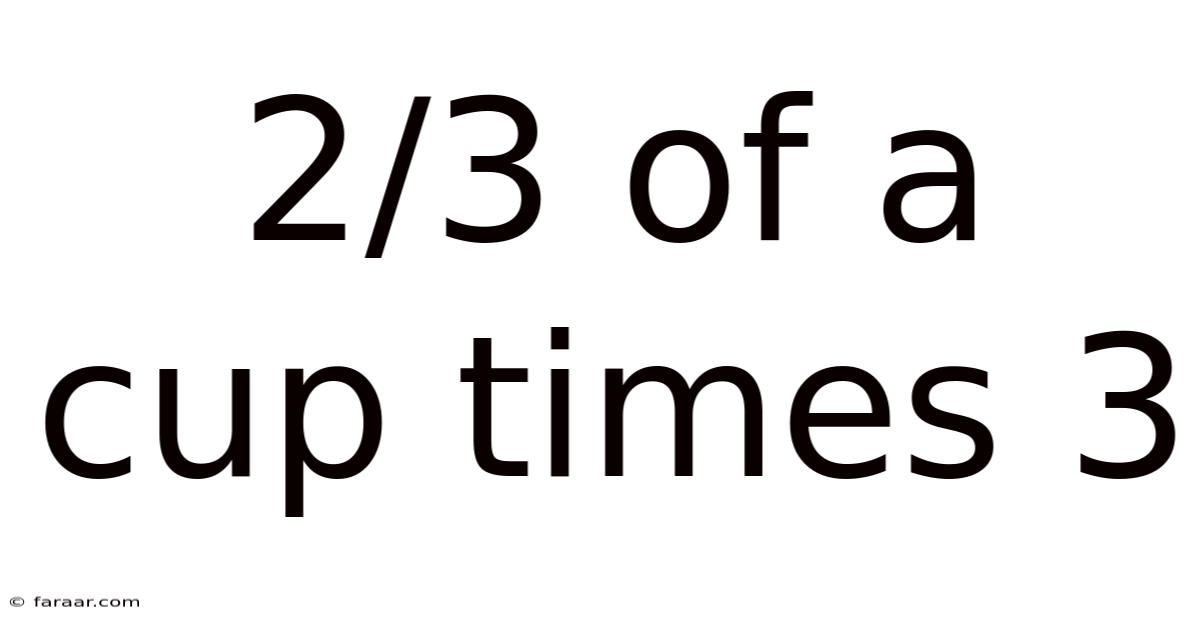
Table of Contents
Decoding the Culinary Conundrum: 2/3 of a Cup Times 3
Have you ever found yourself staring at a recipe, bewildered by the fractional measurements? Many baking and cooking recipes rely on precise ingredient ratios, and understanding how to work with fractions is crucial for achieving the desired outcome. This article delves into the seemingly simple, yet surprisingly revealing, calculation of 2/3 of a cup times 3, exploring its mathematical basis, practical applications in cooking, and extending the concept to broader mathematical principles. We'll unravel the mystery behind this fraction multiplication and empower you to confidently tackle any similar culinary challenges.
Understanding the Basics: Fractions and Multiplication
Before diving into the specific problem, let's refresh our understanding of fractions and multiplication. A fraction represents a part of a whole. It's composed of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many parts make up the whole.
Multiplying fractions is relatively straightforward. You multiply the numerators together to get the new numerator, and you multiply the denominators together to get the new denominator. For example:
1/2 * 1/4 = (1 * 1) / (2 * 4) = 1/8
This basic principle forms the foundation for solving "2/3 of a cup times 3".
Solving the Problem: 2/3 of a Cup Times 3
The phrase "2/3 of a cup times 3" can be interpreted mathematically as:
(2/3) * 3
Following the rules of fraction multiplication:
(2/3) * (3/1) = (2 * 3) / (3 * 1) = 6/3
Now, we simplify the resulting fraction. Since 6 is divisible by 3, we can reduce the fraction:
6/3 = 2
Therefore, 2/3 of a cup times 3 equals 2 cups.
Practical Applications in Cooking and Baking
This seemingly simple calculation has significant implications in the kitchen. Imagine you're baking a cake that requires 2/3 cup of sugar per serving, and you want to triple the recipe. Instead of tediously calculating 2/3 + 2/3 + 2/3, you can directly multiply 2/3 by 3, saving time and ensuring accuracy. This principle applies to countless recipes, from adjusting pancake batter to scaling up a delicious soup. Precise measurements are crucial for achieving consistent results in culinary arts. A slight deviation in ingredient ratios could dramatically alter the final product's taste, texture, and even its ability to rise properly (in the case of baking).
Beyond the Kitchen: Expanding the Mathematical Concept
The calculation (2/3) * 3 = 2 demonstrates a fundamental property of multiplication with fractions: when a fraction is multiplied by its denominator, the result simplifies to its numerator. This holds true for any fraction:
(a/b) * b = a
This property highlights the interconnectedness of various mathematical concepts. It illustrates how fractions, multiplication, and simplification are all interwoven and rely on each other. Understanding this relationship allows for more efficient problem-solving and a deeper understanding of the underlying mathematical principles. Moreover, this concept extends beyond simple fraction multiplication; it forms the basis for understanding more advanced mathematical operations involving fractions, such as solving equations and working with algebraic expressions.
Visualizing the Concept: A Practical Demonstration
Imagine you have a measuring cup divided into thirds. Two-thirds of the cup is filled with flour. If you repeat this process three times – filling the measuring cup to two-thirds three times – you will essentially have filled two complete measuring cups with flour. This visual representation underscores the result of our calculation: 2/3 cup * 3 = 2 cups. This method provides a concrete example, especially helpful for those who find abstract mathematical concepts challenging to grasp. It bridges the gap between theoretical mathematical knowledge and practical, real-world applications. This visual approach is often employed in early mathematics education to aid students in understanding complex ideas.
Addressing Potential Confusion: Common Misconceptions
One common misunderstanding when working with fractions is the temptation to simply add the numerators and denominators. This is incorrect. In our example, some might mistakenly try to add 2 + 3 and 3 + 1, which would lead to an erroneous result of 5/4. It's crucial to remember the correct procedure: multiply the numerators and multiply the denominators separately.
Another potential pitfall involves the improper simplification of fractions. If, after multiplying the fractions, the resulting fraction is not in its simplest form (meaning the numerator and denominator share a common divisor greater than 1), you must reduce the fraction to its lowest terms. Failure to do so could lead to inaccurate measurements in culinary applications.
Frequently Asked Questions (FAQ)
Q: What if the recipe calls for 2/3 cup of a different ingredient?
A: The principle remains the same. Regardless of the ingredient, if you multiply 2/3 of a cup by 3, the result will always be 2 cups. The type of ingredient doesn't change the mathematical calculation.
Q: Can this calculation be applied to other units of measurement?
A: Absolutely! This principle applies to any unit of measurement where fractional values are used, such as milliliters, grams, or even inches. The mathematical process remains identical.
Q: What if I need to adjust the recipe by a different factor, say 5 instead of 3?
A: You would simply replace the '3' in the equation with '5'. (2/3) * 5 = 10/3 which simplifies to 3 1/3 cups. This demonstrates the versatility of the underlying mathematical principle.
Q: How can I easily calculate similar fraction multiplications?
A: Practice makes perfect. The more you work with fractions, the more comfortable you will become with the calculations. Utilizing online calculators or educational websites can also prove beneficial, particularly for more complex fraction multiplications. A strong understanding of the fundamentals is key to mastering these mathematical concepts.
Conclusion: Mastering Fractions for Culinary Success
Mastering fraction multiplication is a critical skill, not just for the mathematically inclined, but for anyone who enjoys cooking and baking. Understanding how to work with fractions empowers you to confidently adjust recipes, ensuring accurate ingredient ratios and consistent, delicious results. The seemingly simple calculation of 2/3 of a cup times 3 – resulting in 2 cups – is more than just a numerical answer; it's a gateway to understanding fundamental mathematical principles and their real-world applications. This knowledge extends beyond the kitchen, contributing to a broader appreciation of mathematical concepts and problem-solving strategies. By grasping these principles, you can tackle culinary challenges with confidence and precision, transforming your cooking experience.
Latest Posts
Latest Posts
-
How Do You Find The Equation Of A Parallel Line
Sep 10, 2025
-
What Is The Volume Of This Solid
Sep 10, 2025
-
What Is 1 4 Divided By 3 As A Fraction
Sep 10, 2025
-
How To Find The Growth Factor
Sep 10, 2025
-
Is Baking Soda A Compound Or An Element
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 2/3 Of A Cup Times 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.