What Is 1/4 Divided By 3 As A Fraction
faraar
Sep 10, 2025 · 5 min read
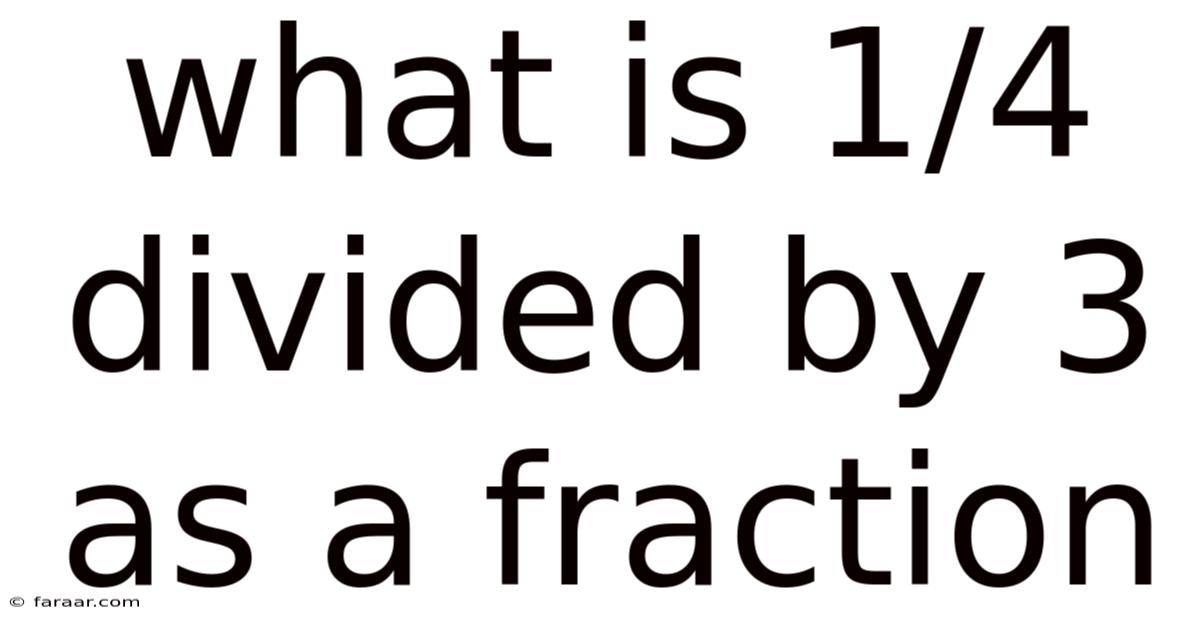
Table of Contents
What is 1/4 Divided by 3 as a Fraction? A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This article will guide you through the steps of solving 1/4 divided by 3, explaining the underlying principles in a way that's easy to grasp, regardless of your mathematical background. We'll delve into the method, explore the underlying mathematical concepts, and answer some frequently asked questions to solidify your understanding of fraction division.
Understanding Fraction Division: The "Keep, Change, Flip" Method
Before diving into the specific problem of 1/4 divided by 3, let's establish a fundamental understanding of fraction division. The most common and efficient method is often referred to as "keep, change, flip" or "keep, switch, flip". This method simplifies the process of dividing fractions into a series of straightforward steps:
-
Keep: Keep the first fraction exactly as it is. In our case, this remains 1/4.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip (or find the reciprocal of) the second fraction. Since 3 can be written as 3/1, flipping it gives us 1/3.
Therefore, the problem 1/4 ÷ 3 transforms into 1/4 × 1/3.
Step-by-Step Calculation: 1/4 ÷ 3
Now, let's apply the "keep, change, flip" method to solve 1/4 divided by 3:
-
Keep: We keep the first fraction as 1/4.
-
Change: We change the division sign (÷) to a multiplication sign (×).
-
Flip: We flip the second fraction, 3 (or 3/1), to its reciprocal, 1/3.
This gives us the new equation: 1/4 × 1/3
-
Multiply the numerators: Multiply the numerators (the top numbers) together: 1 × 1 = 1
-
Multiply the denominators: Multiply the denominators (the bottom numbers) together: 4 × 3 = 12
Therefore, the final answer is 1/12.
Visual Representation: Understanding the Division
Let's visualize this division to further enhance your understanding. Imagine you have a pizza cut into four equal slices (1/4 of a pizza). You want to divide this 1/4 slice among three people equally. To do this, you would need to divide each of the four original slices into three smaller, equal parts. This results in a total of 12 smaller slices (4 x 3 = 12). Each person would then receive one of these 12 smaller slices, representing 1/12 of the original pizza.
This visual representation reinforces the mathematical concept: dividing by 3 essentially means dividing each part into three equal pieces, increasing the total number of parts accordingly.
The Mathematical Principle Behind Fraction Division
The "keep, change, flip" method isn't just a trick; it's a direct consequence of the mathematical definition of division. Division is essentially the inverse operation of multiplication. When you divide a fraction by another fraction (let's say a/b ÷ c/d), you're essentially asking: "What fraction, when multiplied by c/d, will give you a/b?"
The solution involves multiplying a/b by the reciprocal of c/d (d/c). This is because multiplying by the reciprocal "undoes" the multiplication by the original fraction.
Mathematically, we can represent this as:
(a/b) ÷ (c/d) = (a/b) × (d/c) = (a × d) / (b × c)
Applying this to our problem, 1/4 ÷ 3/1, we get:
(1/4) × (1/3) = (1 × 1) / (4 × 3) = 1/12
Decimal Equivalent: Converting the Fraction to a Decimal
While the fraction 1/12 is the precise answer, you might sometimes need the decimal equivalent. To convert 1/12 to a decimal, simply divide the numerator (1) by the denominator (12):
1 ÷ 12 = 0.083333... (the 3 repeats infinitely)
This decimal representation is approximately 0.0833.
Dealing with More Complex Fraction Divisions
The "keep, change, flip" method applies to all fraction divisions, even those involving mixed numbers (numbers with a whole part and a fraction part). Before applying the method to mixed numbers, convert them to improper fractions (where the numerator is larger than the denominator). For example, to divide 2 1/2 by 1/3, first convert 2 1/2 to 5/2, then apply the "keep, change, flip" method.
Frequently Asked Questions (FAQ)
Q1: Why does the "keep, change, flip" method work?
A1: The method is a shortcut derived from the mathematical definition of division as the inverse of multiplication. Multiplying by the reciprocal effectively "undoes" the division.
Q2: Can I divide a fraction by a whole number in a different way?
A2: Yes, you can. You could also multiply the denominator of the fraction by the whole number. For example, 1/4 ÷ 3 is the same as 1/(4 x 3) = 1/12. However, the "keep, change, flip" method is generally considered more efficient and versatile.
Q3: What if I have a mixed number divided by a fraction?
A3: Convert the mixed number into an improper fraction first. Then, apply the "keep, change, flip" method.
Q4: What if I divide by zero?
A4: Dividing by zero is undefined in mathematics. It's not a valid operation.
Q5: Are there other methods to divide fractions?
A5: Yes, there are alternative approaches, but the "keep, change, flip" method is generally the most efficient and widely taught.
Conclusion
Dividing fractions, even seemingly simple ones like 1/4 ÷ 3, involves a fundamental understanding of the relationship between division and multiplication. The "keep, change, flip" method simplifies the process, making it accessible and manageable. By grasping the underlying mathematical principles and practicing the steps, you'll build confidence and proficiency in handling fraction division and other mathematical operations with fractions. Remember, practice makes perfect! Work through several examples, and you’ll quickly master this important mathematical skill. Don't hesitate to review the steps and the visual representation to solidify your understanding. With consistent effort, you'll find that fraction division becomes a straightforward and easily manageable task.
Latest Posts
Latest Posts
-
How Much Is 3 3 4 Cup
Sep 10, 2025
-
Constantinople Became The Center Of The Byzantine Empire Because
Sep 10, 2025
-
What Type Of Reaction Is Shown Below
Sep 10, 2025
-
What Does Dl Mean In Measurement
Sep 10, 2025
-
Green Light Meaning In The Great Gatsby
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/4 Divided By 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.