15 Of 60 Is What Number
faraar
Sep 22, 2025 · 5 min read
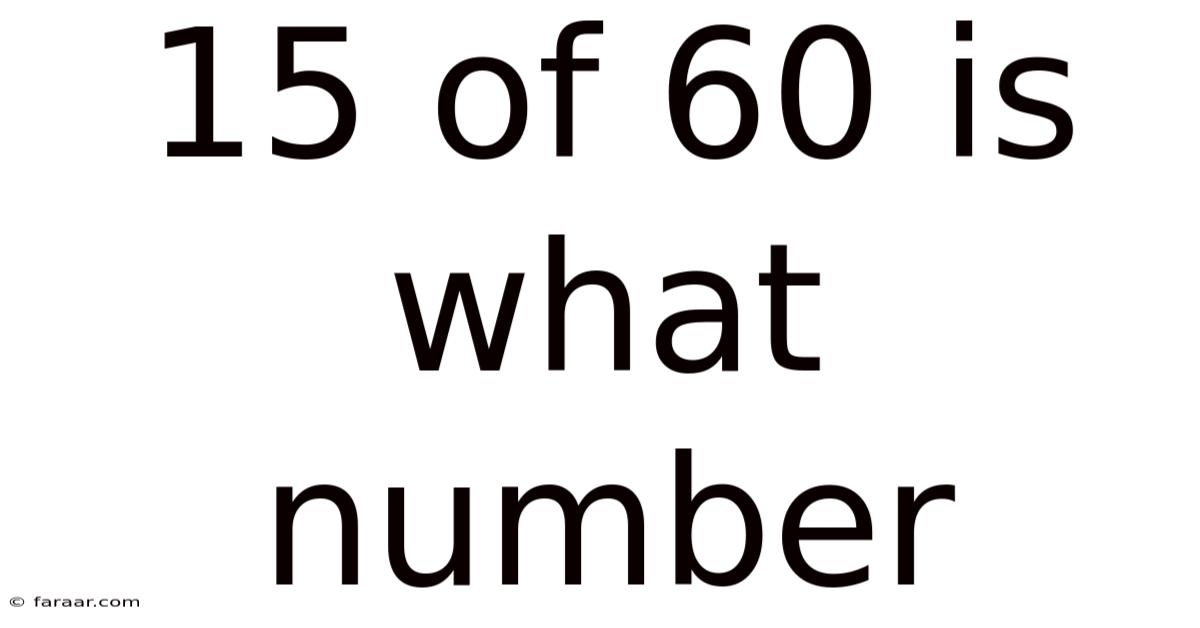
Table of Contents
15 out of 60: Understanding Fractions, Percentages, and Ratios
Knowing how to calculate what 15 out of 60 represents is a fundamental skill in mathematics with applications spanning various fields, from everyday life to advanced scientific calculations. This seemingly simple question opens the door to understanding fractions, percentages, and ratios – core concepts vital for various aspects of life. This article will delve into the calculation, explaining the different approaches and exploring the broader mathematical concepts involved.
Understanding the Problem: Fractions, Percentages, and Ratios
The question "15 out of 60 is what number?" can be interpreted in several ways, leading to different but related answers. We'll explore them all:
- As a Fraction: This represents 15 as a part of a whole of 60. The fraction is written as 15/60.
- As a Percentage: This expresses 15 as a proportion of 60, represented as a number out of 100.
- As a Ratio: This compares the relationship between 15 and 60, often written as 15:60.
All three – fractions, percentages, and ratios – are interconnected and represent different ways of expressing the same proportional relationship.
Method 1: Solving as a Fraction – Simplification and Reduction
The most straightforward approach is to express "15 out of 60" as a fraction: 15/60. This fraction can be simplified by finding the greatest common divisor (GCD) of both the numerator (15) and the denominator (60). The GCD of 15 and 60 is 15.
Dividing both the numerator and the denominator by the GCD:
15 ÷ 15 = 1 60 ÷ 15 = 4
Therefore, 15/60 simplifies to 1/4. This means that 15 is one-quarter of 60.
Method 2: Solving as a Percentage – Converting Fractions to Percentages
To express "15 out of 60" as a percentage, we first represent it as a fraction (15/60), then convert the fraction to a percentage. As we've already established, the simplified fraction is 1/4.
To convert a fraction to a percentage, we multiply the fraction by 100%:
(1/4) * 100% = 25%
Therefore, 15 out of 60 is 25%. This indicates that 15 represents 25% of the total value of 60.
Method 3: Solving as a Ratio – Understanding Proportional Relationships
A ratio expresses the relationship between two quantities. In this case, the ratio is 15:60. Like fractions, ratios can be simplified by dividing both parts by their GCD (which is 15).
15 ÷ 15 = 1 60 ÷ 15 = 4
The simplified ratio is 1:4. This signifies that for every one unit of the first quantity, there are four units of the second quantity. This ratio is equivalent to the fraction 1/4 and the percentage 25%.
The Interplay of Fractions, Percentages, and Ratios
The three methods demonstrate the inherent connection between fractions, percentages, and ratios. They all represent the same proportional relationship. Understanding this connection is crucial for problem-solving in various contexts.
- Fractions provide a precise mathematical representation of parts of a whole.
- Percentages offer a convenient way to express proportions relative to 100, making comparisons easier.
- Ratios highlight the comparative relationship between two or more quantities.
Real-World Applications
The ability to calculate "15 out of 60" has numerous real-world applications:
- Academic Performance: If a student answered 15 questions correctly out of a total of 60, their score would be 25%.
- Sales and Marketing: If a company sold 15 products out of a total stock of 60, their sales performance could be analyzed as a 25% sales rate.
- Financial Analysis: Financial statements often use ratios and percentages to analyze financial health and performance.
- Surveys and Polling: Survey results are often presented as percentages or ratios to show the distribution of opinions or preferences.
- Everyday Calculations: Dividing a pizza, sharing sweets, or calculating discounts all involve these fundamental mathematical concepts.
Further Exploration: Proportions and Problem Solving
The ability to solve "15 out of 60 is what number?" is a stepping stone to understanding more complex proportional problems. Proportions establish equivalence between two ratios. For example:
15/60 = x/100
Solving for 'x' (the equivalent value out of 100, or the percentage) involves cross-multiplication:
15 * 100 = 60 * x 1500 = 60x x = 1500/60 x = 25
This method reinforces the percentage calculation shown earlier. Mastering this simple problem sets the stage for tackling more intricate proportional problems encountered in algebra and beyond.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to solve this?
A1: Yes, you can. A calculator can be used to perform the division 15/60 directly, giving you the decimal 0.25. Multiplying this by 100 will give you the percentage (25%).
Q2: What if the numbers were larger?
A2: The same principles apply, even with larger numbers. You would still simplify the fraction by finding the GCD of the numerator and denominator. A calculator can be particularly helpful with larger numbers to streamline calculations.
Q3: What if I have a different "out of" number?
A3: The process remains the same. For example, if you have "10 out of 25," you'd create the fraction 10/25, simplify it (to 2/5), and then convert it to a percentage (40%) or use cross multiplication for proportion solving.
Q4: Are there other ways to represent this relationship?
A4: Yes. You could also use a decimal representation (0.25) or visualize it using a pie chart or bar graph to illustrate the proportion.
Q5: What is the importance of simplifying fractions?
A5: Simplifying fractions makes them easier to understand and work with. It allows for clearer comparisons and easier calculations in subsequent steps.
Conclusion: Building a Strong Foundation in Mathematics
Understanding how to calculate "15 out of 60 is what number?" is not merely about finding the answer (25%). It's about grasping the underlying principles of fractions, percentages, and ratios, which are building blocks for more advanced mathematical concepts. By mastering these fundamental skills, you build a strong foundation for success in mathematics and various real-world applications. Remember the interconnectedness of these concepts—they are all different lenses through which we view the same proportional relationship. Practice various problems using different numbers and scenarios to solidify your understanding and build confidence in your mathematical abilities. This fundamental skill will serve you well throughout your academic and professional life.
Latest Posts
Latest Posts
-
What Expression Is Equivalent To Mc012 1 Jpg
Sep 22, 2025
-
How To Find Secant Line Equation
Sep 22, 2025
-
What Macromolecule Makes Up The Majority Of The Cell Membrane
Sep 22, 2025
-
What Is 5 3 As A Percent
Sep 22, 2025
-
What Advantages Did The Union Have Over The South
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 60 Is What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.