12 Is 3 Of What Number
faraar
Sep 19, 2025 · 5 min read
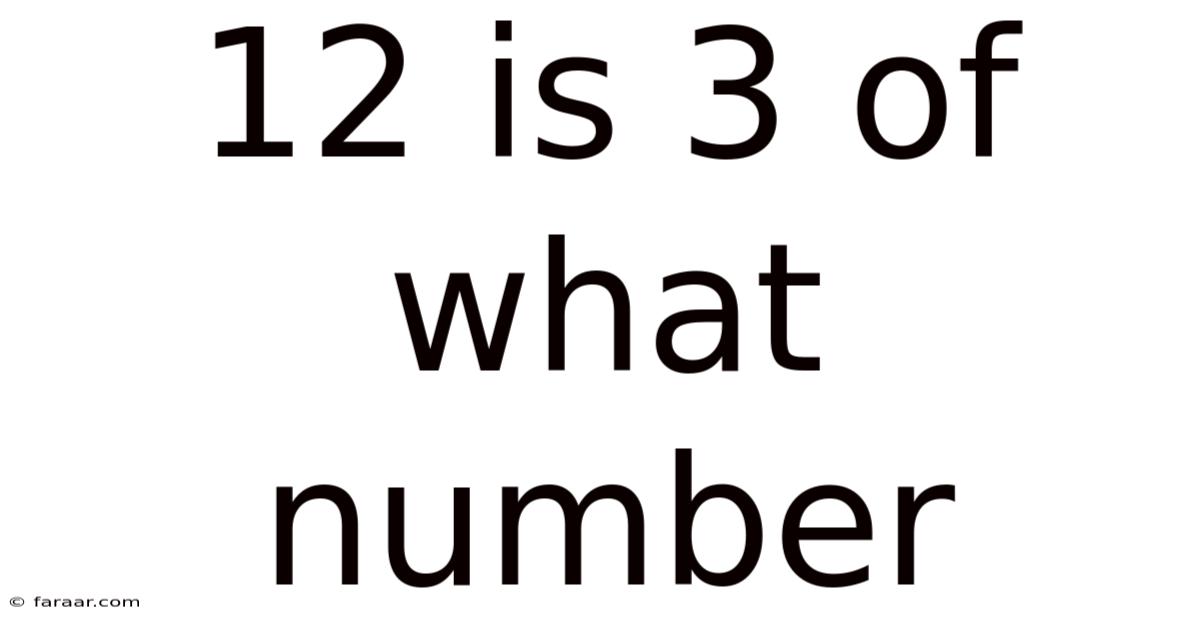
Table of Contents
12 is 3 of What Number? Unlocking the Power of Proportions
This seemingly simple question, "12 is 3 of what number?", opens the door to a fundamental concept in mathematics: proportions. Understanding proportions is crucial not just for solving simple arithmetic problems, but also for tackling complex scenarios in algebra, geometry, and even real-world applications like scaling recipes or calculating percentages. This article will explore various methods to solve this problem, delve into the underlying mathematical principles, and provide a solid foundation for tackling similar proportional reasoning challenges.
Understanding the Problem: A Proportional Relationship
At its core, the question "12 is 3 of what number?" describes a proportional relationship. We can represent this relationship mathematically as a fraction or ratio:
12/x = 3/1
Where:
- 12 represents the given part.
- x represents the unknown whole number.
- 3 represents the known fraction (3 out of 1, or 3/1, which simplifies to 3).
This equation states that 12 is to x as 3 is to 1. The goal is to find the value of 'x'. Let's explore different ways to solve for x.
Method 1: Cross-Multiplication
Cross-multiplication is a classic and efficient method for solving proportions. It involves multiplying the numerator of one fraction by the denominator of the other and vice-versa. Applying this method to our equation:
12/x = 3/1
Cross-multiplying, we get:
12 * 1 = 3 * x
Simplifying:
12 = 3x
Now, we isolate 'x' by dividing both sides of the equation by 3:
x = 12/3
x = 4
Therefore, 12 is 3 of the number 4.
Method 2: Using the Concept of Unit Rate
Another approach involves finding the unit rate. If 3 represents 1/1 (or a whole unit), then we need to find what represents 12. To do this, we divide the given part by the fraction:
12 / (3/1) = 12 * (1/3) = 4
This directly gives us the answer: 4.
This method is particularly useful when dealing with word problems where understanding the unit rate offers valuable insight into the problem. For example, if 3 apples cost $1, how many apples can you buy with $12? The unit rate ($1/3 apples) easily solves this.
Method 3: Scaling Up/Down
This method is intuitive and visually helpful, particularly for beginners. We can visualize this problem as scaling up from 3 to 12. If 3 represents the whole, and we have 12, then we can think about how many times bigger 12 is compared to 3:
12 / 3 = 4
This indicates that 12 is four times larger than 3. If 3 represents the whole (i.e., 3 out of 3, or 1), then to find the total number represented by 12, we scale up our whole by the same factor:
1 * 4 = 4
This confirms our answer: 4.
This method highlights the direct proportional relationship between the parts and the whole.
The Underlying Mathematical Principle: Proportional Reasoning
All three methods are based on the core concept of proportional reasoning. This involves understanding the relationship between two or more quantities where the ratio between them remains constant. In our problem, the ratio of the part to the whole (12:x) is equal to the ratio of the given fraction to its whole (3:1).
Proportional reasoning is a critical skill in various mathematical areas. For example:
- Geometry: Similar triangles and other shapes maintain constant ratios between corresponding sides.
- Algebra: Solving equations often involves manipulating proportions to isolate variables.
- Statistics: Percentages and rates are based on proportional relationships.
- Real-World Applications: Scaling recipes, calculating distances on maps, and understanding economic growth rates all rely on proportional reasoning.
Expanding the Concept: More Complex Proportions
The basic principle of proportions can be extended to more complex problems. For instance:
-
"20 is 5/8 of what number?" We can set up the proportion: 20/x = 5/8. Cross-multiplying yields 160 = 5x, and solving for x gives x = 32.
-
"What is 25% of 80?" This can be written as a proportion: x/80 = 25/100. Solving this gives x = 20.
-
Word Problems: "If a car travels 150 miles in 3 hours, how far will it travel in 5 hours at the same speed?" This involves setting up a proportion: 150 miles/3 hours = x miles/5 hours. Solving for x provides the distance traveled in 5 hours.
Mastering proportional reasoning is about understanding the underlying relationship between quantities and applying appropriate methods to solve for unknown values.
Frequently Asked Questions (FAQ)
Q: Can I use decimals instead of fractions in these calculations?
A: Yes, absolutely. You can convert the fractions to decimals and perform the calculations using decimals. For example, 3/1 is equal to 3.0, so you could use 12/x = 3.0 to solve. The result will be the same.
Q: Are there other ways to solve proportions besides cross-multiplication?
A: Yes, as demonstrated above, unit rate and scaling methods are effective alternatives. The best method depends on the specific problem and your personal preference.
Q: What if the given numbers are not whole numbers?
A: The principles remain the same. You can still use cross-multiplication or other methods to solve for the unknown variable, even if the numbers involved are decimals or fractions.
Q: How can I improve my proportional reasoning skills?
A: Practice is key! Work through various problems of increasing complexity. Focus on understanding the underlying relationship between the quantities involved, and don't be afraid to use different solution methods to find the most efficient approach for each problem.
Conclusion: Mastering Proportions, Mastering Math
The seemingly simple question, "12 is 3 of what number?", serves as an excellent introduction to the fundamental concept of proportions. Understanding proportions is a cornerstone of mathematical proficiency, extending far beyond simple arithmetic problems. By mastering proportional reasoning, you gain a valuable tool for solving a wide range of mathematical and real-world challenges. The methods discussed – cross-multiplication, unit rate, and scaling – offer versatile approaches to tackling proportional problems, empowering you to confidently navigate mathematical scenarios and build a stronger foundation in mathematical understanding. Remember, practice is key to mastering this essential skill. So, continue practicing, explore different problems, and enjoy the journey of unlocking the power of proportions!
Latest Posts
Latest Posts
-
What Does Negative Divided By Positive Equal
Sep 20, 2025
-
Four Points Are Always Coplanar If
Sep 20, 2025
-
Eight Minus The Square Of A Number
Sep 20, 2025
-
Exponential Word Problems Growth And Decay
Sep 20, 2025
-
How To Find The Relative Minimum
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 12 Is 3 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.