Eight Minus The Square Of A Number
faraar
Sep 20, 2025 · 6 min read
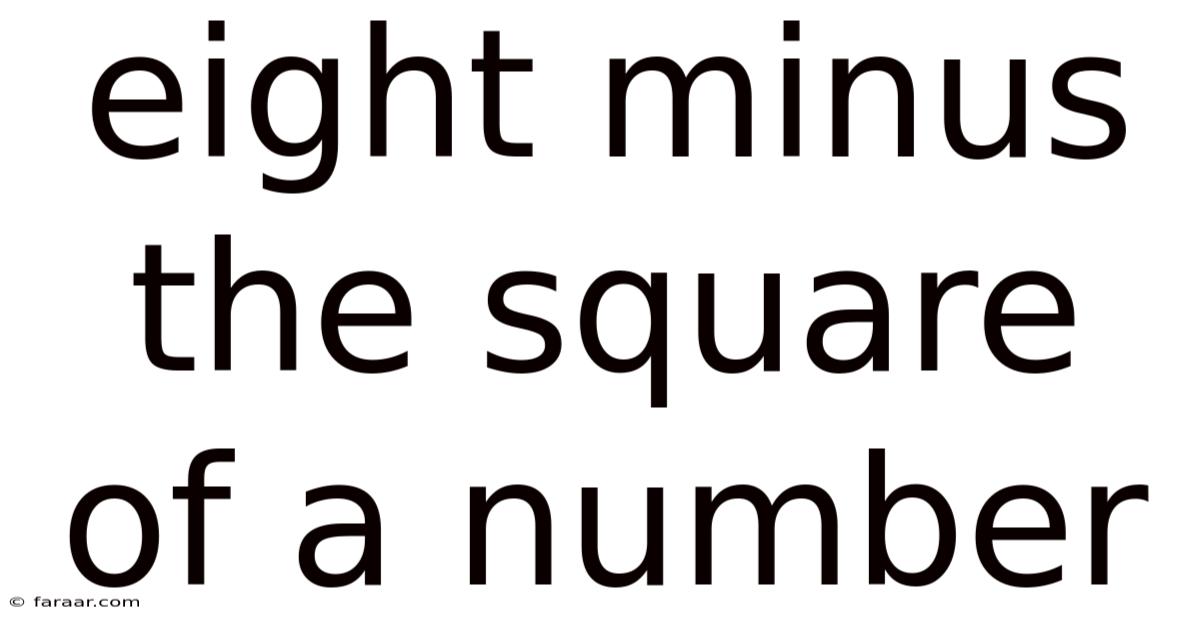
Table of Contents
Unveiling the Mysteries of "Eight Minus the Square of a Number"
Understanding the expression "eight minus the square of a number" might seem deceptively simple at first glance. However, this seemingly straightforward phrase opens a door to a world of mathematical concepts, from basic algebra to the exploration of quadratic equations and their graphical representations. This article delves into the intricacies of this expression, exploring its various interpretations, applications, and the rich mathematical landscape it reveals. We'll cover everything from solving basic equations to understanding its graphical representation, ensuring a comprehensive understanding suitable for learners of all levels.
Understanding the Core Expression
The phrase "eight minus the square of a number" translates directly into a mathematical expression: 8 - x², where 'x' represents the unknown number. This is a simple algebraic expression, combining a constant (8) with a variable (x) raised to the power of two (x²). The core concept is the subtraction of a squared number from eight. The simplicity of the expression belies its potential for complexity when we delve into its applications and solutions.
Solving Equations Involving "Eight Minus the Square of a Number"
The real power of this expression emerges when it's used within an equation. For instance, let's consider the equation: 8 - x² = 0. This equation asks: "What number, when squared and subtracted from eight, results in zero?" To solve this, we can rearrange the equation:
- x² = 8
Taking the square root of both sides, we get:
- x = ±√8
This simplifies to:
- x = ±2√2
This solution reveals two possible values for x: positive 2√2 and negative 2√2. This highlights a key characteristic of quadratic equations: they can often have multiple solutions.
Exploring Different Equation Scenarios
Let's explore other scenarios involving our core expression. Consider the equation: 8 - x² = 3. This time, we're looking for a number whose square, when subtracted from eight, equals three. Solving this:
- 8 - x² = 3
- -x² = 3 - 8
- -x² = -5
- x² = 5
- x = ±√5
Again, we have two solutions: positive √5 and negative √5. This demonstrates that the solutions to equations based on "eight minus the square of a number" are often symmetric around zero.
The Graphical Representation: Parabolas and Their Significance
The expression 8 - x² represents a parabola when graphed on a Cartesian coordinate system. A parabola is a U-shaped curve that's defined by a quadratic equation. To understand the graph, let's consider plotting several points:
- If x = 0, then 8 - x² = 8. This gives us the point (0, 8).
- If x = 1, then 8 - x² = 7. This gives us the point (1, 7).
- If x = 2, then 8 - x² = 4. This gives us the point (2, 4).
- If x = 3, then 8 - x² = -1. This gives us the point (3, -1).
- If x = -1, then 8 - x² = 7. This gives us the point (-1, 7).
- If x = -2, then 8 - x² = 4. This gives us the point (-2, 4).
- If x = -3, then 8 - x² = -1. This gives us the point (-3, -1).
Plotting these points and connecting them reveals an inverted parabola. The parabola's vertex, the highest point, is at (0, 8). The parabola opens downwards, reflecting the negative coefficient of the x² term. This graphical representation provides a visual understanding of the relationship between the input (x) and the output (8 - x²). The graph clearly shows that there are two x-values for every y-value (except for the vertex), illustrating the possibility of multiple solutions we encountered while solving equations.
Real-World Applications
While seemingly abstract, the concept of "eight minus the square of a number" finds applications in various real-world scenarios. These applications often involve modeling situations where a quantity decreases quadratically. For example:
-
Physics: Projectile motion can be modeled using quadratic equations. The height of a projectile over time might be represented by an equation similar to our core expression, where the downward acceleration of gravity contributes to the quadratic term.
-
Engineering: The strength of a certain material might decrease with the square of its age or the square of the stress applied to it. This might be represented using a similar quadratic expression.
-
Economics: In some economic models, the profit margin might decrease quadratically as the production level increases beyond a certain point. This could be represented by a modified version of our expression.
These examples showcase how a seemingly simple mathematical concept can translate to the modeling and understanding of complex real-world phenomena.
Advanced Concepts and Extensions
The exploration of "eight minus the square of a number" can be extended to more advanced mathematical concepts:
-
Calculus: We can use calculus to find the maximum value of the function represented by 8 - x², which corresponds to the vertex of the parabola (at x=0). The derivative of 8 - x² is -2x, and setting this to zero reveals the maximum at x=0.
-
Completing the Square: This technique is vital for solving more complex quadratic equations, especially those that don't easily factor. It involves manipulating the equation to form a perfect square trinomial.
-
The Discriminant: In more complex quadratic equations (ax² + bx + c = 0), the discriminant (b² - 4ac) determines the nature of the solutions. A positive discriminant indicates two real solutions, a zero discriminant indicates one real solution, and a negative discriminant indicates two complex solutions.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 8 - x² and x² - 8?
A: While both involve the square of a number and eight, they represent different mathematical relationships. 8 - x² represents a parabola that opens downwards, while x² - 8 represents a parabola that opens upwards. Their graphs are reflections of each other across the x-axis.
-
Q: Can "eight minus the square of a number" ever be negative?
A: Yes, definitely. If the value of x² is greater than 8, then the expression 8 - x² will result in a negative value.
-
Q: What are the roots of the equation 8 - x² = 0?
A: The roots (or solutions) are x = 2√2 and x = -2√2. These are the x-intercepts of the parabola represented by the equation.
Conclusion
The expression "eight minus the square of a number" serves as a gateway to a deeper understanding of algebra, quadratic equations, and their graphical representations. From solving simple equations to exploring the intricacies of parabolas and their real-world applications, this seemingly simple expression unlocks a wealth of mathematical concepts. This exploration demonstrates the beauty and power of mathematics, where even the simplest concepts can lead to profound insights and practical applications across various disciplines. The ability to manipulate, solve, and visualize this expression is a fundamental step towards mastering more advanced mathematical concepts. By understanding this core idea, you've laid a solid foundation for future explorations in algebra and beyond.
Latest Posts
Latest Posts
-
Is A Square Also A Rhombus
Sep 20, 2025
-
How To Find The Terminal Point On The Unit Circle
Sep 20, 2025
-
What Is 1 3 Cup Doubled In A Recipe
Sep 20, 2025
-
17 5 Rounded To The Nearest Tenth
Sep 20, 2025
-
30 Percent Of What Number Is 12
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Eight Minus The Square Of A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.