1 8 Divided By 2 In Fraction
faraar
Sep 16, 2025 · 6 min read
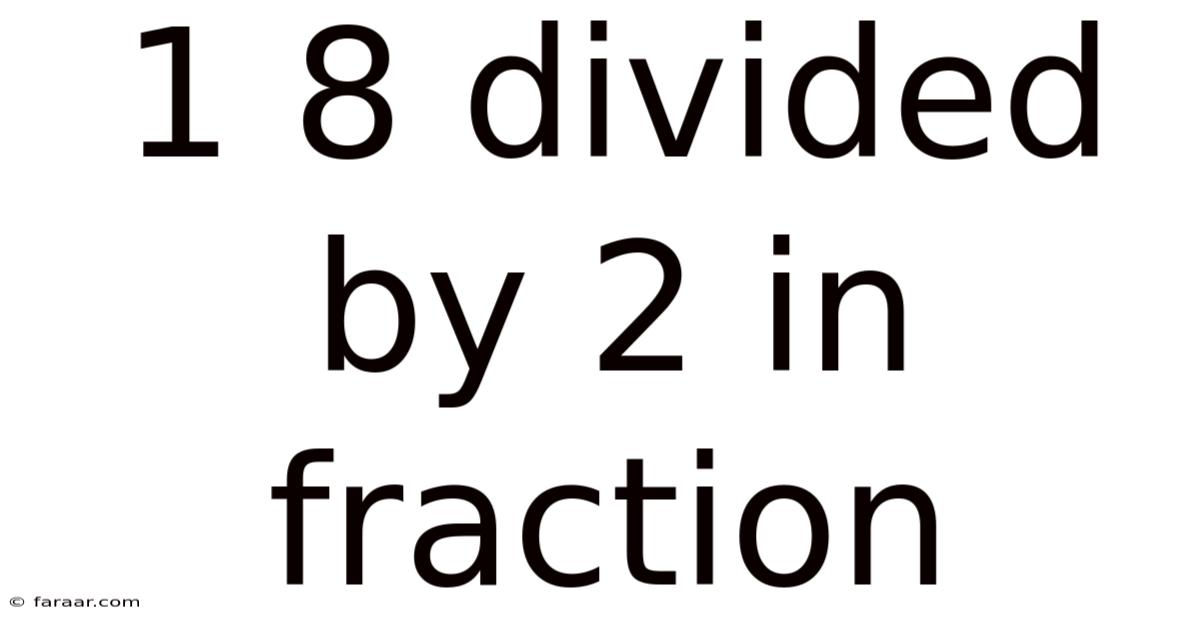
Table of Contents
18 Divided by 2: Understanding Fractions and Division
This article delves into the seemingly simple problem of 18 divided by 2, but expands upon it to explore the fascinating world of fractions and their relationship to division. We'll move beyond simply stating the answer and explore the underlying mathematical concepts, offering a deeper understanding for students and anyone curious about the fundamentals of arithmetic. Understanding this seemingly basic operation lays a crucial foundation for more complex mathematical concepts later on.
Introduction: Fractions, Division, and the Big Picture
The expression "18 divided by 2" can be represented in several ways: 18 ÷ 2, 18/2, or even as a fraction: 18/2. While the answer is straightforward (9), the true value lies in understanding why the answer is 9 and how this relates to the broader concept of fractions. Fractions represent parts of a whole, and division is essentially the process of splitting a whole into equal parts. In this case, we're splitting 18 into 2 equal parts.
Understanding Fractions: Parts of a Whole
A fraction is written in the form a/b, where 'a' is the numerator and 'b' is the denominator. The numerator represents the number of parts we have, and the denominator represents the total number of equal parts that make up the whole. For example, in the fraction 3/4, the numerator (3) indicates we have 3 parts, and the denominator (4) indicates the whole is divided into 4 equal parts.
Division as Sharing Equally: The Concept of "Parts"
Division, at its core, is about equitable distribution or sharing. When we divide 18 by 2, we're asking: "If we have 18 items and we want to divide them equally among 2 groups, how many items will each group receive?" The answer, of course, is 9. Each group gets 9 items. This directly relates to the fraction 18/2, where 18 is the total number of items, and 2 is the number of groups.
18 Divided by 2: A Step-by-Step Approach Using Visual Aids
Let's visualize this with examples:
-
Using Objects: Imagine you have 18 apples. If you want to divide them equally between 2 people, you'd give each person 9 apples. This illustrates the division 18 ÷ 2 = 9.
-
Using a Number Line: A number line can also visually represent this. Start at 0 and make jumps of 2 until you reach 18. Count how many jumps you made—this will be 9 jumps, representing the answer.
-
Using a Diagram: Draw a rectangle and divide it into 18 equal squares. Then, divide the rectangle into two equal halves. You'll find that each half contains 9 squares, again visually demonstrating that 18 ÷ 2 = 9.
Representing 18/2 as a Mixed Number (Though Not Necessary Here)
While 18/2 simplifies directly to 9, it's helpful to understand how improper fractions (where the numerator is larger than the denominator) can be expressed as mixed numbers. An improper fraction represents a value greater than 1. To convert an improper fraction to a mixed number, we perform division.
Let's take an example: 7/2. We divide the numerator (7) by the denominator (2): 7 ÷ 2 = 3 with a remainder of 1. This means the mixed number equivalent is 3 1/2. This signifies 3 whole units and 1/2 of another unit. However, in the case of 18/2, there is no remainder, thus it simplifies directly to a whole number: 9.
The Relationship Between Fractions and Division:
The fraction a/b is mathematically equivalent to the division a ÷ b. This is a fundamental concept in arithmetic. This equivalence allows us to solve problems using either fractions or division, depending on which approach is more convenient.
Solving Similar Problems: Applying the Concept
Let's extend our understanding by solving similar problems:
-
24 divided by 4 (24/4): This represents sharing 24 items equally among 4 groups. The answer is 6.
-
30 divided by 5 (30/5): Sharing 30 items among 5 groups results in 6 items per group.
-
36 divided by 6 (36/6): This results in 6 items per group.
Notice a pattern? These are all examples of simplifying fractions where the numerator is a multiple of the denominator. This leads to a whole number answer.
Extending the Concept to More Complex Fractions:
What if we had a problem that didn't simplify to a whole number? For example, 17/2. This is still the same process. We divide 17 by 2. The result is 8 with a remainder of 1. Therefore, 17/2 is equivalent to 8 1/2, or 8.5 in decimal form.
Simplifying Fractions: A Crucial Step
Simplifying fractions means reducing them to their lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by that GCD. For example, the fraction 12/18 can be simplified. The GCD of 12 and 18 is 6. Dividing both the numerator and denominator by 6 gives us 2/3, the simplified form. This principle is essential for understanding equivalent fractions.
Equivalent Fractions:
Equivalent fractions represent the same value but are written differently. For instance, 1/2, 2/4, 3/6, and so on, are all equivalent fractions. They all represent half of a whole. Understanding equivalent fractions is crucial for comparing and manipulating fractions in more advanced mathematical contexts.
Decimal Representation:
Fractions can also be expressed as decimals. To convert a fraction to a decimal, divide the numerator by the denominator. For instance, 1/2 = 0.5, and 3/4 = 0.75. This decimal representation is often useful for practical applications and calculations.
Fractions in Real-World Applications:
Fractions are not just abstract mathematical concepts; they are used extensively in everyday life:
- Cooking and Baking: Recipes often use fractions (e.g., 1/2 cup of sugar).
- Measurement: We use fractions to measure lengths, weights, and volumes (e.g., 2 1/4 inches).
- Time: Telling time involves fractions (e.g., a quarter past the hour).
- Finance: Percentages, which are essentially fractions (e.g., 50% = 1/2), are fundamental in financial calculations.
Frequently Asked Questions (FAQ)
-
Q: What if the denominator is 0? A: Division by zero is undefined in mathematics. It's an invalid operation.
-
Q: How do I divide larger numbers? A: The same principles apply. You can use long division or a calculator for larger numbers.
-
Q: How can I improve my understanding of fractions? A: Practice regularly, use visual aids, and work through various examples.
Conclusion: Mastering Fractions and Division
Understanding the division of 18 by 2, and indeed the broader concepts of fractions and division, is fundamental to mathematical literacy. It's not just about getting the answer (9); it's about comprehending the underlying principles and how they relate to various aspects of mathematics and real-world scenarios. This understanding forms a bedrock for more complex mathematical concepts learned later in life. By mastering these fundamentals, you open the door to a deeper appreciation and understanding of the world around you, where mathematical principles play an integral role. Through consistent practice and exploration, you can build a solid foundation for future mathematical success.
Latest Posts
Latest Posts
-
How To Say Grandmother In Cantonese
Sep 16, 2025
-
What Percent Of 84 Is 63
Sep 16, 2025
-
Classify Each Reaction As Endothermic Or Exothermic
Sep 16, 2025
-
What Theory Did Fascists Use To Support Their Own Ideology
Sep 16, 2025
-
A Quadrilateral With 2 Right Angles
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1 8 Divided By 2 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.