What Percent Of 84 Is 63
faraar
Sep 16, 2025 · 5 min read
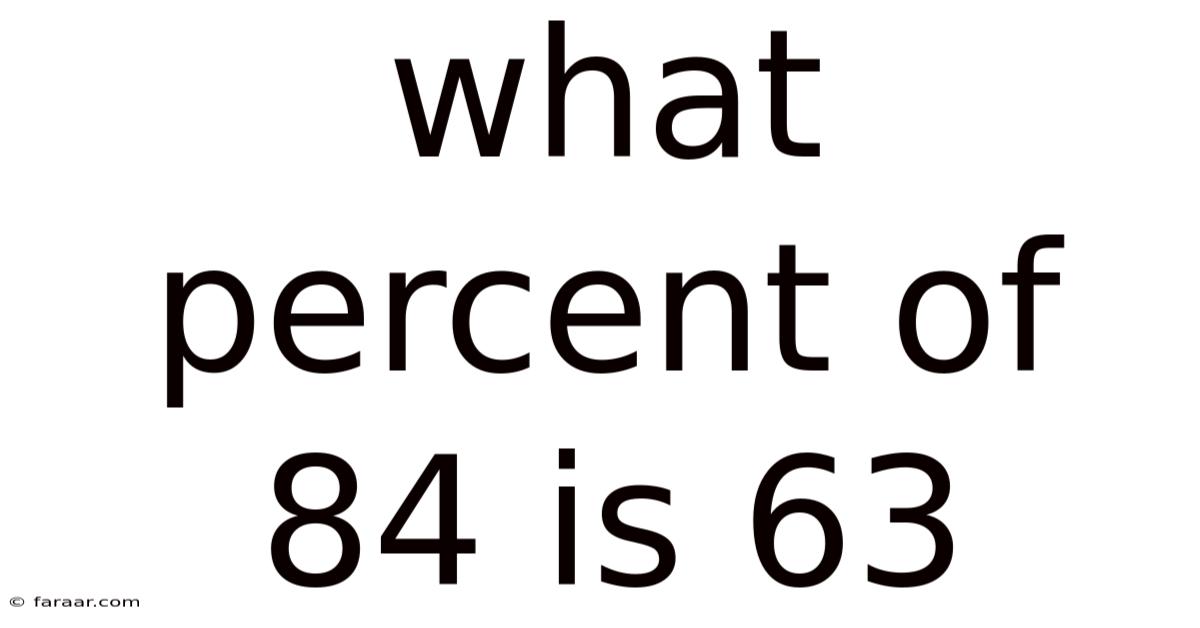
Table of Contents
What Percent of 84 is 63? A Comprehensive Guide to Percentage Calculations
Finding what percent one number represents of another is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and sales tax to understanding statistical data and financial reports. This article provides a comprehensive guide to solving the problem "What percent of 84 is 63?", explaining the steps involved, exploring different methods, and delving into the underlying mathematical principles. We'll also look at related percentage problems and offer some practical applications.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" signifies "percent" or "out of 100". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are incredibly useful because they provide a standardized way to compare proportions and make relative comparisons.
Method 1: Using Proportions
The most straightforward method to solve "What percent of 84 is 63?" is by setting up a proportion. A proportion is an equation that states that two ratios are equal. In this case, we can set up the following proportion:
x/100 = 63/84
Where 'x' represents the percentage we're trying to find. This equation reads: "x out of 100 is equal to 63 out of 84".
To solve for x, we can cross-multiply:
84x = 6300
Now, divide both sides by 84:
x = 6300 / 84
x = 75
Therefore, 63 is 75% of 84.
Method 2: Using Decimal Conversion
Another approach involves converting the fraction 63/84 into a decimal and then multiplying by 100 to express it as a percentage.
First, we simplify the fraction:
63/84 = 3/4 (Both the numerator and denominator are divisible by 21)
Next, we convert the simplified fraction to a decimal by dividing the numerator by the denominator:
3 ÷ 4 = 0.75
Finally, we multiply the decimal by 100 to express it as a percentage:
0.75 × 100 = 75%
Again, we arrive at the answer: 63 is 75% of 84.
Method 3: Using the Percentage Formula
The percentage formula provides a more direct approach. The formula is:
(Part/Whole) x 100 = Percentage
In our problem:
Part = 63 Whole = 84
Substituting these values into the formula:
(63/84) x 100 = Percentage
0.75 x 100 = 75%
Once again, the result is 75%.
Understanding the Calculation: A Deeper Dive
The essence of these calculations lies in the concept of ratios and proportions. We are essentially comparing the part (63) to the whole (84) and expressing this comparison as a fraction of 100 (a percentage). The different methods simply represent alternative ways to manipulate this fundamental relationship. The simplification of the fraction 63/84 to 3/4 highlights the importance of simplifying fractions before performing calculations; it makes the arithmetic simpler and less prone to errors.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world situations. Here are a few examples:
- Sales and Discounts: Calculating the discount amount on a sale item. For instance, a 20% discount on a $100 item means a saving of $20.
- Taxes: Determining the amount of sales tax or income tax owed.
- Tips and Gratuities: Calculating a tip percentage in a restaurant.
- Interest Rates: Understanding interest earned on savings accounts or interest paid on loans.
- Statistical Analysis: Interpreting data presented as percentages in surveys, polls, and research reports. Understanding percentage change is important for tracking trends and growth.
- Financial Statements: Analyzing financial reports that use percentages to represent various ratios and proportions, such as profit margins and debt-to-equity ratios.
- Grade Calculation: Calculating your final grade in a course based on weighted percentages of assignments and exams.
Solving Similar Percentage Problems
The methods described above can be readily applied to other percentage problems. For example:
- What percent of 120 is 30? Using the proportion method: x/100 = 30/120. Solving for x yields 25%.
- What is 15% of 200? Using the percentage formula: (15/100) x 200 = 30.
- 70 is what percent of 140? Using the percentage formula: (70/140) x 100 = 50%.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a percentage increase or decrease? A: Percentage change calculations involve finding the difference between two numbers, dividing by the original number, and then multiplying by 100. The formula is: [(New Value - Old Value) / Old Value] x 100. A positive result indicates an increase, while a negative result indicates a decrease.
-
Q: Can I use a calculator to solve percentage problems? A: Yes, most calculators have a percentage function (%) that simplifies these calculations. However, understanding the underlying principles is still essential.
-
Q: Why is it important to learn how to calculate percentages manually? A: While calculators are helpful, understanding the manual methods improves your mathematical intuition and problem-solving skills. It also helps in situations where a calculator is not readily available.
Conclusion
Calculating percentages is a versatile skill with practical applications in numerous areas of life. Understanding the different methods – using proportions, decimal conversions, and the percentage formula – empowers you to solve a wide range of percentage problems accurately and efficiently. Mastering these techniques not only enhances your mathematical abilities but also equips you to better understand and interpret quantitative information in various contexts. Remember, the core concept involves relating a part to a whole and expressing that relationship as a fraction of 100. By practicing these methods and understanding the underlying principles, you'll become confident and proficient in tackling percentage calculations.
Latest Posts
Latest Posts
-
Equation Of Tangent Line Implicit Differentiation
Sep 17, 2025
-
7 8 Square Foot In 1 4 Hour
Sep 17, 2025
-
A Bromine Isotope With 46 Neutrons
Sep 17, 2025
-
1 Cubic Ft Of Water Weighs
Sep 17, 2025
-
Calculate The Molarity Of The Two Solutions
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 84 Is 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.