1 4 9 16 25 36
faraar
Sep 23, 2025 · 6 min read
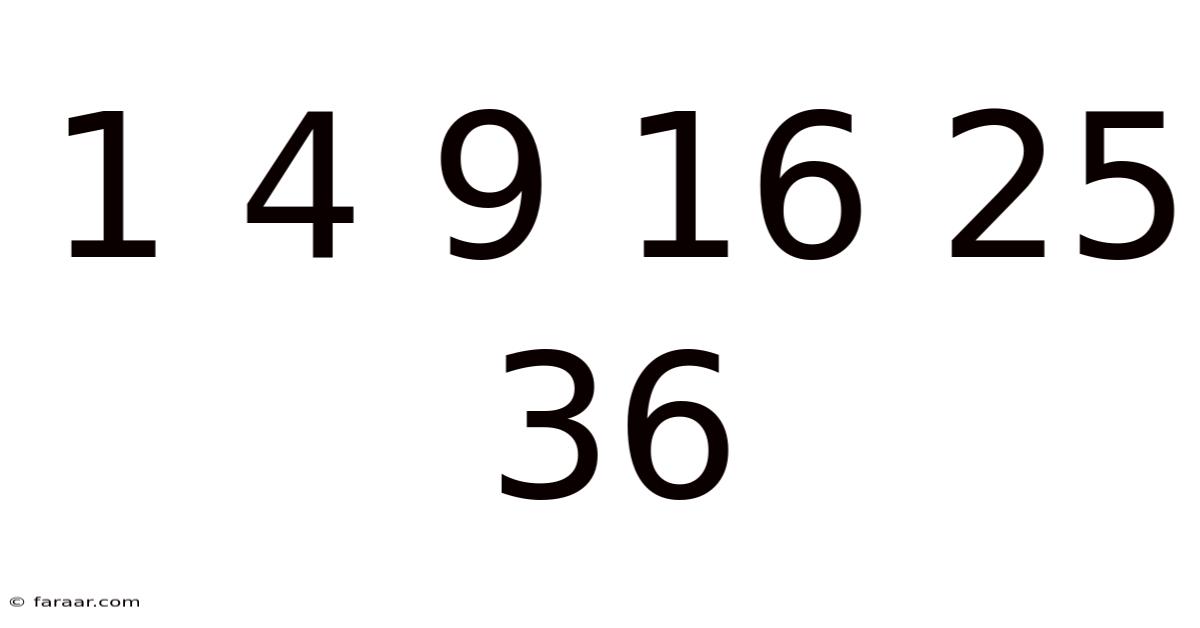
Table of Contents
Unlocking the Secrets of 1, 4, 9, 16, 25, 36: A Journey into Number Patterns and Mathematical Concepts
This sequence, 1, 4, 9, 16, 25, 36..., is more than just a list of numbers; it's a gateway to understanding fundamental mathematical concepts, from basic arithmetic to more advanced ideas. This article will delve deep into this seemingly simple sequence, exploring its underlying patterns, revealing its connection to other mathematical fields, and highlighting its significance in various applications. We'll explore its generation, its relation to geometry, its place within algebra, and even touch upon its relevance in computer science. Prepare to be amazed by the richness hidden within this seemingly simple progression.
Understanding the Pattern: The Square Numbers
The most immediate observation about the sequence 1, 4, 9, 16, 25, 36... is that each number is a perfect square. A perfect square is a number that can be obtained by squaring (multiplying by itself) an integer. Let's break it down:
- 1 = 1² (1 multiplied by 1)
- 4 = 2² (2 multiplied by 2)
- 9 = 3² (3 multiplied by 3)
- 16 = 4² (4 multiplied by 4)
- 25 = 5² (5 multiplied by 5)
- 36 = 6² (6 multiplied by 6)
This simple observation forms the foundation of our understanding of this sequence. It's a sequence of square numbers, where each term is the square of its position in the sequence. The nth term in the sequence is simply n². This elegant formula allows us to predict any term in the sequence, no matter how far along it goes. Want to know the 100th term? It's 100² = 10,000.
Visualizing the Pattern: Geometric Representation
The beauty of this sequence isn't limited to its algebraic representation. It also has a compelling geometric interpretation. Each number in the sequence can be represented visually as a square arrangement of dots or units.
- 1: A single dot forms a 1x1 square.
- 4: Four dots can be arranged in a 2x2 square.
- 9: Nine dots form a 3x3 square.
- 16: Sixteen dots form a 4x4 square.
- And so on...
This geometric representation provides a powerful visual aid for understanding the concept of square numbers. It allows for a tangible connection between the abstract mathematical idea and a concrete visual form. This visual approach is particularly helpful for learners who benefit from concrete examples and spatial reasoning.
Exploring the Sequence Algebraically: Generating the Terms
We've already touched upon the algebraic formula for generating the terms in the sequence: n². This formula is exceptionally concise and elegant. It's a testament to the power of mathematical notation to capture complex patterns succinctly.
Beyond the simple n² formula, we can also explore other algebraic approaches to representing the sequence. For instance, we could represent the sequence using recursive formulas. A recursive formula defines a term based on the previous terms. While not as elegant as the explicit formula, a recursive approach offers a different perspective on the sequence's structure. A simple (though less efficient) recursive formula could be:
- a<sub>1</sub> = 1
- a<sub>n</sub> = a<sub>n-1</sub> + 2n - 1 (for n > 1)
This formula states that each term is obtained by adding an odd number to the previous term. The odd number added increases by 2 with each subsequent term.
Connections to Other Mathematical Concepts: Differences and Sums
Let's analyze the differences between consecutive terms in the sequence:
- 4 - 1 = 3
- 9 - 4 = 5
- 16 - 9 = 7
- 25 - 16 = 9
- 36 - 25 = 11
Notice a pattern? The differences form a sequence of consecutive odd numbers. This observation provides further insight into the structure of the square numbers. The difference between consecutive square numbers always increases by 2.
Now let's consider the sums of the sequence:
- 1 = 1
- 1 + 4 = 5
- 1 + 4 + 9 = 14
- 1 + 4 + 9 + 16 = 30
- 1 + 4 + 9 + 16 + 25 = 55
- 1 + 4 + 9 + 16 + 25 + 36 = 91
The sums themselves don’t immediately reveal a simple pattern like the differences. However, the sums of square numbers are connected to another important mathematical concept – the sum of cubes and sums of consecutive integers. The formula for the sum of the first n square numbers is given by: n(n+1)(2n+1)/6. This formula highlights a link between the sequence of square numbers and the theory of summation.
Applications in Various Fields: From Physics to Computer Science
The sequence of square numbers isn't just a theoretical curiosity; it has practical applications in various fields:
-
Physics: In kinematics, the distance traveled by an object under constant acceleration is related to the square of the time elapsed. The formula d = 1/2at², where 'a' is acceleration and 't' is time, showcases the square function in action.
-
Computer Science: In algorithms and data structures, the time complexity of certain algorithms (like nested loops) is often expressed in terms of square functions (O(n²)). Understanding square numbers is crucial for analyzing the efficiency of such algorithms.
-
Geometry: As discussed earlier, the visual representation of square numbers as square grids directly connects this sequence to geometric concepts. This is foundational in areas like calculating areas and volumes of simple shapes.
-
Statistics: The concept of variance and standard deviation in statistics involves squaring differences from the mean, which brings the square function to the forefront in data analysis.
Frequently Asked Questions (FAQs)
Q1: Is this the only sequence of perfect squares?
A1: No, this sequence specifically refers to the sequence of the squares of the natural numbers (1, 2, 3, 4...). You could, however, create sequences of squares of other number sets, like even numbers (4, 16, 36...) or odd numbers (1, 9, 25...).
Q2: What is the formula for the sum of the first n square numbers?
A2: The formula for the sum of the first n square numbers is: n(n+1)(2n+1)/6
Q3: How can I find the nth term of the sequence quickly?
A3: Simply square the value of 'n'. The nth term is always n².
Q4: Are there any other interesting patterns hidden within this sequence?
A4: Yes! The differences between consecutive terms form a sequence of consecutive odd numbers, and the sums of the terms relate to more complex summation formulas. Exploration into these relationships can lead to a richer mathematical understanding.
Q5: How does this sequence relate to other mathematical sequences?
A5: The sequence of square numbers has connections to other sequences like the sequence of odd numbers (as seen in the differences between consecutive terms) and sequences related to summation formulas. The study of these relationships illuminates deep connections within mathematics.
Conclusion: A Simple Sequence, Profound Implications
The seemingly simple sequence 1, 4, 9, 16, 25, 36... is a powerful illustration of how seemingly simple mathematical concepts can lead to profound insights. By exploring its underlying patterns, both geometrically and algebraically, we've uncovered its connections to various mathematical fields and its applicability in diverse areas. This journey highlights the beauty and interconnectedness of mathematics, encouraging a deeper appreciation for the patterns and structures that govern our world. The exploration doesn't end here; further investigation into related mathematical concepts will only enhance your understanding and appreciation of this fundamental sequence. The world of numbers is vast and full of exciting discoveries waiting to be made.
Latest Posts
Latest Posts
-
Which Graph Represents A Function With An Initial Value Of
Sep 23, 2025
-
How Do You Say Ice Cream In German
Sep 23, 2025
-
60 Of What Number Is 30
Sep 23, 2025
-
Practice Problems Limiting And Excess Reagents
Sep 23, 2025
-
Cross Sections Perpendicular To The X Axis
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 4 9 16 25 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.