1 3x Y 4 Solve For Y
faraar
Sep 22, 2025 · 5 min read
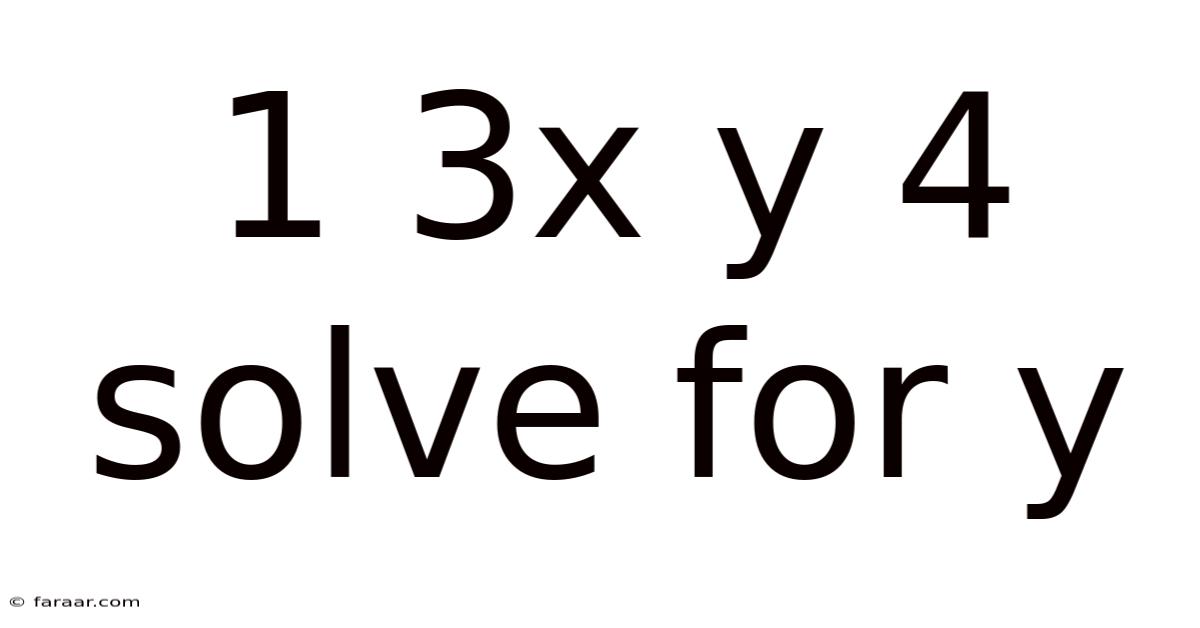
Table of Contents
Solving for y: A Comprehensive Guide to 13x + y = 4
This article provides a comprehensive guide on how to solve the equation 13x + y = 4 for y. We'll explore the algebraic steps involved, delve into the underlying mathematical concepts, and examine various approaches to understanding and solving this type of equation. We will also address frequently asked questions and provide additional examples to solidify your understanding. Understanding how to isolate variables is a fundamental skill in algebra, and this equation serves as an excellent example to master this crucial concept.
Introduction: Understanding Linear Equations
The equation 13x + y = 4 is a linear equation in two variables, x and y. A linear equation represents a straight line when graphed on a coordinate plane. The goal of solving for y is to isolate y on one side of the equation, expressing it in terms of x. This allows us to determine the value of y for any given value of x. This process is fundamental to understanding linear relationships and their applications in various fields like physics, economics, and computer science.
Step-by-Step Solution: Isolating y
To solve 13x + y = 4 for y, we need to manipulate the equation algebraically to isolate y. This involves performing the same operation on both sides of the equation to maintain balance. Here's a step-by-step breakdown:
-
Identify the term involving y: In the equation 13x + y = 4, the term involving y is simply y.
-
Isolate the y term: To isolate the y term, we need to move the 13x term to the right-hand side of the equation. We can achieve this by subtracting 13x from both sides:
13x + y - 13x = 4 - 13x
This simplifies to:
y = 4 - 13x
-
Rewrite the equation: The solution for y is now expressed in terms of x:
y = -13x + 4
This equation shows that the value of y depends on the value of x. For every value of x, there's a corresponding value of y that satisfies the original equation.
Graphical Representation: Visualizing the Solution
The equation y = -13x + 4 represents a straight line on a coordinate plane. The slope of this line is -13 (the coefficient of x), and the y-intercept is 4 (the constant term). The slope indicates the steepness of the line, and the y-intercept represents the point where the line intersects the y-axis (where x = 0). Graphing this line helps visualize the relationship between x and y, showing all possible solutions to the original equation.
Understanding the Concepts: Inverse Operations
The process of solving for y involves using inverse operations. Addition and subtraction are inverse operations, as are multiplication and division. In our example, we used subtraction (the inverse of addition) to isolate the y term. If the equation involved multiplication or division with y, we would use division or multiplication, respectively, as the inverse operation.
For instance, if the equation were 2y = 8, we would divide both sides by 2 to solve for y:
2y / 2 = 8 / 2 => y = 4
Similarly, if the equation were y/3 = 5, we would multiply both sides by 3:
(y/3) * 3 = 5 * 3 => y = 15
Solving Similar Equations: Practicing Your Skills
Let's practice solving a few more equations similar to 13x + y = 4. Understanding the underlying principles is crucial for tackling more complex algebraic problems.
Example 1: 5x + y = 10
Subtracting 5x from both sides, we get:
y = 10 - 5x
Example 2: -2x + y = 7
Adding 2x to both sides, we get:
y = 7 + 2x or y = 2x + 7
Example 3: y - 6x = 12
Adding 6x to both sides, we get:
y = 12 + 6x or y = 6x + 12
These examples demonstrate the consistent application of inverse operations to isolate the variable y. The key is to perform the same operation on both sides of the equation to maintain equality.
Advanced Concepts: Systems of Linear Equations
Understanding how to solve for a single variable in a linear equation is a crucial stepping stone to solving systems of linear equations. A system of linear equations involves two or more equations with two or more variables. Solving these systems often involves techniques like substitution or elimination, where you might solve for one variable in one equation and substitute its expression into another equation. The solution to a system of linear equations represents the point(s) where the lines intersect on a graph.
Frequently Asked Questions (FAQ)
Q1: What if the equation was more complex, like 13x + 2y = 4?
A1: In this case, you'd need to first isolate the term with 'y' and then divide to solve for y. First, subtract 13x from both sides: 2y = 4 - 13x. Then, divide both sides by 2: y = (4 - 13x)/2 or y = 2 - (13/2)x
Q2: Can x have any value?
A2: Yes, x can be any real number. The equation y = -13x + 4 defines a function where for each value of x, there is a corresponding value of y.
Q3: What does it mean to "solve" an equation?
A3: Solving an equation means finding the values of the variables that make the equation true. In this case, solving for y means expressing y in terms of x, so that for any given x, you can find the corresponding y that satisfies the equation.
Q4: What are some real-world applications of solving linear equations?
A4: Linear equations are used extensively in various fields. For instance, in physics, they can model motion, in economics, they can model supply and demand, and in computer science, they're used in algorithms and data analysis.
Conclusion: Mastering the Fundamentals
Solving the equation 13x + y = 4 for y, resulting in y = -13x + 4, is a fundamental algebraic skill. Understanding the step-by-step process of isolating variables, using inverse operations, and visualizing the solution graphically are essential for progressing to more advanced mathematical concepts. The ability to manipulate equations effectively is a cornerstone of success in various scientific and technical fields. Remember to practice regularly to solidify your understanding and build confidence in your problem-solving abilities. By mastering these fundamental concepts, you’ll build a strong foundation for tackling more complex algebraic problems and expanding your mathematical knowledge. The seemingly simple equation 13x + y = 4 opens doors to a deeper understanding of algebra and its wide-ranging applications.
Latest Posts
Latest Posts
-
Find The Length Of Arc Ab
Sep 22, 2025
-
What Is The Formula For Iron Ii Chloride
Sep 22, 2025
-
Which Expression Represents The Perimeter Of The Triangle
Sep 22, 2025
-
Is Nabro3 An Acid Or Base
Sep 22, 2025
-
How To Find The Revenue Function
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 3x Y 4 Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.