1 2 1 4 1 4
faraar
Sep 16, 2025 · 6 min read
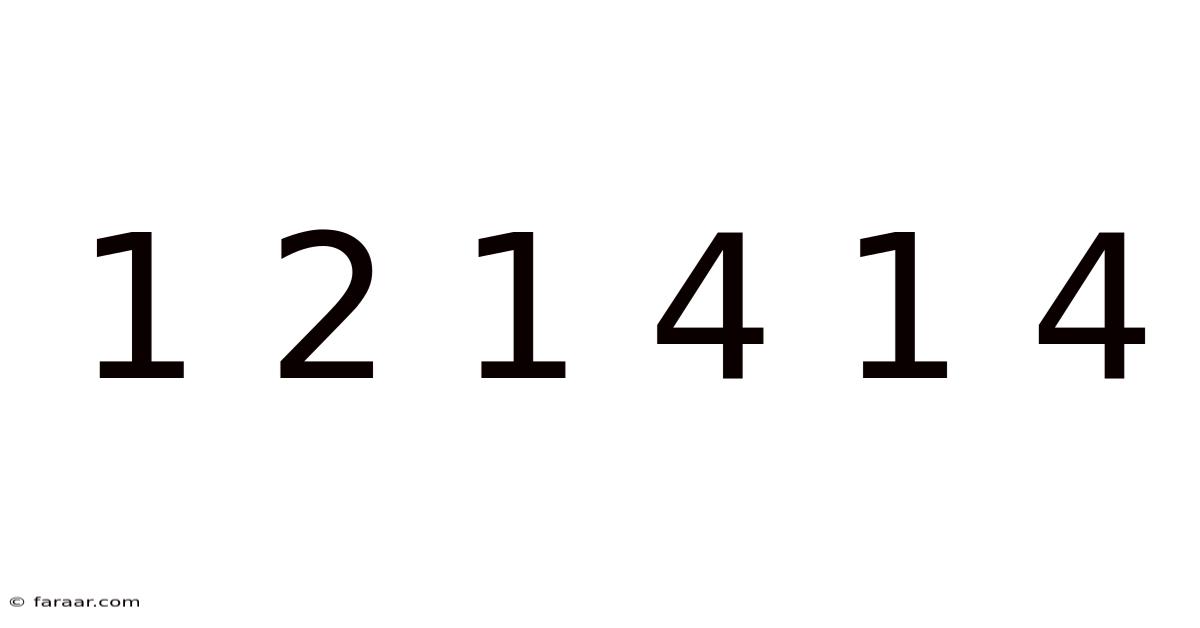
Table of Contents
Unlocking the Mystery of 1 2 1 4 1 4: A Deep Dive into Number Sequences and Mathematical Patterns
The seemingly simple sequence "1 2 1 4 1 4" might initially appear random, but a closer examination reveals a fascinating interplay of mathematical concepts, pattern recognition, and even potential links to other fields like music and coding. This article will delve into the various interpretations of this sequence, exploring its potential origins, underlying logic, and broader implications within the world of mathematics and beyond. Understanding this seemingly simple sequence can unlock a deeper appreciation for the beauty and elegance hidden within numerical patterns.
Understanding Number Sequences: A Foundation
Before we tackle the specific sequence "1 2 1 4 1 4," it's crucial to understand the broader context of number sequences. These are ordered lists of numbers, often following a specific rule or pattern. Some common types include:
- Arithmetic sequences: Each term is obtained by adding a constant value (the common difference) to the previous term (e.g., 1, 4, 7, 10...).
- Geometric sequences: Each term is obtained by multiplying the previous term by a constant value (the common ratio) (e.g., 2, 6, 18, 54...).
- Fibonacci sequence: Each term is the sum of the two preceding terms (e.g., 1, 1, 2, 3, 5, 8...).
- Look-and-say sequence: Each term describes the previous term (e.g., 1, 11, 21, 1211, 111221...).
Our sequence, "1 2 1 4 1 4," doesn't immediately fit into any of these established categories. This suggests a more nuanced or potentially unique pattern requiring further investigation.
Possible Interpretations of 1 2 1 4 1 4
The lack of an immediately obvious pattern opens up avenues for multiple interpretations, depending on the assumed rules or underlying structure. Let's explore some possibilities:
1. A Repeated Pattern: The most straightforward interpretation is to see the sequence as a repetition of the sub-sequence "1 2 1 4." This implies a simple repeating pattern, but it lacks an inherent mathematical function or generation rule. While simple, this interpretation highlights the potential for seemingly complex sequences to arise from very basic repetitions. This simplicity itself could be significant in certain applications, particularly in signal processing or data compression where repeated patterns are readily exploited.
2. A Transformation Sequence: We could consider this sequence as the result of applying a specific transformation rule to a prior sequence. For instance, each number might represent a transformation applied to a base set, but without knowing the base set or transformation, this remains purely speculative. The lack of a clear transformation function makes this a less concrete interpretation compared to the repeated pattern.
3. A Code or Cipher: Looking beyond purely mathematical interpretations, it's possible that "1 2 1 4 1 4" is a coded message. This requires establishing a key or a decryption method. Without additional information or context, deciphering it becomes a matter of speculation. The numbers could represent letters (using A=1, B=2, etc.), musical notes, or symbols within a specific system. This interpretation underscores the potential for sequences like this to have meaning outside the realm of pure mathematics.
4. A Basis for a Recursive Function: A more advanced interpretation might involve constructing a recursive function that generates this sequence or an extension of it. A recursive function calls itself within its own definition, creating a self-similar structure. The design of such a function would require careful consideration of the sequence’s characteristics and the desired behavior of the function. This approach moves beyond simple pattern recognition into the creation of algorithms and potentially more complex mathematical structures.
Exploring Potential Links to Other Fields
Beyond pure mathematics, the sequence "1 2 1 4 1 4" could hold relevance in several other fields:
1. Music Theory: Number sequences are frequently used in music composition and analysis. The sequence could represent rhythmic patterns, note durations, or intervals in a musical piece. Further research could explore whether this sequence corresponds to any existing musical motif or pattern. The rhythmic possibilities alone warrant further investigation.
2. Computer Science and Coding: In programming, sequences of numbers are often used to index arrays or represent data structures. The sequence could be a part of an algorithm, a data encoding scheme, or even part of a cryptographic key. The significance would entirely depend on the application and context.
3. Cryptography: As mentioned earlier, the sequence could form part of a more complex cipher. The length of the sequence (six digits) suggests it might be a component of a larger key or encryption algorithm. However, the apparent lack of readily apparent mathematical structure makes this a less likely interpretation without additional context.
Mathematical Analysis and Pattern Extension
Even without a definitive generating rule, we can attempt to analyze the sequence further. Could it be extended? What would a potential extension look like?
A simple extension, based on the repeated pattern interpretation, would be "1 2 1 4 1 4 1 2 1 4 1 4...". However, this is purely speculative. More sophisticated approaches would involve exploring potential recursive relationships, trying to find underlying functions, or using statistical methods to identify underlying distributions.
For example, we could consider calculating the mean, median, mode, and standard deviation of the sequence to gauge its statistical properties. This provides quantitative insights that might help to understand the sequence better, even if it doesn't unveil a direct generating rule.
Frequently Asked Questions (FAQ)
-
Q: Is there a definitive mathematical formula to generate this sequence? A: Currently, there is no definitively proven formula. The interpretations presented above are possibilities, but none have been conclusively validated.
-
Q: Could this sequence be related to other known mathematical sequences? A: At present, no direct relationship to well-known sequences like the Fibonacci sequence or other standard arithmetic or geometric progressions has been established.
-
Q: What is the significance of this sequence? A: The significance is not intrinsically inherent to the sequence itself. Its meaning depends entirely on the context in which it appears. Its simplicity could be significant in some contexts, while its lack of obvious pattern makes it intriguing in others.
Conclusion: A Journey of Exploration
The seemingly simple sequence "1 2 1 4 1 4" presents a compelling case study in mathematical pattern recognition and the diverse ways we can approach and interpret numerical data. While a definitive, universally accepted explanation remains elusive, exploring its potential interpretations, investigating its links to other fields, and considering potential extensions has expanded our understanding of the rich possibilities hidden within numerical patterns. This sequence serves as a reminder that even the most seemingly basic mathematical structures can hold a wealth of intriguing possibilities, encouraging further exploration and a deeper appreciation for the multifaceted nature of mathematics. Future research, possibly involving advanced statistical methods or computational analysis, might unlock a more profound understanding of this seemingly simple, yet enigmatic, sequence.
Latest Posts
Latest Posts
-
Compute The Height Of The Uniform Distribution
Sep 16, 2025
-
A 1 2h B1 B2 Solve For B2
Sep 16, 2025
-
A Triangle Is Dilated By A Scale Factor Of 1 2
Sep 16, 2025
-
How To Dilate On A Coordinate Plane
Sep 16, 2025
-
Write The Sentence As An Equation
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1 2 1 4 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.