A 1 2h B1 B2 Solve For B2
faraar
Sep 16, 2025 · 5 min read
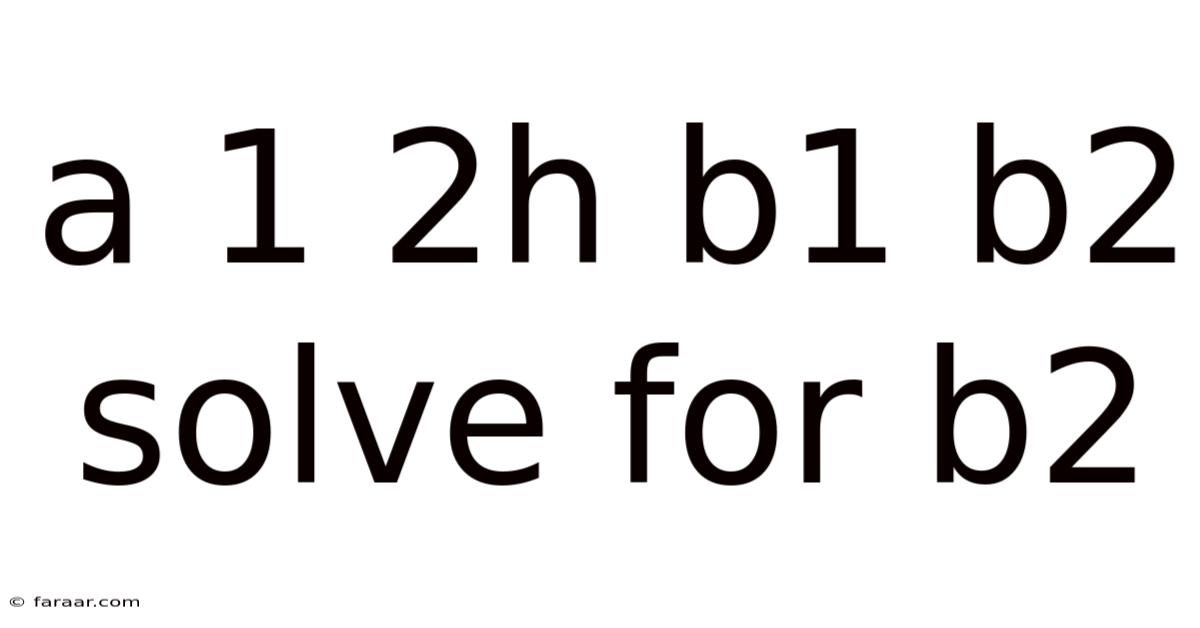
Table of Contents
Solving for b₂ in a 1/2hb₁ + b₂ Equation: A Comprehensive Guide
Understanding how to solve for a specific variable within an equation is a fundamental skill in algebra. This article provides a comprehensive guide on solving for b₂ in the equation 1/2h(b₁ + b₂), focusing on different approaches and offering detailed explanations to aid comprehension. We'll explore the equation's context, break down the solution step-by-step, and address frequently asked questions. This detailed explanation will equip you with the confidence to tackle similar algebraic problems.
Understanding the Equation: Area of a Trapezoid
The equation 1/2h(b₁ + b₂) represents the formula for calculating the area (A) of a trapezoid. Let's define the variables:
- A: Represents the area of the trapezoid. This is the value we often want to find or use in calculations.
- h: Represents the height of the trapezoid – the perpendicular distance between the two parallel bases.
- b₁: Represents the length of one of the parallel bases of the trapezoid.
- b₂: Represents the length of the other parallel base of the trapezoid.
The equation is typically written as: A = 1/2h(b₁ + b₂)
Our goal is to isolate b₂, meaning we want to rearrange the equation so that b₂ is on one side of the equation and all other variables are on the other.
Step-by-Step Solution for b₂
Let's break down the process of solving for b₂ in a systematic way:
Step 1: Multiply both sides by 2
To eliminate the fraction 1/2, we multiply both sides of the equation by 2:
2A = h(b₁ + b₂)
Step 2: Distribute 'h'
The next step involves distributing the 'h' to both terms inside the parentheses:
2A = hb₁ + hb₂
Step 3: Subtract hb₁ from both sides
Our goal is to isolate the term containing b₂. To do this, we subtract 'hb₁' from both sides of the equation:
2A - hb₁ = hb₂
Step 4: Divide both sides by 'h'
Finally, to isolate b₂, we divide both sides of the equation by 'h':
(2A - hb₁) / h = b₂
Therefore, the solution for b₂ is:
b₂ = (2A - hb₁) / h
This equation now allows you to calculate the length of one base (b₂) of a trapezoid if you know its area (A), height (h), and the length of the other base (b₁).
Illustrative Example
Let's solidify our understanding with a practical example. Suppose a trapezoid has an area (A) of 30 square units, a height (h) of 6 units, and one base (b₁) of 3 units. Let's find the length of the other base (b₂):
- Substitute the known values: b₂ = (2 * 30 - 6 * 3) / 6
- Simplify the equation: b₂ = (60 - 18) / 6
- Perform the calculation: b₂ = 42 / 6
- Final Result: b₂ = 7 units
Therefore, the length of the other base (b₂) is 7 units.
Alternative Approaches and Considerations
While the steps outlined above are the most straightforward approach, there are alternative ways to solve for b₂. The choice of method often depends on personal preference and the complexity of the problem.
-
Solving using inverse operations: The steps above can also be viewed as a sequence of inverse operations. We undo the operations performed on b₂ in reverse order. First, we undo the addition by subtracting, then we undo the multiplication by dividing.
-
Factoring: While less intuitive for this specific equation, factoring can be a useful technique in more complex algebraic expressions.
Potential Challenges and Troubleshooting
Students sometimes encounter challenges when working with algebraic equations. Here are some common issues and how to overcome them:
-
Order of operations (PEMDAS/BODMAS): Remember the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). Incorrect order can lead to inaccurate results.
-
Working with fractions: Ensure you are comfortable manipulating fractions. Remember that multiplying by 2 is the inverse of dividing by 1/2.
-
Negative numbers: Be mindful of the rules for working with negative numbers, especially when subtracting or dividing.
-
Checking your work: After solving for b₂, always check your answer by substituting the values back into the original equation (A = 1/2h(b₁ + b₂)). If both sides of the equation are equal, your solution is correct.
Frequently Asked Questions (FAQ)
Q1: What if 'h' is zero?
If the height ('h') of the trapezoid is zero, the equation becomes undefined because division by zero is not allowed in mathematics. A trapezoid with zero height doesn't exist geometrically.
Q2: Can b₁ and b₂ be negative values?
In the context of the area of a trapezoid, b₁ and b₂ represent lengths, which are always positive values. Therefore, negative values for b₁ and b₂ are not physically meaningful in this context.
Q3: How does this equation relate to other geometric formulas?
The trapezoid area formula is related to other geometric formulas, such as the area of a rectangle (A = lw) and a triangle (A = 1/2bh). Notice the similarity – they all involve multiplying base(s) and height.
Q4: What if I have a more complex equation involving b₂?
If the equation is significantly more complex, consider using techniques like factoring, completing the square, or the quadratic formula (if it is a quadratic equation) to solve for b₂. Systematic application of algebraic rules remains key.
Q5: What are some real-world applications of this equation?
The trapezoid area formula has many real-world applications in fields such as civil engineering (calculating land areas), architecture (designing buildings with trapezoidal shapes), and surveying (measuring land plots).
Conclusion
Solving for b₂ in the equation A = 1/2h(b₁ + b₂) is a fundamental algebraic exercise with practical applications in geometry and various fields. By understanding the steps involved and practicing with examples, you can confidently tackle this and similar problems. Remember the importance of understanding the underlying concepts, applying the correct order of operations, and always checking your work to ensure accuracy. This comprehensive guide aims to not only provide a solution but also build your understanding and problem-solving skills in algebra. With consistent practice, you will become proficient in solving for variables in various equations.
Latest Posts
Latest Posts
-
Is Lino3 Acidic Basic Or Neutral
Sep 16, 2025
-
Two Reactions And Their Equilibrium Constants Are Given
Sep 16, 2025
-
What Does It Mean When You See In A Cell
Sep 16, 2025
-
Determine The Solution For X2 36 12x
Sep 16, 2025
-
What Is The Measure Of Def
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about A 1 2h B1 B2 Solve For B2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.